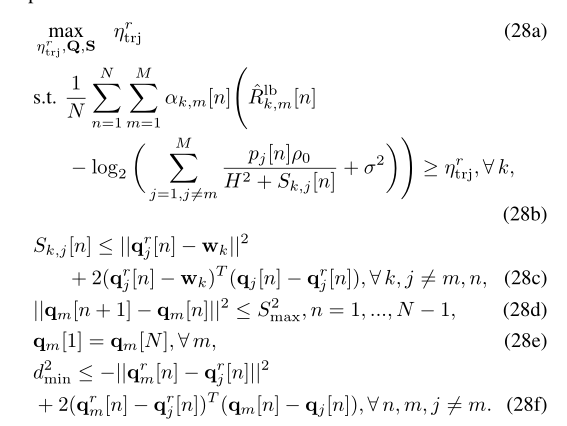
how to deal with this problem?
In this problem ,s[n] is located in denominator,cvx tells me that {positive constant} ./ {real affine},
s[n] is variable.
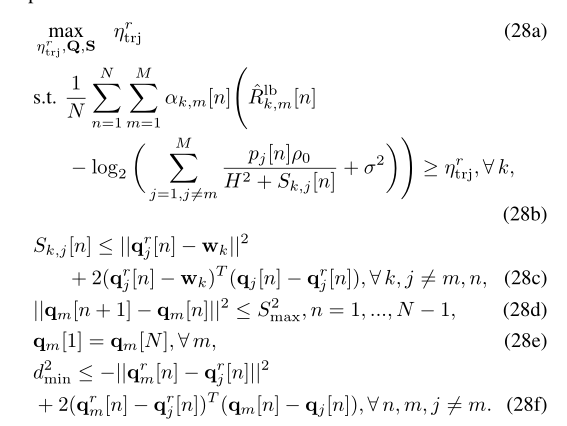
how to deal with this problem?
In this problem ,s[n] is located in denominator,cvx tells me that {positive constant} ./ {real affine},
s[n] is variable.
You can adapt the solution at How to express log(sum(xi)) in CVX .
Hello, my situation and log_ sum_ Inv is different. I need to subtract a value(j!=m)In this case, can it be solved by your method?
Yes, I believe it can.
Dear Mark ,hello
eta_tra(1)<=sum(a1(:,1).*(R_lb_11-log(t2(:,1))./log(2)))+sum(a2(:,1).*(R_lb_21-log(t1(:,1))./log(2)));
eta_tra(2)<=sum(a1(:,2).*(R_lb_12-log(t2(:,2))./log(2)))+sum(a2(:,2).*(R_lb_22-log(t1(:,2))./log(2)));
eta_tra(3)<=sum(a1(:,3).*(R_lb_13-log(t2(:,3))./log(2)))+sum(a2(:,3).*(R_lb_23-log(t1(:,3))./log(2)));
eta_tra(4)<=sum(a1(:,4).*(R_lb_14-log(t2(:,4))./log(2)))+sum(a2(:,4).*(R_lb_24-log(t1(:,4))./log(2)));
eta_tra(5)<=sum(a1(:,5).*(R_lb_15-log(t2(:,5))./log(2)))+sum(a2(:,5).*(R_lb_25-log(t1(:,5))./log(2)));
eta_tra(6)<=sum(a1(:,6).*(R_lb_16-log(t2(:,6))./log(2)))+sum(a2(:,6).*(R_lb_26-log(t1(:,6))./log(2)));
t1>=log_sum_exp(log(N0),y1);
t2>=log_sum_exp(log(N0),y2);
(H.^2+S2)./(p2.*rou)>=exp(-y2);
(H.^2+S1)./(p1.*rou)>=exp(-y1);
I have a problem according to your method
Illegal operation: {concave} - {concave}
Error test (line 437)
eta_ tra(1)<=sum(a1(:,1).* (R_lb_11-log(t2(:,1))./ log(2)))+sum(a2(:,1).* (R_lb_21-log(t1(:,1))./ log(2)));
Don’t sum over all terms, then subtract one of those terms (j = m). The sum should not include the j = m term to begin with,
For example: log(x1)+log(x3) is accepted by CVX. But log(x1)+log(x2)+log(x3)-log(x2) is not accepted by CVX.
I didn’t subtract the term (j=m). I assumed that M=2, and there was only one opposite term of j at a time. Therefore, there was only one t in (log_sum_exp). After CVX was run, it was {concave} - {concave}. Thank you for your answer. Now I don’t know why this error occurred.
Can you provide a reproducible example, complete with all code and input data?
Trajectory optimization problem, power P is known, wk is the target position is known, Rho_ 0. It is known that Q is the best trajectory to be solved. I initialize a trajectory and iterate the trajectory. In the expression, yital (eta_tra in Matlab), s and Q are variables, R_ lb_ Km is the erexpressions obtained from Q。
cvx_begin
variables q1_tra(N,2) q2_tra(N,2) S1(N,6) S2(N,6) eta_tra(K,1) t1(N,6) y1(N,6) t2(N,6) y2(N,6)
expressions R_lb_11(N,1) R_lb_12(N,1) R_lb_13(N,1) R_lb_14(N,1) R_lb_15(N,1) R_lb_16(N,1) R_lb_21(N,1) R_lb_22(N,1) R_lb_23(N,1) R_lb_24(N,1) R_lb_25(N,1) R_lb_26(N,1)
for tt=1:N
n=tt;
R_lb_11(n)=-A_11(n).((q1_tra(n,1)-q(1,1)).^2+(q1_tra(n,2)-q(1,2)).^2-norm(q1(n,:)-q(1,:)).^2)-A_21(n).((q2_tra(n,1)-q(1,1)).^2+(q2_tra(n,2)-q(1,2)).^2-norm(q2(n,:)-q(1,:)).^2)+B_11(n);
R_lb_12(n)=-A_12(n).((q1_tra(n,1)-q(2,1)).^2+(q1_tra(n,2)-q(2,2)).^2-norm(q1(n,:)-q(2,:)).^2)-A_22(n).((q2_tra(n,1)-q(2,1)).^2+(q2_tra(n,2)-q(2,2)).^2-norm(q2(n,:)-q(2,:)).^2)+B_12(n);
R_lb_13(n)=-A_13(n).((q1_tra(n,1)-q(3,1)).^2+(q1_tra(n,2)-q(3,2)).^2-norm(q1(n,:)-q(3,:)).^2)-A_23(n).((q2_tra(n,1)-q(3,1)).^2+(q2_tra(n,2)-q(3,2)).^2-norm(q2(n,:)-q(3,:)).^2)+B_13(n);
R_lb_14(n)=-A_14(n).((q1_tra(n,1)-q(4,1)).^2+(q1_tra(n,2)-q(4,2)).^2-norm(q1(n,:)-q(4,:)).^2)-A_24(n).((q2_tra(n,1)-q(4,1)).^2+(q2_tra(n,2)-q(4,2)).^2-norm(q2(n,:)-q(4,:)).^2)+B_14(n);
R_lb_15(n)=-A_15(n).((q1_tra(n,1)-q(5,1)).^2+(q1_tra(n,2)-q(5,2)).^2-norm(q1(n,:)-q(5,:)).^2)-A_25(n).((q2_tra(n,1)-q(5,1)).^2+(q2_tra(n,2)-q(5,2)).^2-norm(q2(n,:)-q(5,:)).^2)+B_15(n);
R_lb_16(n)=-A_16(n).((q1_tra(n,1)-q(6,1)).^2+(q1_tra(n,2)-q(6,2)).^2-norm(q1(n,:)-q(6,:)).^2)-A_26(n).((q2_tra(n,1)-q(6,1)).^2+(q2_tra(n,2)-q(6,2)).^2-norm(q2(n,:)-q(6,:)).^2)+B_16(n);
R_lb_21(n)=-A_11(n).*((q1_tra(n,1)-q(1,1)).^2+(q1_tra(n,2)-q(1,2)).^2-norm(q1(n,:)-q(1,:)).^2)-A_21(n).*((q2_tra(n,1)-q(1,1)).^2+(q2_tra(n,2)-q(1,2)).^2-norm(q2(n,:)-q(1,:)).^2)+B_11(n);
R_lb_22(n)=-A_12(n).*((q1_tra(n,1)-q(2,1)).^2+(q1_tra(n,2)-q(2,2)).^2-norm(q1(n,:)-q(2,:)).^2)-A_22(n).*((q2_tra(n,1)-q(2,1)).^2+(q2_tra(n,2)-q(2,2)).^2-norm(q2(n,:)-q(2,:)).^2)+B_12(n);
R_lb_23(n)=-A_13(n).*((q1_tra(n,1)-q(3,1)).^2+(q1_tra(n,2)-q(3,2)).^2-norm(q1(n,:)-q(3,:)).^2)-A_23(n).*((q2_tra(n,1)-q(3,1)).^2+(q2_tra(n,2)-q(3,2)).^2-norm(q2(n,:)-q(3,:)).^2)+B_13(n);
R_lb_24(n)=-A_14(n).*((q1_tra(n,1)-q(4,1)).^2+(q1_tra(n,2)-q(4,2)).^2-norm(q1(n,:)-q(4,:)).^2)-A_24(n).*((q2_tra(n,1)-q(4,1)).^2+(q2_tra(n,2)-q(4,2)).^2-norm(q2(n,:)-q(4,:)).^2)+B_14(n);
R_lb_25(n)=-A_15(n).*((q1_tra(n,1)-q(5,1)).^2+(q1_tra(n,2)-q(5,2)).^2-norm(q1(n,:)-q(5,:)).^2)-A_25(n).*((q2_tra(n,1)-q(5,1)).^2+(q2_tra(n,2)-q(5,2)).^2-norm(q2(n,:)-q(5,:)).^2)+B_15(n);
R_lb_26(n)=-A_16(n).*((q1_tra(n,1)-q(6,1)).^2+(q1_tra(n,2)-q(6,2)).^2-norm(q1(n,:)-q(6,:)).^2)-A_26(n).*((q2_tra(n,1)-q(6,1)).^2+(q2_tra(n,2)-q(6,2)).^2-norm(q2(n,:)-q(6,:)).^2)+B_16(n);
end
obj_value=0;
for k=1:K
obj_value=obj_value+eta_tra(k);
end
maximize(obj_value);
subject to
eta_tra(1)<=sum(a1(:,1).*(R_lb_11-log(t2(:,1))./log(2)))+sum(a2(:,1).*(R_lb_21-log(t1(:,1))./log(2)));
eta_tra(2)<=sum(a1(:,2).*(R_lb_12-log(t2(:,2))./log(2)))+sum(a2(:,2).*(R_lb_22-log(t1(:,2))./log(2)));
eta_tra(3)<=sum(a1(:,3).*(R_lb_13-log(t2(:,3))./log(2)))+sum(a2(:,3).*(R_lb_23-log(t1(:,3))./log(2)));
eta_tra(4)<=sum(a1(:,4).*(R_lb_14-log(t2(:,4))./log(2)))+sum(a2(:,4).*(R_lb_24-log(t1(:,4))./log(2)));
eta_tra(5)<=sum(a1(:,5).*(R_lb_15-log(t2(:,5))./log(2)))+sum(a2(:,5).*(R_lb_25-log(t1(:,5))./log(2)));
eta_tra(6)<=sum(a1(:,6).*(R_lb_16-log(t2(:,6))./log(2)))+sum(a2(:,6).*(R_lb_26-log(t1(:,6))./log(2)));
t1>=log_sum_exp(log(N0),y1);
t2>=log_sum_exp(log(N0),y2);
(H.^2+S2)./(p2.*rou)>=exp(-y2);
(H.^2+S1)./(p1.*rou)>=exp(-y1);That’s not a reproducible example. It is missing the input data. You should make the example as small and simple as you can, while still illustrating the error. That is for everyone’s benefit, including your own.
You shouldn’t be taking log of t2. Rather, t2 takes the place of the log_sum_inv. Please study section 5.2.7 of https://docs.mosek.com/modeling-cookbook/expo.html#modeling-with-the-exponential-cone and see example CVX code at Log( {convex} ) . The only log term you should have should be of a constant, not a CvX variable or expression.
Thank you, brother Mark. I’ll study it carefully
Dear Mark
What is the reason for this situation after my modification?
eta_tra(1)<=sum(a1(:,1).(R_lb_11-t2(:,1)./log(2)))+sum(a2(:,1).(R_lb_21-t1(:,1)./log(2)));
eta_tra(2)<=sum(a1(:,2).(R_lb_12-t2(:,2)./log(2)))+sum(a2(:,2).(R_lb_22-t1(:,2)./log(2)));
eta_tra(3)<=sum(a1(:,3).(R_lb_13-t2(:,3)./log(2)))+sum(a2(:,3).(R_lb_23-t1(:,3)./log(2)));
eta_tra(4)<=sum(a1(:,4).(R_lb_14-t2(:,4)./log(2)))+sum(a2(:,4).(R_lb_24-t1(:,4)./log(2)));
eta_tra(5)<=sum(a1(:,5).(R_lb_15-t2(:,5)./log(2)))+sum(a2(:,5).(R_lb_25-t1(:,5)./log(2)));
eta_tra(6)<=sum(a1(:,6).(R_lb_16-t2(:,6)./log(2)))+sum(a2(:,6).(R_lb_26-t1(:,6)./log(2)));
You may have bad numerical scaling.
In any event, if you have Mosek available, use that as solver. Otherwise, follow the advice in CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions
Brother Mark, I installed MOSEK. There is no problem inputting mosekopt. Why is there no MOSEK in CVX solver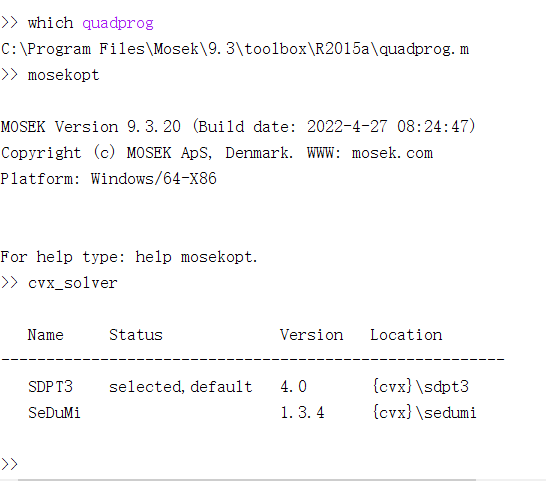
Try re-installing CVX. Hopefully it will find Mosek.
If not,
Have you set the MATLAB path correctly?
What is the output of mosekdiag ?
This is the result of mosekdiag. There is an error. I try to reinstall CVX