Is your lMosek license in the right place? Have you tried a new MATLAB session? Get mosekdiag to give a favorable result. Then reinstall CVX.
Thank you very much for Mark’s clarification. MOSEK is already available
So does everything work now?
The result is no longer Nan, and the trajectory optimization is also right, but the value of the objective function is somewhat wrong, and I am checking it carefully
Were you able to solve the problem?
I am getting the same error while writing the below Scaled Lasso in cvx.
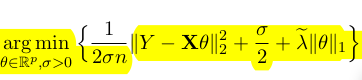
Here theta and sigma are variables.
How can I write this in cvx?
quad_over_lin can be used to handle the first term, which involves quadratic (in theta) divided by linear (in sigma).
help quad_over_lin
quad_over_lin Sum of squares over linear.
Z=quad_over_lin(X,Y), where X is a vector and Y is a scalar, is equal to
SUM(ABS(X).^2)./Y if Y is positive, and +Inf otherwise. Y must be real.If X is a matrix, quad_over_lin(X,Y) is a row vector containing the values of quad_over_lin applied to each column. If X is an N-D array, the operation is applied to the first non-singleton dimension of X. quad_over_lin(X,Y,DIM) takes the sum along the dimension DIM of X. A special value of DIM == 0 is accepted here, which is automatically replaced with DIM == NDIMS(X) + 1. This has the effect of eliminating the sum; thus quad_over_lin( X, Y, NDIMS(X) + 1 ) = ABS( X ).^2 ./ Y. In all cases, Y must be compatible in the same sense as ./ with the squared sum; that is, Y must be a scalar or the same size as SUM(ABS(X).^2,DIM). Disciplined convex programming information: quad_over_lin is convex, nonmontonic in X, and nonincreasing in Y. Thus when used with CVX expressions, X must be convex (or affine) and Y must be concave (or affine).
On writing the first term using quad_over_lin, cvx part is working, but the reconstruction is extremely poor.
What do you mean by “the reconstruction is extremely poor”?
CVX can’t be blamed if the statistical technique implied by the optimization model provided to CVX does not do a good job on your data set. And the choice of lambda may matter a lot.
cvx_begin
variables theta(p, 1) sigcap(1,1);
minimize( (1/(2 * n)) * quad_over_lin(Y - X * theta, sigcap) + sigcap/2 + lambda_final * norm(theta, 1) );
subject to
sigcap > 0;
cvx_end
I am using this but getting very large values for sigcap, where sigcap is standard deviation of the noise.
Yeah, I am using cross-validation for lambda selection.
Is the cvx part written correctly??
Did you use some type of Cross Validation to choose the best value of lambda? See, for instance, http://cvxr.com/cvx/doc/quickstart.html#an-optimal-trade-off-curve . That would involve running many CVX problem instances (optimization problems) for each data set you are analyzing.
Your CVX program looks correct, for a given value of lambda (which you have called lambda_final). But as part of the Cross Validation, you need to solve this optimization problem for each of many candidate values of lambda before choosing the “final” value. And you need to evaluate over a proper range of lambda (which needs to accommodate smaller values than it would if the n were not in the denominator of the first term).
Hello mark, I used to use mosek to simulate, and the result is no longer NaN, but my objective function value is negative, and the optimized objective function value sometimes becomes smaller! It hasn’t converged yet. What’s the matter
Show us the code you ran, and show us all the CVX and solver output.
cvx output:one to seven:-0.26;-0.14;-0.12;0.09;-0.139;-0.09;-0.12
while(itr_tra<=40)
cvx_begin
cvx_solver mosek
variables q1_tra(N,2) q2_tra(N,2) eta2
variables S1(N,6) S2(N,6) t1(N,6) y1(N,6) t2(N,6) y2(N,6)
variables SS1(N,6) SS2(N,6) tt1(N,6) yy1(N,6) tt2(N,6) yy2(N,6)
expressions R_lb_11(N,1) R_lb_12(N,1) R_lb_13(N,1) R_lb_14(N,1) R_lb_15(N,1) R_lb_16(N,1) R_lb_21(N,1) R_lb_22(N,1) R_lb_23(N,1) R_lb_24(N,1) R_lb_25(N,1) R_lb_26(N,1)
expressions Rr_lb_11(N,1) Rr_lb_12(N,1) Rr_lb_13(N,1) Rr_lb_14(N,1) Rr_lb_15(N,1) Rr_lb_16(N,1) Rr_lb_21(N,1) Rr_lb_22(N,1) Rr_lb_23(N,1) Rr_lb_24(N,1) Rr_lb_25(N,1) Rr_lb_26(N,1)
%com
for tt=1:N
n=tt;
A_11(n)=(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(1,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(1,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(1,:)).^2)+N0);
A_12(n)=(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(2,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(2,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(2,:)).^2)+N0);
A_13(n)=(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(3,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(3,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(3,:)).^2)+N0);
A_14(n)=(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(4,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(4,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(4,:)).^2)+N0);
A_15(n)=(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(5,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(5,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(5,:)).^2)+N0);
A_16(n)=(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(6,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(6,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(6,:)).^2)+N0);
A_21(n)=(p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(1,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(1,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(1,:)).^2)+N0);
A_22(n)=(p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(2,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(2,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(2,:)).^2)+N0);
A_23(n)=(p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(3,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(3,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(3,:)).^2)+N0);
A_24(n)=(p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(4,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(4,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(4,:)).^2)+N0);
A_25(n)=(p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(5,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(5,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(5,:)).^2)+N0);
A_26(n)=(p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(6,:)).^2).^2)./log(2)./(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(6,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(6,:)).^2)+N0);
end
for tt=1:N
n=tt;
B_11(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(1,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(1,:)).^2)+N0)./log(2);
B_12(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(2,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(2,:)).^2)+N0)./log(2);
B_13(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(3,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(3,:)).^2)+N0)./log(2);
B_14(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(4,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(4,:)).^2)+N0)./log(2);
B_15(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(5,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(5,:)).^2)+N0)./log(2);
B_16(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(6,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(6,:)).^2)+N0)./log(2);
B_21(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(1,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(1,:)).^2)+N0)./log(2);
B_22(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(2,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(2,:)).^2)+N0)./log(2);
B_23(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(3,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(3,:)).^2)+N0)./log(2);
B_24(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(4,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(4,:)).^2)+N0)./log(2);
B_25(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(5,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(5,:)).^2)+N0)./log(2);
B_26(n)=log(p1(n).*rou_1./(H.^2+norm(q1(n,:)-q(6,:)).^2)+p2(n).*rou_1./(H.^2+norm(q2(n,:)-q(6,:)).^2)+N0)./log(2);
end
for tt=1:N
n=tt;
R_lb_11(n)=-A_11(n).*((q1_tra(n,1)-q(1,1)).^2+(q1_tra(n,2)-q(1,2)).^2-norm(q1(n,:)-q(1,:)).^2)-A_21(n).*((q2_tra(n,1)-q(1,1)).^2+(q2_tra(n,2)-q(1,2)).^2-norm(q2(n,:)-q(1,:)).^2)+B_11(n);
R_lb_12(n)=-A_12(n).*((q1_tra(n,1)-q(2,1)).^2+(q1_tra(n,2)-q(2,2)).^2-norm(q1(n,:)-q(2,:)).^2)-A_22(n).*((q2_tra(n,1)-q(2,1)).^2+(q2_tra(n,2)-q(2,2)).^2-norm(q2(n,:)-q(2,:)).^2)+B_12(n);
R_lb_13(n)=-A_13(n).*((q1_tra(n,1)-q(3,1)).^2+(q1_tra(n,2)-q(3,2)).^2-norm(q1(n,:)-q(3,:)).^2)-A_23(n).*((q2_tra(n,1)-q(3,1)).^2+(q2_tra(n,2)-q(3,2)).^2-norm(q2(n,:)-q(3,:)).^2)+B_13(n);
R_lb_14(n)=-A_14(n).*((q1_tra(n,1)-q(4,1)).^2+(q1_tra(n,2)-q(4,2)).^2-norm(q1(n,:)-q(4,:)).^2)-A_24(n).*((q2_tra(n,1)-q(4,1)).^2+(q2_tra(n,2)-q(4,2)).^2-norm(q2(n,:)-q(4,:)).^2)+B_14(n);
R_lb_15(n)=-A_15(n).*((q1_tra(n,1)-q(5,1)).^2+(q1_tra(n,2)-q(5,2)).^2-norm(q1(n,:)-q(5,:)).^2)-A_25(n).*((q2_tra(n,1)-q(5,1)).^2+(q2_tra(n,2)-q(5,2)).^2-norm(q2(n,:)-q(5,:)).^2)+B_15(n);
R_lb_16(n)=-A_16(n).*((q1_tra(n,1)-q(6,1)).^2+(q1_tra(n,2)-q(6,2)).^2-norm(q1(n,:)-q(6,:)).^2)-A_26(n).*((q2_tra(n,1)-q(6,1)).^2+(q2_tra(n,2)-q(6,2)).^2-norm(q2(n,:)-q(6,:)).^2)+B_16(n);
R_lb_21(n)=-A_11(n).*((q1_tra(n,1)-q(1,1)).^2+(q1_tra(n,2)-q(1,2)).^2-norm(q1(n,:)-q(1,:)).^2)-A_21(n).*((q2_tra(n,1)-q(1,1)).^2+(q2_tra(n,2)-q(1,2)).^2-norm(q2(n,:)-q(1,:)).^2)+B_11(n);
R_lb_22(n)=-A_12(n).*((q1_tra(n,1)-q(2,1)).^2+(q1_tra(n,2)-q(2,2)).^2-norm(q1(n,:)-q(2,:)).^2)-A_22(n).*((q2_tra(n,1)-q(2,1)).^2+(q2_tra(n,2)-q(2,2)).^2-norm(q2(n,:)-q(2,:)).^2)+B_12(n);
R_lb_23(n)=-A_13(n).*((q1_tra(n,1)-q(3,1)).^2+(q1_tra(n,2)-q(3,2)).^2-norm(q1(n,:)-q(3,:)).^2)-A_23(n).*((q2_tra(n,1)-q(3,1)).^2+(q2_tra(n,2)-q(3,2)).^2-norm(q2(n,:)-q(3,:)).^2)+B_13(n);
R_lb_24(n)=-A_14(n).*((q1_tra(n,1)-q(4,1)).^2+(q1_tra(n,2)-q(4,2)).^2-norm(q1(n,:)-q(4,:)).^2)-A_24(n).*((q2_tra(n,1)-q(4,1)).^2+(q2_tra(n,2)-q(4,2)).^2-norm(q2(n,:)-q(4,:)).^2)+B_14(n);
R_lb_25(n)=-A_15(n).*((q1_tra(n,1)-q(5,1)).^2+(q1_tra(n,2)-q(5,2)).^2-norm(q1(n,:)-q(5,:)).^2)-A_25(n).*((q2_tra(n,1)-q(5,1)).^2+(q2_tra(n,2)-q(5,2)).^2-norm(q2(n,:)-q(5,:)).^2)+B_15(n);
R_lb_26(n)=-A_16(n).*((q1_tra(n,1)-q(6,1)).^2+(q1_tra(n,2)-q(6,2)).^2-norm(q1(n,:)-q(6,:)).^2)-A_26(n).*((q2_tra(n,1)-q(6,1)).^2+(q2_tra(n,2)-q(6,2)).^2-norm(q2(n,:)-q(6,:)).^2)+B_16(n);
end
maximize(eta2);
subject to
eta2<=1./N.*(sum(ap*a1(:,1).*(R_lb_11-t2(:,1)./log(2)))+sum(ap*a2(:,1).*(R_lb_21-t1(:,1)./log(2))));
eta2<=1./N.*(sum(ap*a1(:,2).*(R_lb_12-t2(:,2)./log(2)))+sum(ap*a2(:,2).*(R_lb_22-t1(:,2)./log(2))));
eta2<=1./N.*(sum(ap*a1(:,3).*(R_lb_13-t2(:,3)./log(2)))+sum(ap*a2(:,3).*(R_lb_23-t1(:,3)./log(2))));
eta2<=1./N.*(sum(ap*a1(:,4).*(R_lb_14-t2(:,4)./log(2)))+sum(ap*a2(:,4).*(R_lb_24-t1(:,4)./log(2))));
eta2<=1./N.*(sum(ap*a1(:,5).*(R_lb_15-t2(:,5)./log(2)))+sum(ap*a2(:,5).*(R_lb_25-t1(:,5)./log(2))));
eta2<=1./N.*(sum(ap*a1(:,6).*(R_lb_16-t2(:,6)./log(2)))+sum(ap*a2(:,6).*(R_lb_26-t1(:,6)./log(2))));
for tt=1:N
n=tt;
S1(n,1)<=norm(q1(n,:)-q(1,:)).^2+(q1(n,:)-q(1,:))*(q1_tra(n,:)-q1(n,:))'*2;
S1(n,2)<=norm(q1(n,:)-q(2,:)).^2+(q1(n,:)-q(2,:))*(q1_tra(n,:)-q1(n,:))'*2;
S1(n,3)<=norm(q1(n,:)-q(3,:)).^2+(q1(n,:)-q(3,:))*(q1_tra(n,:)-q1(n,:))'*2;
S1(n,4)<=norm(q1(n,:)-q(4,:)).^2+(q1(n,:)-q(4,:))*(q1_tra(n,:)-q1(n,:))'*2;
S1(n,5)<=norm(q1(n,:)-q(5,:)).^2+(q1(n,:)-q(5,:))*(q1_tra(n,:)-q1(n,:))'*2;
S1(n,6)<=norm(q1(n,:)-q(6,:)).^2+(q1(n,:)-q(6,:))*(q1_tra(n,:)-q1(n,:))'*2;
S2(n,1)<=norm(q2(n,:)-q(1,:)).^2+(q2(n,:)-q(1,:))*(q2_tra(n,:)-q2(n,:))'*2;
S2(n,2)<=norm(q2(n,:)-q(2,:)).^2+(q2(n,:)-q(2,:))*(q2_tra(n,:)-q2(n,:))'*2;
S2(n,3)<=norm(q2(n,:)-q(3,:)).^2+(q2(n,:)-q(3,:))*(q2_tra(n,:)-q2(n,:))'*2;
S2(n,4)<=norm(q2(n,:)-q(4,:)).^2+(q2(n,:)-q(4,:))*(q2_tra(n,:)-q2(n,:))'*2;
S2(n,5)<=norm(q2(n,:)-q(5,:)).^2+(q2(n,:)-q(5,:))*(q2_tra(n,:)-q2(n,:))'*2;
S2(n,6)<=norm(q2(n,:)-q(6,:)).^2+(q2(n,:)-q(6,:))*(q2_tra(n,:)-q2(n,:))'*2;
end
for k=1:K
(H.^2+S2(:,k))./(p2.*rou_0)>=exp(-y2(:,k));
(H.^2+S1(:,k))./(p1.*rou_0)>=exp(-y1(:,k));
end
t1>=log(N0+exp(y1));
t2>=log(N0+exp(y2));
for tt=1:N-1
n=tt;
(q1_tra(n+1,1)-q1_tra(n,1)).^2+(q1_tra(n+1,2)-q1_tra(n,2)).^2<=(Vmax*Delta).^2;
(q2_tra(n+1,1)-q2_tra(n,1)).^2+(q2_tra(n+1,2)-q2_tra(n,2)).^2<=(Vmax*Delta).^2;
end
for tt=1:N
n=tt;
2*((q1(n,1)-q2(n,1)).*(q1_tra(n,1)-q2_tra(n,1))+(q1(n,2)-q2(n,2)).*(q1_tra(n,2)-q2_tra(n,2)))-((q1(n,1)-q2(n,1)).^2-(q1(n,2)-q2(n,2)).^2)>=dmin.^2;
end
q1_tra(1,:)==q1_tra(N,:);
q2_tra(1,:)==q2_tra(N,:);
cvx_end;
q1=q1_tra;
q2=q2_tra;
itr_tra=itr_tra+1;
endCalling Mosek 9.1.9: 42636 variables, 15197 equality constraints
For improved efficiency, Mosek is solving the dual problem.
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
MOSEK warning 710: #2 (nearly) zero elements are specified in sparse col ‘’ (5) of matrix ‘A’.
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 15197
Cones : 13756
Scalar variables : 42636
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 158
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.01
Lin. dep. - number : 0
Presolve terminated. Time: 0.05
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 15197
Cones : 13756
Scalar variables : 42636
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 4
Optimizer - solved problem : the primal
Optimizer - Constraints : 7987
Optimizer - Cones : 13756
Optimizer - Scalar variables : 42467 conic : 41268
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.03 dense det. time : 0.00
Factor - ML order time : 0.02 GP order time : 0.00
Factor - nonzeros before factor : 8.06e+04 after factor : 1.38e+05
Factor - dense dim. : 0 flops : 1.77e+07
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.6e+00 6.4e+06 1.6e+05 0.00e+00 1.622567388e+05 0.000000000e+00 1.0e+00 0.13
1 8.3e-01 3.3e+06 1.2e+05 -1.00e+00 1.625449940e+05 -6.844007302e-01 5.2e-01 0.23
2 2.5e-01 9.9e+05 6.4e+04 -1.00e+00 1.625250621e+05 -3.951000283e+00 1.5e-01 0.27
3 3.5e-02 1.4e+05 2.4e+04 -1.00e+00 1.624469083e+05 -3.164850002e+01 2.2e-02 0.30
4 5.3e-03 2.1e+04 9.3e+03 -1.00e+00 1.619355794e+05 -2.064584830e+02 3.3e-03 0.31
5 9.0e-04 3.6e+03 3.8e+03 -9.99e-01 1.589253187e+05 -1.212381975e+03 5.6e-04 0.34
6 1.5e-04 6.0e+02 1.5e+03 -9.91e-01 1.405287018e+05 -7.058878707e+03 9.3e-05 0.38
7 3.5e-05 1.4e+02 6.8e+02 -9.32e-01 7.566182913e+04 -2.704866366e+04 2.2e-05 0.41
8 1.1e-05 4.3e+01 2.5e+02 -6.03e-01 -1.718929909e+04 -5.466771999e+04 6.8e-06 0.44
9 3.1e-06 1.2e+01 3.1e+01 3.36e-01 -4.273799834e+04 -6.110771507e+04 1.9e-06 0.45
10 3.5e-07 1.4e+00 8.9e-01 9.33e-01 -5.473197426e+04 -5.723580010e+04 2.2e-07 0.48
11 2.5e-09 9.8e-03 4.5e-04 1.10e+00 -4.815632208e+04 -4.817367361e+04 1.5e-09 0.52
12 6.0e-10 2.4e-03 5.7e-05 1.06e+00 -1.031350122e+04 -1.031752360e+04 3.8e-10 0.55
13 1.7e-10 6.6e-04 8.7e-06 1.01e+00 -2.687027111e+03 -2.688093465e+03 1.0e-10 0.56
14 3.3e-11 1.3e-04 8.0e-07 1.00e+00 -4.758651526e+02 -4.760709859e+02 2.0e-11 0.59
15 4.5e-12 1.8e-05 4.1e-08 9.99e-01 -7.005231448e+01 -7.008050676e+01 2.8e-12 0.63
16 9.1e-13 3.6e-06 3.9e-09 1.00e+00 -1.388821498e+01 -1.389386276e+01 5.7e-13 0.66
17 2.2e-13 8.7e-07 4.8e-10 9.91e-01 -4.118287457e+00 -4.119593411e+00 1.4e-13 0.69
18 1.2e-13 4.9e-07 2.2e-10 9.35e-01 -2.938900084e+00 -2.939613745e+00 7.6e-14 0.70
19 1.0e-13 4.0e-07 1.7e-10 8.93e-01 -2.645581225e+00 -2.646166177e+00 6.2e-14 0.73
20 8.5e-14 3.4e-07 1.4e-10 8.64e-01 -2.423227961e+00 -2.423725072e+00 5.3e-14 0.77
21 8.1e-14 3.2e-07 1.3e-10 8.41e-01 -2.366097154e+00 -2.366572980e+00 5.0e-14 0.80
22 5.8e-14 2.3e-07 8.5e-11 8.33e-01 -2.000017158e+00 -2.000360207e+00 3.6e-14 0.81
23 4.2e-14 1.7e-07 5.5e-11 7.88e-01 -1.734433178e+00 -1.734680553e+00 2.6e-14 0.84
24 3.3e-14 1.3e-07 3.8e-11 7.55e-01 -1.566123346e+00 -1.566311643e+00 1.9e-14 0.88
25 2.6e-14 2.6e-07 2.1e-11 7.32e-01 -1.354616789e+00 -1.354733816e+00 1.2e-14 0.89
26 2.1e-14 1.9e-07 1.3e-11 7.00e-01 -1.237010398e+00 -1.237090448e+00 8.1e-15 0.92
27 1.4e-14 2.2e-07 4.7e-12 6.65e-01 -1.053808258e+00 -1.053839307e+00 3.6e-15 0.95
28 9.5e-15 7.1e-07 2.1e-12 5.65e-01 -9.345874397e-01 -9.345983435e-01 1.8e-15 0.98
29 6.1e-15 1.2e-06 9.9e-13 4.76e-01 -8.350328864e-01 -8.350337548e-01 9.5e-16 1.00
30 3.9e-15 6.6e-07 5.2e-13 4.03e-01 -7.448690858e-01 -7.448642806e-01 5.2e-16 1.03
31 2.1e-15 4.5e-07 2.3e-13 3.60e-01 -6.349433861e-01 -6.349342863e-01 2.4e-16 1.06
32 1.0e-15 2.3e-06 9.6e-14 2.95e-01 -5.093669674e-01 -5.093547420e-01 1.1e-16 1.09
33 1.3e-15 2.3e-06 8.7e-14 3.19e-01 -4.988999245e-01 -4.988878792e-01 9.7e-17 1.11
34 6.0e-15 4.1e-06 6.4e-14 3.20e-01 -4.691955369e-01 -4.691841885e-01 7.5e-17 1.14
35 5.6e-15 3.9e-06 5.8e-14 3.67e-01 -4.659679978e-01 -4.659574079e-01 7.0e-17 1.17
36 5.3e-15 6.2e-06 4.3e-14 3.91e-01 -4.405490218e-01 -4.405393320e-01 5.5e-17 1.20
37 5.9e-15 3.4e-06 2.9e-14 3.67e-01 -4.052260844e-01 -4.052174075e-01 3.9e-17 1.22
38 5.8e-15 3.1e-06 2.6e-14 3.78e-01 -4.038492389e-01 -4.038412607e-01 3.7e-17 1.25
39 5.9e-15 5.1e-06 1.9e-14 3.83e-01 -3.781973926e-01 -3.781902218e-01 2.9e-17 1.28
40 5.8e-15 8.1e-06 1.4e-14 4.07e-01 -3.563693929e-01 -3.563627043e-01 2.3e-17 1.31
41 5.2e-15 1.1e-05 1.1e-14 4.09e-01 -3.368184658e-01 -3.368123045e-01 1.9e-17 1.34
42 4.8e-15 1.4e-05 8.6e-15 4.13e-01 -3.182400000e-01 -3.182342730e-01 1.6e-17 1.36
43 4.4e-15 1.8e-05 6.6e-15 3.50e-01 -3.004918089e-01 -3.004865494e-01 1.3e-17 1.39
44 3.6e-15 2.3e-05 4.6e-15 4.03e-01 -2.757493016e-01 -2.757445523e-01 9.8e-18 1.42
45 3.5e-15 2.1e-05 4.4e-15 4.78e-01 -2.751525512e-01 -2.751479369e-01 9.6e-18 1.44
46 3.0e-15 5.5e-06 3.4e-15 4.84e-01 -2.623611061e-01 -2.623569892e-01 8.0e-18 1.47
47 2.8e-15 6.6e-06 2.4e-15 4.89e-01 -2.407538801e-01 -2.407502576e-01 6.1e-18 1.50
48 2.4e-15 8.0e-06 2.1e-15 3.96e-01 -2.320222590e-01 -2.320188086e-01 5.5e-18 1.53
49 2.2e-15 5.3e-06 1.8e-15 5.12e-01 -2.280950233e-01 -2.280917587e-01 5.1e-18 1.55
50 2.0e-15 1.4e-05 1.5e-15 5.59e-01 -2.188427646e-01 -2.188397864e-01 4.5e-18 1.58
51 2.2e-15 1.5e-05 9.6e-16 5.39e-01 -1.961789578e-01 -1.961763929e-01 3.2e-18 1.61
52 2.1e-15 1.4e-05 9.2e-16 4.78e-01 -1.950086294e-01 -1.950061141e-01 3.1e-18 1.64
53 2.0e-15 1.3e-05 8.4e-16 5.73e-01 -1.945742211e-01 -1.945718676e-01 3.0e-18 1.67
54 1.7e-15 1.1e-05 6.8e-16 5.99e-01 -1.879121494e-01 -1.879100348e-01 2.6e-18 1.69
55 1.4e-15 9.3e-06 5.6e-16 4.60e-01 -1.792059489e-01 -1.792039425e-01 2.3e-18 1.76
56 1.2e-15 7.2e-06 4.1e-16 4.80e-01 -1.643185911e-01 -1.643167743e-01 1.9e-18 1.84
57 1.1e-15 6.6e-06 3.6e-16 4.79e-01 -1.597719328e-01 -1.597701858e-01 1.8e-18 1.94
58 1.0e-15 6.0e-06 3.2e-16 5.32e-01 -1.555138381e-01 -1.555121597e-01 1.6e-18 2.00
59 8.6e-16 5.0e-06 2.5e-16 4.89e-01 -1.459886058e-01 -1.459870202e-01 1.4e-18 2.09
60 8.3e-16 8.3e-06 2.3e-16 8.02e-01 -1.428796330e-01 -1.428781103e-01 1.3e-18 2.13
61 7.9e-16 7.8e-06 2.1e-16 6.10e-01 -1.406597158e-01 -1.406582255e-01 1.3e-18 2.20
62 7.2e-16 5.9e-06 1.5e-16 6.17e-01 -1.298667691e-01 -1.298654722e-01 9.8e-19 2.27
63 7.2e-16 6.2e-06 1.5e-16 8.06e-01 -1.298623149e-01 -1.298610213e-01 9.8e-19 2.34
64 7.2e-16 6.3e-06 1.4e-16 8.10e-01 -1.298419236e-01 -1.298406310e-01 9.8e-19 2.44
65 7.2e-16 6.4e-06 1.4e-16 8.10e-01 -1.298298803e-01 -1.298285884e-01 9.8e-19 2.52
66 7.2e-16 6.4e-06 1.4e-16 8.06e-01 -1.298298803e-01 -1.298285884e-01 9.8e-19 2.61
67 7.2e-16 6.4e-06 1.4e-16 9.95e-01 -1.298298803e-01 -1.298285884e-01 9.8e-19 2.72
Optimizer terminated. Time: 2.89
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -1.2982988034e-01 nrm: 1e+00 Viol. con: 2e-08 var: 3e-11 cones: 5e-13
Dual. obj: -1.2982858842e-01 nrm: 7e+07 Viol. con: 0e+00 var: 1e+01 cones: 0e+00
Optimizer summary
Optimizer - time: 2.89
Interior-point - iterations : 68 time: 2.84
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Solved
Optimal value (cvx_optval): -0.129829
This is the seventh solver output
is there some reason why the optimal objective value (eta2 being maximized) can’t be negative? Mosek does issue a warning about near zero input data, but claims to have solved the problem to optimality. If you think there should be a nonnegative `eta2 for this 7th problem, can you produce it and show that it satisfies all constraints?
As for whether your iterative scheme converges, do you have any proof that it should converge to anything? Not every iterative scheme does. Not only might it not converge, but the optimal objective values could get worse - perhaps that happened to you? You might get a wilder and wilder sequence of problems which don’t converge to anything, or endlessly oscillate.
Hello Mark, I am currently simulating a mathematical model in a SCI paper. The objective function in the paper is convergent, because this problem is an approximation of a non negative function, and negative values cannot occur.
Is it convergence when I’m in shock?
The objective function in the paper is convergent, because this problem is an approximation of a non negative function, and negative values cannot occur.
That argument fails to convince me. Maybe the paper has more details, but I have not seen them, and that is getting out of scope of this forum.
Even if the paper has an example which converges, the tiniest change in input data, starting value, or solver used (or transformations by CVX, etc.) could make the difference between convergence and non-convergemce.