how to solve"Illegal addition encountered (e.g., {convex} + {concave})."
You have obviously violated CVX’s rules. But you have to show us more for us to be able to say more.
It might be something like
x’Qx - 0.1*x’Qx <= 1
that is the problem assuming Q is PSD. If you write
0.9 x’Qx <= 0.5
it works.
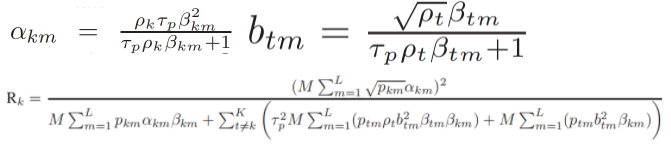
The details of my question are as follow.I want to obtain the maximal value of Rk,the variable is pk.But the concavity and convexity of the three parts of the denominator are different, so the addition will report an error"Illegal addition encountered (e.g., {convex} + {concave})."How can I solve this problem?Thanks for your answer.
The first step is for you to prove that R_k is concave. That looks dubious enough that I will mark this problem as non-convex until you have shown otherwise.
Thank you for your suggestion.
I limited the scope of the optimization variable in ‘subject to’,the variable should be between 0 and 6000, but the optimized result far exceeds this value. Why is this?
In order for us to diagnose, you need to show us your program and the solver and CVX output Did CVX report that the optimal solution was found?
cvx_begin gp
cvx_quiet(true); %This suppresses screen output from the solver
variable nu(L,K); %Power allocation
expression SINR(K,1);
maximize prod(SINR)
subject to
for k=1:K
NNLL(prod(sqrt(nu(:,k)))prod(a(:,k)))^(2/L)/((Nsum(nu(:,k).a(:,k).beta(:,k)))+(tau_ptau_pNpsum(sum(nu(:,[1:k-1 k+1:end]).b(:,[1:k-1 k+1:end]).^2.beta(:,[1:k-1 k+1:end]).repmat(beta(:,k),[1 K-1]))))+(Nsum(sum(nu(:,[1:k-1 k+1:end]).b(:,[1:k-1 k+1:end]).^2.repmat(beta(:,k),[1 K-1]))))+1)>= SINRconstraint;
SINR(k)=NNLL(prod(sqrt(nu(:,k)))prod(a(:,k)))^(2/L)/((Nsum(nu(:,k).a(:,k).beta(:,k)))+(tau_ptau_pNpsum(sum(nu(:,[1:k-1 k+1:end]).*b(:,[1:k-1 k+1:end]).^2.*beta(:,[1:k-1 k+1:end]).repmat(beta(:,k),[1 K-1]))))+(Nsum(sum(nu(:,[1:k-1 k+1:end]).*b(:,[1:k-1 k+1:end]).^2.*repmat(beta(:,k),[1 K-1]))))+1);
end
for l = 1:L
nu(l,:)>=0;
sum(nu(l,:)) <= 6000;
end
cvx_end
The above is my code. My optimization variable is nu. I limited its value to 0~6000. The optimization result shows that the optimal solution is not found. nu is all 3*e300. What is going on?
You haven’t shown us the solver and CVX output. Did the solver numerically fail, or did it report the problem as infeasible?
Do not use cvx_quiet(true); until you have the program working satisfactorily.
If you have Mosek available, use it as solver (wirh CVX 2.2). Otherwise follow the directions at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions .
If after doing so the problem is reported as infeasible, follow the advice, except for section 1, at https://yalmip.github.io/debugginginfeasible ,
I use Mosek solver wirh CVX 2.2. And CVX output are as follows.
Calling Mosek 9.1.9: 24800 variables, 8480 equality constraints
For improved efficiency, Mosek is solving the dual problem.
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 8480
Cones : 8240
Scalar variables : 24800
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 8480
Cones : 8240
Scalar variables : 24800
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 16
Optimizer - solved problem : the primal
Optimizer - Constraints : 8440
Optimizer - Cones : 8240
Optimizer - Scalar variables : 24750 conic : 24720
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.20 dense det. time : 0.00
Factor - ML order time : 0.16 GP order time : 0.00
Factor - nonzeros before factor : 8.32e+05 after factor : 2.13e+06
Factor - dense dim. : 0 flops : 6.93e+08
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.6e+02 2.0e+01 9.6e+04 0.00e+00 9.563843292e+04 0.000000000e+00 1.0e+00 0.30
1 6.3e+01 7.8e+00 3.9e+04 -3.94e-01 6.314256251e+04 0.000000000e+00 3.9e-01 0.47
2 1.1e+01 1.3e+00 5.7e+03 9.66e-03 1.940938178e+04 0.000000000e+00 6.7e-02 0.55
3 6.1e+00 7.6e-01 2.8e+03 4.26e-01 1.316309365e+04 0.000000000e+00 3.8e-02 0.64
4 4.2e+00 5.2e-01 1.7e+03 5.36e-01 9.941760024e+03 0.000000000e+00 2.6e-02 0.72
5 2.1e+00 2.6e-01 6.2e+02 6.58e-01 5.521054664e+03 0.000000000e+00 1.3e-02 0.81
6 7.2e-01 9.0e-02 1.3e+02 8.17e-01 2.033912381e+03 0.000000000e+00 4.5e-03 0.89
7 3.1e-01 3.8e-02 3.7e+01 9.25e-01 8.804971097e+02 0.000000000e+00 1.9e-03 0.97
8 1.9e-01 2.3e-02 1.7e+01 1.02e+00 5.281040561e+02 0.000000000e+00 1.2e-03 1.06
9 7.5e-02 9.3e-03 4.0e+00 1.10e+00 1.944122882e+02 0.000000000e+00 4.7e-04 1.14
10 4.1e-02 5.0e-03 1.4e+00 1.27e+00 9.276369905e+01 0.000000000e+00 2.5e-04 1.22
11 9.0e-03 1.1e-03 1.3e-01 1.28e+00 1.737751741e+01 0.000000000e+00 5.5e-05 1.30
12 6.2e-04 7.7e-05 2.2e-03 1.14e+00 1.120571176e+00 0.000000000e+00 3.8e-06 1.38
13 1.9e-07 2.4e-08 1.2e-08 1.01e+00 3.458461348e-04 0.000000000e+00 1.2e-09 1.45
14 2.9e-12 3.6e-13 6.9e-16 1.00e+00 5.277182658e-09 0.000000000e+00 1.8e-14 1.55
Optimizer terminated. Time: 1.61
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 5.2771826584e-09 nrm: 8e-10 Viol. con: 9e-12 var: 0e+00 cones: 0e+00
Dual. obj: 0.0000000000e+00 nrm: 2e+01 Viol. con: 0e+00 var: 1e-12 cones: 0e+00
Optimizer summary
Optimizer - time: 1.61
Interior-point - iterations : 14 time: 1.55
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Solved
Optimal value (cvx_optval): +0
Mosek solves your problem nicely it seems.
@jessie_sun Were you previously not using Mosek? Did something else change between your not getting a solution and Mosek solving your problem?
I commented out this sentence“cvx_begin quiet (true)”
Thank you for your patience to help me answer the question.
cvx_begin gp
cvx_quiet(true);
variable nu(L,K); %Power allocation
expression SINR(K,1);
maximize prod(SINR)
subject to
for k=1:K
NNLL(prod(sqrt(nu(:,k)))prod(a_s14(:,k)))^(2/L)/((Nsum(nu(:,k).a_s14(:,k).beta(:,k)))+(tau_ptau_pNp_s14sum(sum(nu(:,[1:k-1 k+1:end]).b_s14(:,[1:k-1 k+1:end]).^2.beta(:,[1:k-1 k+1:end]).repmat(beta(:,k),[1 K-1]))))+(Nsum(sum(nu(:,[1:k-1 k+1:end]).b_s14(:,[1:k-1 k+1:end]).^2.repmat(beta(:,k),[1 K-1]))))+1)>= SINRconstraint;
SINR(k)=NNLL(prod(sqrt(nu(:,k)))prod(a_s14(:,k)))^(2/L)/((Nsum(nu(:,k).a_s14(:,k).beta(:,k)))+(tau_ptau_pNp_s14sum(sum(nu(:,[1:k-1 k+1:end]).*b_s14(:,[1:k-1 k+1:end]).^2.*beta(:,[1:k-1 k+1:end]).repmat(beta(:,k),[1 K-1]))))+(Nsum(sum(nu(:,[1:k-1 k+1:end]).*b_s14(:,[1:k-1 k+1:end]).^2.*repmat(beta(:,k),[1 K-1]))))+1);
end
for l = 1:L
nu(l,:)>=0;
sum(nu(l,:)) <= Pmax;
end
cvx_end
The above is my optimization program, which can solve the problem but cannot make my objective function optimal, and even the objective function value is not as good as setting variable nu to all equal values,why?
Expressions are initialized in CVX to (array of) zero. So that is the value of all elements of SINR at the time the objective function is defined. So in effect you were only specifying a feasibility problem, for which any feasible solution is “optimal”.
You need to more the for loop in which SINR is set, to before the objective function in which SINR is used.
In order to see what the true optimal values of SINR are, you will need to compute it after CVX ends starting from the optimal variable values. The value expressions have after CVX concludes is not guaranteed to be optimal, even though the optimal variable values were found and the problem correctly solved. That is just a quirk of CVX.
The problem has been solved, thank you very much for your answers.
Now I want to optimize two variables nu and rou at the same time,but code in bold reports an error‘’Illegal addition encountered (e.g., {convex} + {concave}).‘’
What should I do to solve this error?Below is part of my code:
cvx_begin gp
cvx_quiet(true); %This suppresses screen output from the solver
variables nu(L,K) rou(1,K);
subject to
for k=1:K
**NNLL(prod(sqrt(nu(:,k)))*prod(rou(k)*tau_p.*beta(:,k).*beta(:,k)./(rou(k)*tau_p.beta(:,k)+1)))^(2/L)/((Nsum(nu(:,k).*rou(k)*tau_p.*beta(:,k).beta(:,k)./(rou(k)tau_p.beta(:,k)+1).beta(:,k)))+(tau_ptau_pNsum(sum(nu(:,[1:k-1 k+1:end]).((rou([1:k-1 k+1:end])).^(3/2).beta(:,[1:k-1 k+1:end])./(tau_prou([1:k-1 k+1:end]).*beta(:,[1:k-1 k+1:end])+1)).^2.beta(:,[1:k-1 k+1:end]).repmat(beta(:,k),[1 K-1]))))+(Nsum(sum(nu(:,[1:k-1 k+1:end]).(sqrt(rou([1:k-1 k+1:end])).beta(:,[1:k-1 k+1:end])./(tau_prou([1:k-1 k+1:end]).beta(:,[1:k-1 k+1:end])+1)).^2.repmat(beta(:,k),[1 K-1]))))+1)>= SINRconstraint;
rou(1,k)>=0.0001;
rou(1,k)<=rouMax;
end
Have you proven your model is (transformable to) convex? If you are using gp mode, you must follow the appropriate rules. http://cvxr.com/cvx/doc/gp.html
cvx_begin gp
variable nu(L,K); %Power allocation
maximize prod([NNLL(prod(sqrt(nu(:,1)))prod(a(:,1)))^(2/L)/((Nsum(nu(:,1).a(:,1).beta(:,1)))+(tau_ptau_pNpsum(sum(nu(:,[1:1-1 1+1:end]).b(:,[1:1-1 1+1:end]).^2.beta(:,[1:1-1 1+1:end]).repmat(beta(:,1),[1 K-1]))))+(Nsum(sum(nu(:,[1:1-1 1+1:end]).b(:,[1:1-1 1+1:end]).^2.repmat(beta(:,1),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,2)))prod(a(:,2)))^(2/L)/((Nsum(nu(:,2).a(:,2).beta(:,2)))+(tau_ptau_pNpsum(sum(nu(:,[1:2-1 2+1:end]).b(:,[1:2-1 2+1:end]).^2.beta(:,[1:2-1 2+1:end]).repmat(beta(:,2),[1 K-1]))))+(Nsum(sum(nu(:,[1:2-1 2+1:end]).b(:,[1:2-1 2+1:end]).^2.repmat(beta(:,2),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,3)))prod(a(:,3)))^(2/L)/((Nsum(nu(:,3).a(:,3).beta(:,3)))+(tau_ptau_pNpsum(sum(nu(:,[1:3-1 3+1:end]).b(:,[1:3-1 3+1:end]).^2.beta(:,[1:3-1 3+1:end]).repmat(beta(:,3),[1 K-1]))))+(Nsum(sum(nu(:,[1:3-1 3+1:end]).b(:,[1:3-1 3+1:end]).^2.repmat(beta(:,3),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,4)))prod(a(:,4)))^(2/L)/((Nsum(nu(:,4).a(:,4).beta(:,4)))+(tau_ptau_pNpsum(sum(nu(:,[1:4-1 4+1:end]).b(:,[1:4-1 4+1:end]).^2.beta(:,[1:4-1 4+1:end]).repmat(beta(:,4),[1 K-1]))))+(Nsum(sum(nu(:,[1:4-1 4+1:end]).b(:,[1:4-1 4+1:end]).^2.repmat(beta(:,4),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,5)))prod(a(:,5)))^(2/L)/((Nsum(nu(:,5).a(:,5).beta(:,5)))+(tau_ptau_pNpsum(sum(nu(:,[1:5-1 5+1:end]).b(:,[1:5-1 5+1:end]).^2.beta(:,[1:5-1 5+1:end]).repmat(beta(:,5),[1 K-1]))))+(Nsum(sum(nu(:,[1:5-1 5+1:end]).b(:,[1:5-1 5+1:end]).^2.repmat(beta(:,5),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,6)))prod(a(:,6)))^(2/L)/((Nsum(nu(:,6).a(:,6).beta(:,6)))+(tau_ptau_pNpsum(sum(nu(:,[1:6-1 6+1:end]).b(:,[1:6-1 6+1:end]).^2.beta(:,[1:6-1 6+1:end]).repmat(beta(:,6),[1 K-1]))))+(Nsum(sum(nu(:,[1:6-1 6+1:end]).b(:,[1:6-1 6+1:end]).^2.repmat(beta(:,6),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,7)))prod(a(:,7)))^(2/L)/((Nsum(nu(:,7).a(:,7).beta(:,7)))+(tau_ptau_pNpsum(sum(nu(:,[1:7-1 7+1:end]).b(:,[1:7-1 7+1:end]).^2.beta(:,[1:7-1 7+1:end]).repmat(beta(:,7),[1 K-1]))))+(Nsum(sum(nu(:,[1:7-1 7+1:end]).b(:,[1:7-1 7+1:end]).^2.repmat(beta(:,7),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,8)))prod(a(:,8)))^(2/L)/((Nsum(nu(:,8).a(:,8).beta(:,8)))+(tau_ptau_pNpsum(sum(nu(:,[1:8-1 8+1:end]).b(:,[1:8-1 8+1:end]).^2.beta(:,[1:8-1 8+1:end]).repmat(beta(:,8),[1 K-1]))))+(Nsum(sum(nu(:,[1:8-1 8+1:end]).b(:,[1:8-1 8+1:end]).^2.repmat(beta(:,8),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,9)))prod(a(:,9)))^(2/L)/((Nsum(nu(:,9).a(:,9).beta(:,9)))+(tau_ptau_pNpsum(sum(nu(:,[1:9-1 9+1:end]).b(:,[1:9-1 9+1:end]).^2.beta(:,[1:9-1 9+1:end]).repmat(beta(:,9),[1 K-1]))))+(Nsum(sum(nu(:,[1:9-1 9+1:end]).b(:,[1:9-1 9+1:end]).^2.repmat(beta(:,9),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,10)))prod(a(:,10)))^(2/L)/((Nsum(nu(:,10).a(:,10).beta(:,10)))+(tau_ptau_pNpsum(sum(nu(:,[1:10-1 10+1:end]).b(:,[1:10-1 10+1:end]).^2.beta(:,[1:10-1 10+1:end]).repmat(beta(:,10),[1 K-1]))))+(Nsum(sum(nu(:,[1:10-1 10+1:end]).b(:,[1:10-1 10+1:end]).^2.repmat(beta(:,10),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,11)))prod(a(:,11)))^(2/L)/((Nsum(nu(:,11).a(:,11).beta(:,11)))+(tau_ptau_pNpsum(sum(nu(:,[1:11-1 11+1:end]).b(:,[1:11-1 11+1:end]).^2.beta(:,[1:11-1 11+1:end]).repmat(beta(:,11),[1 K-1]))))+(Nsum(sum(nu(:,[1:11-1 11+1:end]).b(:,[1:11-1 11+1:end]).^2.repmat(beta(:,11),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,12)))prod(a(:,12)))^(2/L)/((Nsum(nu(:,12).a(:,12).beta(:,12)))+(tau_ptau_pNpsum(sum(nu(:,[1:12-1 12+1:end]).b(:,[1:12-1 12+1:end]).^2.beta(:,[1:12-1 12+1:end]).repmat(beta(:,12),[1 K-1]))))+(Nsum(sum(nu(:,[1:12-1 12+1:end]).b(:,[1:12-1 12+1:end]).^2.repmat(beta(:,12),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,13)))prod(a(:,13)))^(2/L)/((Nsum(nu(:,13).a(:,13).beta(:,13)))+(tau_ptau_pNpsum(sum(nu(:,[1:13-1 13+1:end]).b(:,[1:13-1 13+1:end]).^2.beta(:,[1:13-1 13+1:end]).repmat(beta(:,13),[1 K-1]))))+(Nsum(sum(nu(:,[1:13-1 13+1:end]).b(:,[1:13-1 13+1:end]).^2.repmat(beta(:,13),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,14)))prod(a(:,14)))^(2/L)/((Nsum(nu(:,14).a(:,14).beta(:,14)))+(tau_ptau_pNpsum(sum(nu(:,[1:14-1 14+1:end]).b(:,[1:14-1 14+1:end]).^2.beta(:,[1:14-1 14+1:end]).repmat(beta(:,14),[1 K-1]))))+(Nsum(sum(nu(:,[1:14-1 14+1:end]).b(:,[1:14-1 14+1:end]).^2.repmat(beta(:,14),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,15)))prod(a(:,15)))^(2/L)/((Nsum(nu(:,15).a(:,15).beta(:,15)))+(tau_ptau_pNpsum(sum(nu(:,[1:15-1 15+1:end]).b(:,[1:15-1 15+1:end]).^2.beta(:,[1:15-1 15+1:end]).repmat(beta(:,15),[1 K-1]))))+(Nsum(sum(nu(:,[1:15-1 15+1:end]).b(:,[1:15-1 15+1:end]).^2.repmat(beta(:,15),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,16)))prod(a(:,16)))^(2/L)/((Nsum(nu(:,16).a(:,16).beta(:,16)))+(tau_ptau_pNpsum(sum(nu(:,[1:16-1 16+1:end]).b(:,[1:16-1 16+1:end]).^2.beta(:,[1:16-1 16+1:end]).repmat(beta(:,16),[1 K-1]))))+(Nsum(sum(nu(:,[1:16-1 16+1:end]).b(:,[1:16-1 16+1:end]).^2.repmat(beta(:,16),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,17)))prod(a(:,17)))^(2/L)/((Nsum(nu(:,17).a(:,17).beta(:,17)))+(tau_ptau_pNpsum(sum(nu(:,[1:17-1 17+1:end]).b(:,[1:17-1 17+1:end]).^2.beta(:,[1:17-1 17+1:end]).repmat(beta(:,17),[1 K-1]))))+(Nsum(sum(nu(:,[1:17-1 17+1:end]).b(:,[1:17-1 17+1:end]).^2.repmat(beta(:,17),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,18)))prod(a(:,18)))^(2/L)/((Nsum(nu(:,18).a(:,18).beta(:,18)))+(tau_ptau_pNpsum(sum(nu(:,[1:18-1 18+1:end]).b(:,[1:18-1 18+1:end]).^2.beta(:,[1:18-1 18+1:end]).repmat(beta(:,18),[1 K-1]))))+(Nsum(sum(nu(:,[1:18-1 18+1:end]).b(:,[1:18-1 18+1:end]).^2.repmat(beta(:,18),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,19)))prod(a(:,19)))^(2/L)/((Nsum(nu(:,19).a(:,19).beta(:,19)))+(tau_ptau_pNpsum(sum(nu(:,[1:19-1 19+1:end]).b(:,[1:19-1 19+1:end]).^2.beta(:,[1:19-1 19+1:end]).repmat(beta(:,19),[1 K-1]))))+(Nsum(sum(nu(:,[1:19-1 19+1:end]).b(:,[1:19-1 19+1:end]).^2.repmat(beta(:,19),[1 K-1]))))+1),NNLL(prod(sqrt(nu(:,20)))prod(a(:,20)))^(2/L)/((Nsum(nu(:,20).a(:,20).beta(:,20)))+(tau_ptau_pNpsum(sum(nu(:,[1:20-1 20+1:end]).b(:,[1:20-1 20+1:end]).^2.beta(:,[1:20-1 20+1:end]).repmat(beta(:,20),[1 K-1]))))+(Nsum(sum(nu(:,[1:20-1 20+1:end]).b(:,[1:20-1 20+1:end]).^2.repmat(beta(:,20),[1 K-1]))))+1)])
subject to
for k=1:K
NNLL(prod(sqrt(nu(:,k)))prod(a(:,k)))^(2/L)/((Nsum(nu(:,k).a(:,k).beta(:,k)))+(tau_ptau_pNpsum(sum(nu(:,[1:k-1 k+1:end]).*b(:,[1:k-1 k+1:end]).^2.*beta(:,[1:k-1 k+1:end]).repmat(beta(:,k),[1 K-1]))))+(Nsum(sum(nu(:,[1:k-1 k+1:end]).*b(:,[1:k-1 k+1:end]).^2.*repmat(beta(:,k),[1 K-1]))))+1)>= 1.16;
end
for l = 1:L
nu(l,:)>=0;
sum(nu(l,:)) <= Pmax;
end
cvx_end
Calling Mosek 9.1.9: 12720 variables, 4440 equality constraints
For improved efficiency, Mosek is solving the dual problem.
MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 4440
Cones : 4220
Scalar variables : 12720
Matrix variables : 0
Integer variables : 0
Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.08
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 4440
Cones : 4220
Scalar variables : 12720
Matrix variables : 0
Integer variables : 0
Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 4420
Optimizer - Cones : 4220
Optimizer - Scalar variables : 12690 conic : 12660
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.11 dense det. time : 0.00
Factor - ML order time : 0.06 GP order time : 0.00
Factor - nonzeros before factor : 4.18e+05 after factor : 1.18e+06
Factor - dense dim. : 0 flops : 4.26e+08
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.6e+02 2.1e+01 5.3e+04 0.00e+00 5.285614923e+04 0.000000000e+00 1.0e+00 0.22
1 6.4e+01 8.5e+00 2.2e+04 -3.87e-01 3.553344168e+04 0.000000000e+00 4.0e-01 0.42
2 2.1e+01 2.8e+00 6.8e+03 -4.02e-02 1.916394042e+04 0.000000000e+00 1.3e-01 0.47
3 1.3e+01 1.7e+00 3.8e+03 2.78e-01 1.409216640e+04 0.000000000e+00 8.1e-02 0.52
4 6.4e+00 8.4e-01 1.5e+03 4.53e-01 8.081844494e+03 0.000000000e+00 4.0e-02 0.56
5 2.3e+00 3.0e-01 3.2e+02 7.36e-01 3.052369861e+03 0.000000000e+00 1.4e-02 0.61
6 5.4e-01 7.0e-02 4.1e+01 8.51e-01 7.837548965e+02 0.000000000e+00 3.3e-03 0.66
7 1.6e-01 2.1e-02 7.9e+00 8.17e-01 2.653000114e+02 0.000000000e+00 9.8e-04 0.70
8 1.1e-01 1.5e-02 5.8e+00 3.77e-01 2.354344768e+02 0.000000000e+00 6.9e-04 0.75
9 4.6e-02 6.0e-03 2.9e+00 8.78e-02 1.919165560e+02 0.000000000e+00 2.8e-04 0.81
10 7.2e-03 9.5e-04 1.1e+00 -5.10e-01 1.955213555e+02 0.000000000e+00 4.5e-05 0.86
11 1.6e-04 2.1e-05 1.5e-01 -9.18e-01 1.771099083e+02 0.000000000e+00 1.0e-06 0.91
12 7.2e-08 9.5e-09 3.2e-03 -9.98e-01 -1.797174308e+04 0.000000000e+00 4.5e-10 0.95
13 4.1e-11 1.4e-13 1.2e-05 -1.00e+00 -1.188591924e+09 0.000000000e+00 6.8e-15 0.98
14 3.0e-11 4.2e-07 2.9e-05 -1.00e+00 -2.383089206e-03 0.000000000e+00 -1.1e-07 1.03
Optimizer terminated. Time: 1.11
Interior-point solution summary
Problem status : DUAL_INFEASIBLE
Solution status : DUAL_INFEASIBLE_CER
Primal. obj: -2.3830892057e-03 nrm: 7e+00 Viol. con: 3e-11 var: 0e+00 cones: 0e+00
Optimizer summary
Optimizer - time: 1.11
Interior-point - iterations : 14 time: 1.03
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
Status: Infeasible
Optimal value (cvx_optval): -Inf
The objective function is the product of the rates of 20 users. I want to maximize it. The variable is the power nu. The limiting condition is that the rate of each user must be greater than the constant 1.16. However, the cvx solution result shows that it is Infeasible, and the returned nu is 1.0e+300. What should I do to solve this problem?