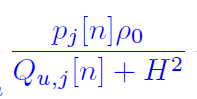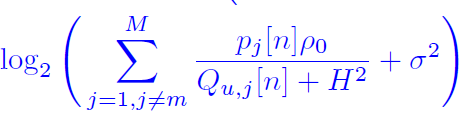How to fix: Cannot perform the operation: {positive constant} ./ {real affine}

1

I want to type below formula (Q is the only term that I want to optimize) :
image
However, cvx give me the error:

Error using .*
Disciplined convex programming error:
Cannot perform the operation: {positive
constant} ./ {real affine}

Error in ./ (line 19)
z = times( x, y, ‘./’ );

Error in * (line 36)
z = feval( oper, x, y );

Error in / (line 15)
z = mtimes( x, y, ‘rdivide’ );

Error in main (line 122)
temp2(u,m,n) = power.p_m(m,n) * db2pow(pl.rho) / ( Q(u,m,n) + pos.H^2 );

How do I fix it?

following is the code:

for u = 1:basic.U
    for m = 1:basic.M
        for n = 1:basic.N
            temp2(u,m,n) = power.p_m(m,n) * db2pow(pl.rho) / ( Q(u,m,n) + pos.H^2 );
        end
    end
end
2

Presuming Q > -H^2, use inv_pos.

3

Yes, it does solve the problem, but after that I put “temp2” in a log term, it has the following problem:

Error using cvx/log
Disciplined convex programming error:
Illegal operation: log( {convex} ).

Error in main (line 136)
Q_log_term(u,m,n) = log( interference + db2pow(power.noise) ) / log(2);

Here’s the code:

for u = 1:basic.U
    for m = 1:basic.M
        for n = 1:basic.N

            vec = ones(basic.M,1);
            vec(m) = 0;

            interference = temp2(u,:,n) * vec;
            Q_log_term(u,m,n) = log( interference + db2pow(power.noise) ) / log(2);

        end
    end
end

and I want to implement this formula:
image

I have read this topic: Problem of disciplined convex programming error: Illegal operation: log( {convex} ),
but I have no idea either how to express as the form x*log(1+y/x) or use log_sum_exp , log_sum_inv.

4