Hello, everyone! How can I express I2 ?
Constraint: I1 - I2-r0>=C0
r0 and C0 are both real value. sk(1,N) is variable.
for i=1:N
a(i)=sum_square(y-w(:,i))
end
I1= -sum(a);
Thank you for your attention very much!
Doesn’t your previous topic Log-sum-inv，is it right address this?
Yes, I have deduced Log-sum-inv. But it is complicated， is there a simpler expression ?
The two formulations I know of are provided in section 5.2.7 Log-sum-inv of https://docs.mosek.com/modeling-cookbook/expo.html#modeling-with-the-exponential-cone
That’s all right, thank you Mark!
@Shuzhen Sorry for bothering. May I know how you express your formula later? I have the same formula but can’t express it. Thanks.
@Ben Have you read How to express log(1+ sum ( 1./x ) ) in CVX? - #2 by Mark_L_Stone and the Mosek Modeling Cookbook section on log-sum-inv to which it refers?
if that doesn’t suffice, please show your mathematical problem formulation, and indicate what you are having trouble with,
I have tried to express it with Log_sum_inv, but I don’t know if it is right as we not do the work latter.
@Shuzhen Can I have a look at your code as a reference, thanks a lot!!!
variable yi(1,K)
variable sk(1,K)
for i=1:8
skk(i)=power(norm(y_f-w(:,i)),2)+2*(y_f-w(:,i))'*(y-y_f)+H_U^2;
end
for i=1:K
if a_f(i)==1
xi(i)=1/roll;
xi(i)>=exp(yi(i));
for i=1:K
ex=ex+exp(yi(i));
end
for k=1:K
if(k~=i)
(H_U^2+sk(i))/(beta_1*pii_f(k))>=exp(-yi(k));
end
end
c>=log(ex);
end
sk(i)<=skk(i);
end
You should use log_sum_exp
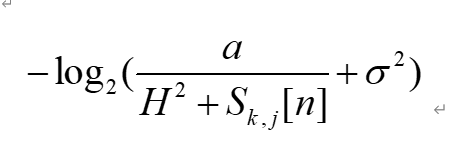
Hello, excuse me, may I use log2( ro*inv_pos(H^2+S(n,k,j)) in cvx, it shows: Illegal operation: log( {convex} ). How should I fix this? Thank you very much
As stated above, Section 5.2.7 log-sum-inv of Mosek Modeling Cookbook . Use log_sum_exp for the 1st constraint of the 1st approach. Divide by log(2) in the appropriate place to account for log2 as opposed to log.
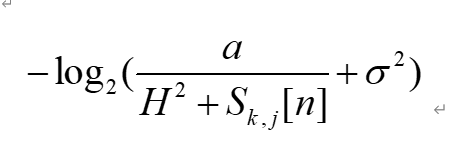
Hello, please let me know. I have expressed it according to: -log2(ro*inv_pos(H^2+S(n,k,j))), where ro and H are constants, but after running the program, Illegal will still appear. operation: log( {convex} ). , what should I do to solve this problem? thanks a lot!!!
Please read my preceding post.
I read it but I don’t understand it very well, and there is a “-” in front of me. Can you give me some guidance? Thank you so much
Log( {convex} ) is almost the same as your problem, except that you would need log(sigma^2) instead of 0 as the first element in the argument of log_sum_exp And you need to divide log_sum_exp by log(2) Then use t in place of log2(...), so -t in place of -log2(...) . The model will only be correct if you use -t in a way in which concave would be allowed.
(RRR(n,k)-log( ro*inv_pos(H^2+S(n,k,j)) )/log(2))
But there is a variable “RRR” in front of my formula, which contains variables. So can I use this method? Thank you so much！！
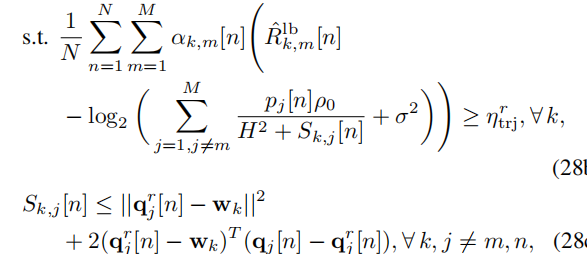
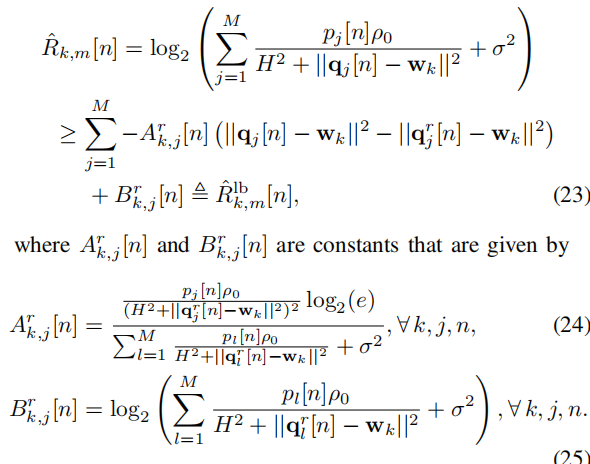
我的原问题在这。
I have no idea what all this notation is or what the optimization variables are. You can add affine (or concave) terms to a concave expression, and still have a concave expression, which can therefore be on the LHS of >= constant.