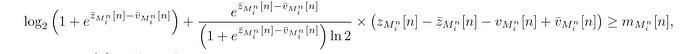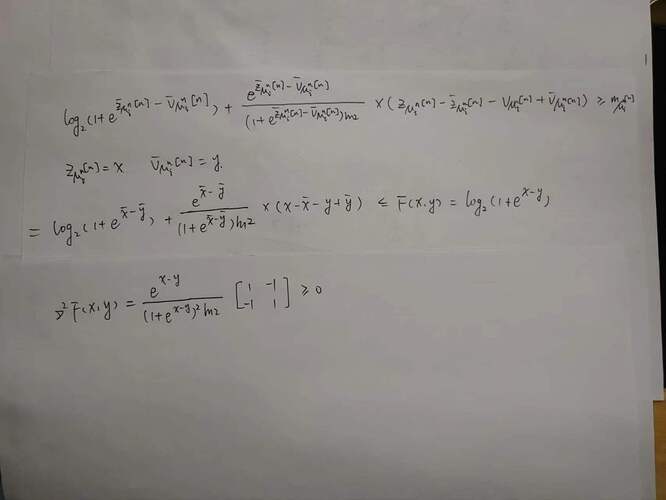Thank you for your reply. I may need to ask for your help again.
I replace Z[n],V[n] on the left side of the constraint with x, y and make a first-order Taylor approximation, which allows me to find that the Hessian matrix is semi-definite.
I apologize for just forgetting to post my error report.
Here’s my complete simulation code.
function [delta_T, P] = cvx_update_P(rou, r, H, Smax, N, num_SNs, citys, Xur, M_star, Pmax, re, Tth)
cvx_begin
variable P(Smax,N)
variable M(Smax,N)
variable Z(Smax,N)
variable Z_B(Smax,N)
variable t(Smax,N)
variable u(Smax,N)
variable V(Smax,N)
variable V_B(Smax,N)
variable delta_T(Smax,N)
variable sums_A(1, 100);
minimize(delta_T)
subject to
%约束2
for i = 1:Smax
for j = 1:N
city_indices = M_star(i, j); % 获取第i个城市的序号
x_coordinates = citys(city_indices, 1); % 获取城市的坐标
y_coordinates = citys(city_indices, 2);
% LHS >= Z(i.j) - Z_B(i,j) + 1
% (rouP(i,j))/(H^2 + (Xur(r,j) - x_coordinates)^2 + y_coordinates^2) >= exp(Z(i,j))(Z(i,j)…
% - Z_B(i,j) + 1);
(rou*P(i,j))/(H^2 + (Xur(r,j) - x_coordinates)^2 + y_coordinates^2) >= Z(i,j) - Z_B(i,j) + 1;
{1,u(i,j),t(i,j)} == rotated_lorentz(1);
{u(i,j),t(i,j),Z(i,j)} == exponential(1);
end
end
%约束3
for i = 1:Smax
for j = 1:N
city_indices = M_star(i, j); % 获取第i个城市的序号
x_coordinates = citys(city_indices, 1); % 获取城市的坐标
y_coordinates = citys(city_indices, 2);
A(i, j) = (rou*P(i,j))/(H^2 + (Xur(r,j) - x_coordinates)^2 + y_coordinates^2);
end
sums_A(:, i) == sum(A(:, i));
{1,u(i,j),t(i,j)} == rotated_lorentz(1);
{u(i,j),t(i,j),V(i,j)} == exponential(1);
sums_A(:, i) + 1 <= V(i,j)- V_B(i,j) + 1;
% sums_A(:, i) + 1 <= exp(V(i,j))*(V(i,j)- V_B(i,j) + 1);
end
%约束4
for i = 1:Smax
for j = 1:N
{1,u(i,j),t(i,j)} == rotated_lorentz(1);
{u(i,j),t(i,j),Z(i,j)} == exponential(1);
log(1 + (Z_B(i,j) - V_B(i,j)))/log(2)...
+ (Z_B(i,j) - V_B(i,j))/(1 + (Z_B(i,j) - V_B(i,j)))*log(2)...
* (Z(i,j) - Z_B(i,j) - V(i,j) + V_B(i,j)) >= M(i,j);
end
end
This is the constraint 4 error.
错误使用 .* (line 173)
Disciplined convex programming error:
Cannot perform the operation: {real affine} ./ {real affine}
出错 ./ (line 19)
z = times( x, y, ‘./’ );
出错 * (line 36)
z = feval( oper, x, y );
出错 / (line 15)
z = mtimes( x, y, ‘rdivide’ );
出错 cvx_update_P (line 55)
+ (Z_B(i,j) - V_B(i,j))/(1 + (Z_B(i,j) - V_B(i,j)))*log(2)…