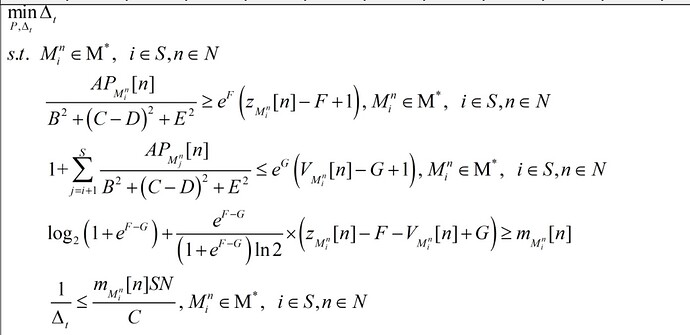HOW CAN I solve the issue “Cannot perform the operation: {log-affine} .* {real affine} ”

22

I tried to rewrite this target problem and function and defined Z_B and V_B from the previous simulation as expression variables, which successfully solved the constraint non-conformity problem mentioned above, but I encountered a new problem.My simulation result is Status: Infeasible
Optimal value (cvx_optval): +Inf.
not quite sure what went wrong.

I used the cvx+mosek solver to solve my problem (simplified as you said), and my objective problem is the following, where ABCDEFG are all numerical variables, Z, V, P, and m are the variables to be optimized, and deltaTT is the objective problem to be minimized

2
21392×676 79.6 KB

23

Here is my simulation program

function [delta_TT, P] = cvx_update_P(rou, r, H, Smax, N, num_SNs, citys, Xur, M_star, Pmax, re, Tth)

cvx_begin

variable P(Smax,N)
variable M(Smax,N)
variable Z(Smax,N)
expression Z_B(Smax,N) 
variable t(Smax,N)  
variable u(Smax,N)
variable V(Smax,N)
expression V_B(Smax,N)   
expression sums_A(1,N)
variable delta_T(Smax,N)
variable delta_TT(1,1)
minimize(delta_TT)
subject to
%约束2
for i = 1:Smax
    for j = 1:N
        city_indices = M_star(i, j); % 获取第i个城市的序号
        x_coordinates = citys(city_indices, 1); % 获取城市的坐标
        y_coordinates = citys(city_indices, 2);
        (rou*P(i,j))/(H^2 + (Xur(r,j) - x_coordinates)^2 + y_coordinates^2) >= Z(i,j) - Z_B(i,j) + 1;
        {1,u(i,j),t(i,j)} == rotated_lorentz(1);
        {u(i,j),t(i,j),Z(i,j)} == exponential(1);
    end
end

%约束3

for i = 1:Smax
    for j = 1:N
        city_indices = M_star(i, j); % 获取第i个城市的序号
        x_coordinates = citys(city_indices, 1); % 获取城市的坐标
        y_coordinates = citys(city_indices, 2);
        A(i, j) = (rou*P(i,j))/(H^2 + (Xur(r,j) - x_coordinates)^2 + y_coordinates^2);
    end
end
for i = 1:Smax
    for j = 1:N
        sums_A(j) = A(2,j) + A(3,j); % 计算每列的第二个和第三个元素的和
    end
end
for i = 1:Smax
    for j = 1:N
    {1,u(i,j),t(i,j)} == rotated_lorentz(1);
    {u(i,j),t(i,j),V(i,j)} == exponential(1);
    sums_A(j) + 1 <= V(i,j)- V_B(i,j) + 1;
    end 
end
    
%约束4
for i = 1:Smax
    for j = 1:N
        {1,u(i,j),t(i,j)} == rotated_lorentz(1);
        {u(i,j),t(i,j),Z(i,j)} == exponential(1);
        log(1 + (Z_B(i,j) - V_B(i,j)))/log(2)...
            + (Z_B(i,j) - V_B(i,j))*inv_pos((1 + (Z_B(i,j) - V_B(i,j)))*log(2))...
            * (Z(i,j) - Z_B(i,j) - V(i,j) + V_B(i,j)) >= M(i,j)  
    end
end

%约束5
for i = 1:Smax
    for j = 1:N
        re * Tth / N * inv_pos(delta_T) <= M(i,j);
    end
end

%约束6
for i = 1:Smax
    for j = 1:N
        P(i,j) >= 0;
        P(i,j) <= Pmax;
    end
end    

for i = 1:Smax
    for j = 1:N
        delta_TT  == sum(delta_T(:, i));
    end
end

cvx_end

end

24

Follow the advice in Debugging infeasible models - YALMIP , all of which except for secrtio1 also applies to CVX.