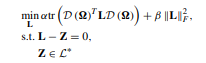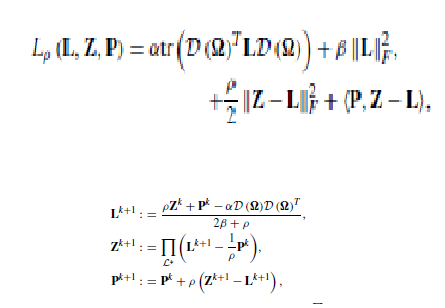I have a problem where I need to implement ADMM approach on a given cost function.
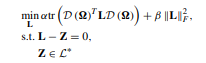
L is a Graph Laplacian Matrix
This is minimized subjected to L such that L satisifes the constraints
- Symmetric
- Positive Semi-definite
- Off-diagonal entries must be <=0 (meaning negative)
- trace(L)=N (N is the dimension of the Laplacian)
- L.1=0 (L multiplied by all ones vector must result in a zero vector) which means sum of each row in a Laplacian results in 0.
The above cost function has been implemented using ADMM approach and has been shown below
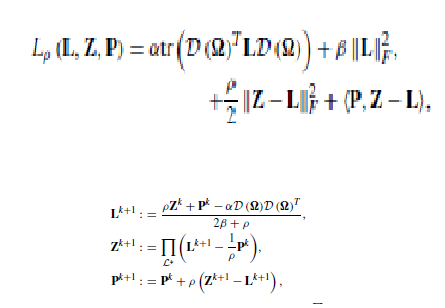
Thye Z equation has a term called Euclidean Projection which is a Frobenius norm of the difference between P and Z
The frobenius norm is minimized subjected to the properties in the Laplacian. Z is a dummy variable introduced here which has the same properties as L.
I have a trouble in implementing this Euclidean Projection
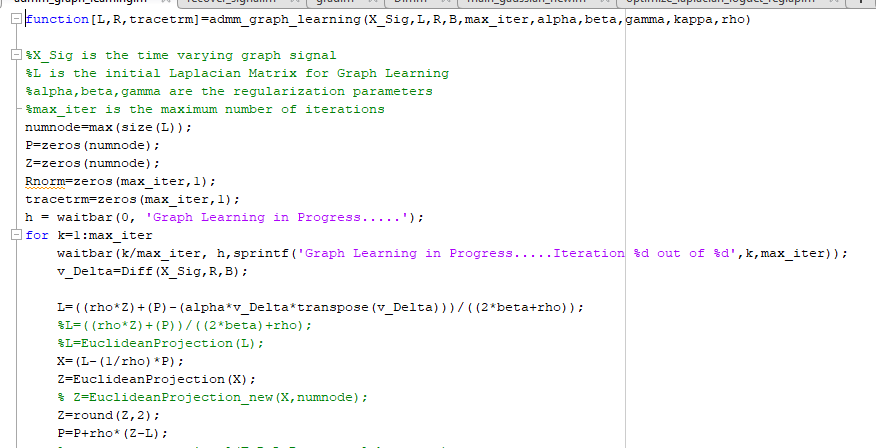
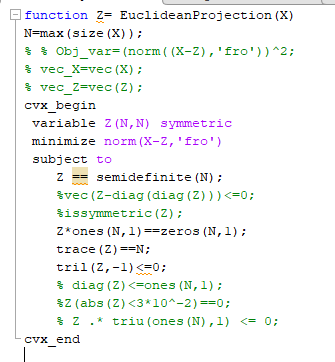
Here is my snippet where I have implemented
The Euclidean Projection function is shown below with the constraints

I have made the optimization sdp (semidefinite) declared the variable symmetric and fed the other constraints.
My expected output should be that the L matrix has to have diagonal entries as close to 1 as possible and the off diagonal entries have to be negative and sparse and they must sum up to their corresponding diagonal entry (1). The matrix has to be sparse
However when I was testing this on a weather data matrix from which I need to infer a valid Laplacian. I have got a matrix that has diagonal entries as 1 and some off diagonal entries are positive. Plus it is not sparse.
I tried another method of feeding the constraints. A method suggested in another paper they have implemented using the concept of Half Vectorization. As per their implementation my L matrix satisifes the properties but the diagonal entries are very bad.
Kindly advise me on this issue.
Despite invoking sdp mode, the program does not constrain Z (or anything else) to be positive semidefinite. There are multiple ways of doing that, to include declaring Z as semidefinite, rather than as symmetric (in which case you don’t even need sdp mode). If you want to constrain off-diagonal elements to be <= 0, one way is with the constraint tril(Z,-1) <= 0 (which is a little simpler than your commented out constraint).
Perhaps you should check the rest of your program to make sure it specifies what you intend.
Note: I inadvertently omitted the -1 from tril` in in preceding post (now corrected)…
Just want to double check. Does declaring Z semidefinite and adding the constraint tril(Z)<=0 still make Z symmetric? Please let me know.
I tried to implement by adding the tril(Z)<=0 but it has given me an error saying
Disciplined convex programming error:
Illegal operation: {invalid} - {real affine}
I have 100 iterations and this function fails in the 2nd iteration
variable Z(N,N) semidefinite
constrains Z to be symmetric positive semidefinite.
tril(Z,-1) <= 0
constrains the lower off-diagonal elements to be <= 0. Due to symmetry, that will also constrain the upper off-diagonal elements to be <= 0.
Note that I inadvertently omitted the -1 from tril in my preceding post (now corrected)…
Try again using tril(Z,-1) <= 0, as without the -1, the diagonal is being constrained to be <= 0, which is not the right thing to so.
Presumably, the invalid is because a previous iteration failed, resulting in CVX populating variables with NaN, which if used as input data, CVX considers to be invalid.
yeah in the 1st iteration I am gettin NaNs. I again tried implementing tril(Z,-1) and I still get those NaNs.
L starts with all zero matrix and keeps updating in every iteration based on the this Euclidean Projection function and the aforementioned steps.
Don’t use the quiet option, and look at the CVX and solver output, so you will know why you are getting NaN.

I have tried many ways to implement but I am not getting the desired results. Here are the ways
-
I tried using the way it is shown in the snapshot and I am getting off diagonal elements positive.
-
I tried to use vec(Z-diag(diag(Z))<=0 which satisifes the properties of the Laplacian but the entries are not the expected ones
-
tril(Z,-1) gives me NaNs
Is there any other way where I could feed in the constraints or is my dataset itself wrong? I am confused
Also the matrix Laplacian that I get is not positive semidefinite. Some eigen values are negative and
[~,p]=chol(L) gives me a non-zero value.
Here is the dataset that I am using
I think tril(Z,-1) <= 0 is getting interpreted as an SDP constraint. Try the program, including all the desired constraints, but don’t use sdp mode.
As for negative eigenvalues, if they are of magnitude < 1e-8, that is within solver tolerance.
It works but however I am still not able to obtain the expected graph laplacian. Plus
[~,p]=chol(L) always gives me non-zero value which means its not positive semidefinite.
These are my diagonal elements
0.0100
3.6700
0.0100
0.0200
0.0100
0.0100
-0.0010
0.0100
3.6700
0.0100
0.0100
0.1100
-0.0000
8.5209
8.5209
0
0.0100
0.1100
0.1400
-0.0000
-0.0000
0.1400
0.0100
0.0100
-0.0000
Latest update of my function
I dont know if there is anything wrong with my cvx usage or the data itself
If you can’t tolerate “solver tolerance” level negative eigenvalues, either
Adjust the eigenvalues to some minimum desired value after optimization is complete
or
Z - small_positive_number*eye(N) == semidefinite(N)
where small_positive_number is perhaps 1e-5 or 1e-6. That way, the optimal Z will be strictly positive definite, even allowing for solver tolerance.
-0.0072
-0.0010
-0.0000
-0.0000
-0.0000
-0.0000
-0.0000
-0.0000
0.0038
0.0096
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0100
0.0109
0.0200
0.0262
0.2100
0.2704
7.3472
17.0308
These are my eigenvalues.
[~,p]=chol(L). p still gives me a non-zero number 7
Did you do this
Z - 1e-5*eye(N) == semidefinite(N)
instead of
Z == semidefinite(N)
Yeah I have tried that but it didnt work. Got the same output as before
Thank you Dr, Mark. It was my mistake I apologize. I am getting p=0 which means semidefinite however my Laplacian’s off diagonal entries are still non-negative.
my latest function
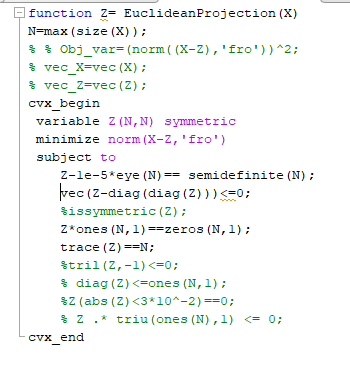
I think vec(Z-diag(diag(Z))) <= 0 should work, although it might allow off-diagonal elements not satisfying that by solver tolerance (perhaps about 1e-8). Also, it might be a bad way of entering the constraint.
You haven’t shown the output, so I don’t know what you’re saying the result was. Were there off-diagonal elements > 1e-6? I don’t think that should happen unless CVX reports Inaccurate/solved.
Have you tried tril(Z,-1) <= 0? Perhaps make it tril(Z,-1) <= -1e-6 if you want to guarantee the off-diagonal elements can’t even be slightly positive.
If you’re talking about some matrix other than Z having positive off-diagonal elements, that’s a different story.
L =
Columns 1 through 12
0.2700 0 0 0 0 0 -0.0100 -0.0200 0 0 -0.0100 -0.0100
0 2.8000 -0.0100 -0.0100 -0.0200 -0.0100 0 0 -2.6400 0 -0.0100 -0.0100
0 -0.0100 0.2300 -0.0800 -0.0300 -0.0100 0 0 -0.0200 0 -0.0100 -0.0100
0 -0.0100 -0.0800 0.3300 -0.0600 -0.0300 0 0 -0.0100 0 0 0
0 -0.0200 -0.0300 -0.0600 0.2599 -0.0400 0 0 -0.0200 0 0 0
0 -0.0100 -0.0100 -0.0300 -0.0400 0.1528 0 0 -0.0100 0 0 0
-0.0100 0 0 0 0 0 0.1300 -0.0200 0 -0.0100 0 0
-0.0200 0 0 0 0 0 -0.0200 0.2700 0 -0.0100 0 0
0 -2.6400 -0.0200 -0.0100 -0.0200 -0.0100 0 0 2.8100 0 -0.0100 -0.0100
0 0 0 0 0 0 -0.0100 -0.0100 0 0.1500 0 0
-0.0100 -0.0100 -0.0100 0 0 0 0 0 -0.0100 0 0.2400 -0.0700
-0.0100 -0.0100 -0.0100 0 0 0 0 0 -0.0100 0 -0.0700 1.1400
0 0 0 0 0 0 0 0 0 0 0 0
-0.0300 0 0 0 0 0 -0.0100 -0.0200 0 -0.0100 0 -0.0100
-0.0300 0 0 0 0 0 -0.0100 -0.0200 0 -0.0100 0 -0.0100
0 0 0 0 0 0 0 0 0 0 0 0
0 -0.0100 -0.0200 -0.1000 -0.0400 -0.0400 0 0 -0.0100 0 0 0
0.0072 -0.0300 -0.0100 0 -0.0100 0 0 0 -0.0200 0 -0.0700 -0.9700
-0.1000 0 0 0 0 0 -0.0100 -0.0400 0 0 0 0
0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 -0.0300 -0.0100 0 -0.0100 0 0
-0.0300 0 0 0 0 0 -0.0100 -0.1100 0 -0.0100 0 0
0 -0.0200 -0.0200 -0.0100 -0.0100 -0.0100 0 0 -0.0200 0 -0.0200 -0.0100
0 0 0 0 0 0 -0.0100 -0.0100 0 -0.0800 0 0
0 0 0 0 0 0 -0.0100 0 0 0 0 0
Columns 13 through 24
0 -0.0300 -0.0300 0 0 0.0072 -0.1000 0 0 -0.0300 0 0
0 0 0 0 -0.0100 -0.0300 0 0 0 0 -0.0200 0
0 0 0 0 -0.0200 -0.0100 0 0 0 0 -0.0200 0
0 0 0 0 -0.1000 0 0 0 0 0 -0.0100 0
0 0 0 0 -0.0400 -0.0100 0 0 0 0 -0.0100 0
0 0 0 0 -0.0400 0 0 0 0 0 -0.0100 0
0 -0.0100 -0.0100 0 0 0 -0.0100 0 -0.0300 -0.0100 0 -0.0100
0 -0.0200 -0.0200 0 0 0 -0.0400 0 -0.0100 -0.1100 0 -0.0100
0 0 0 0 -0.0100 -0.0200 0 0 0 0 -0.0200 0
0 -0.0100 -0.0100 0 0 0 0 0 -0.0100 -0.0100 0 -0.0800
0 0 0 0 0 -0.0700 0 0 0 0 -0.0200 0
0 -0.0100 -0.0100 0 0 -0.9700 0 0 0 0 -0.0100 0
0.0900 0 0 -0.0100 0 0 0 -0.0300 -0.0100 0 0 0
0 5.6700 -5.5301 0 0 0 -0.0200 0 0 -0.0200 0 -0.0100
0 -5.5301 5.6872 0 0 0 -0.0200 0 0 -0.0200 0 -0.0100
-0.0100 0 0 0.0400 0 0 0 0.0072 0 0 0 0
0 0 0 0 0.2599 0 0 0 0 0 -0.0100 0
0 0 0 0 0 1.1700 0 0 0 0 -0.0200 0
0 -0.0200 -0.0200 0 0 0 1.3200 0 0 -1.0800 0 0
-0.0300 0 0 0.0072 0 0 0 0.1200 -0.0100 0 0 0
-0.0100 0 0 0 0 0 0 -0.0100 0.1000 0 0 -0.0100
0 -0.0200 -0.0200 0 0 0 -1.0800 0 0 1.3100 0 -0.0100
0 0 0 0 -0.0100 -0.0200 0 0 0 0 0.1528 0
0 -0.0100 -0.0100 0 0 0 0 0 -0.0100 -0.0100 0 0.1500
-0.0200 0 0 0 0 0 0 -0.0500 -0.0100 0 0 0
Column 25
0
0
0
0
0
0
-0.0100
0
0
0
0
0
-0.0200
0
0
0
0
0
0
-0.0500
-0.0100
0
0
0
0.1200
It’s rather confusing what I’m looking at. Exactly which elements of Z violate the constraints by more than solver tolerance? And I also don’t know what you ran.
You will find it easier to get help if you show matched sets of what you ran and the corresponding results, making clear what is what.