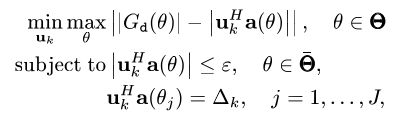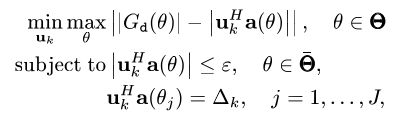
I have tried to solve this problem using this code-
cvx_begin
** variable u(N,1) complex**
** minimize(max(abs(conj(u’)a)))*
** subject to**
** conj(u’)at == 1 ;*
** conj(u’)aj == 0.01 ;*
cvx_end
But not getting the required results
Your formulation does not look even close to the image. It seems to correspond to the optimization problem at How can i solve the min-max convex optimization question . which is a different problem.
I can’t tell you what the correct formulations is, for the problem in the image (in your question in this thread) or even whether the problem is convex, because I have no idea what a(theta) or G_d(theta)` are. Do you know what they are? Have you proven the problem is convex? The convexity of the objective looks rather dubious.
This is my complete -
theta_radar_i = -10;
theta_radar_f = 10;
theta_increment = 1;
theta_radar = theta_radar_i:theta_increment:theta_radar_f;
LB = 2;
K = 2^(LB);
theta_cooms1 = -90:theta_increment:theta_radar_i-theta_increment;
theta_cooms2 = theta_radar_f+theta_increment:theta_increment:90;
theta_comms = [theta_cooms1 theta_cooms2];
theta = -90:theta_increment:90;
theta0_j = -50;
N = 10; %number of array elements
c = 3e8;
fc = 2e9;
lambda = c/fc;
d = lambda/2;
delta1 = [0.01 0.0033 0.0066 10e-4].^(1/2);
epsilon = sqrt(0.01);
n = 0:N-1;
a = exp(-1i2pid/lambda.n’.sind(theta_radar));
theta_t = 0;
theta_j = -40;
at = exp(-1i2pid/lambda.nsind(theta_t)).‘;
aj = exp(-1i2pid/lambda.nsind(theta_j)).';
ap = exp(-1i2pid/lambda.*n’.*sind(theta_comms));
Gd = exp(-1ipisind(theta_radar));
cvx_begin
variable u(N) complex
minimize((max(abs(Gd-conj(u’)*a))))
subject to
abs(conj(u’)ap) <= epsilonones(length(theta_comms),1)’ ;
conj(u’)*aj == delta1(3);
cvx_end
I have taken from a paper, In that paper it is clearly written that it is a convex problem.
it looks like you are using a toolbox function to prepare input data.
In any event, apparently theta is just a discrete set of values, and not a continuous optimization variable. Therefore, the problem is convex, and the CVX code is straightforward. I can’t speak as to the “correctness” of your input data.
I want to solve this problem using Interior Point Method. So is it possible to change the solver from default to Interior point method in CVX Toolbox?
All the solvers which can be called from CVX 2.2 use an interior point method, of one type or another. You can use cvx_solver to change the solver or change the default solver.