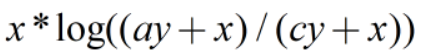
how to be expressed by cvx?
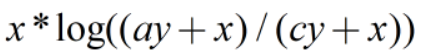
how to be expressed by cvx?
Assume
\begin{array}{l}
A = ay + x,\\
B = cy + x,\\
\therefore x\log \left( {\frac{{ay + x}}{{cy + x}}} \right) = \left( {\frac{{A - \frac{a}{c}B}}{{1 - \frac{a}{c}}}} \right)\log \left( {\frac{A}{B}} \right)
\end{array}
then you have terms like B\log \left( {\frac{A}{B}} \right) and A\log \left( {\frac{A}{B}} \right), those two can be expressed by -rel_entr(B,A) and rel_entr(A,B) respectively, then replace A and B back with the equations above. It might work.
@jackfsuia Very nice. This will be accepted by CVX as a concave expression.
1/(1-a/c)*(rel_entr(a*y+x,c*y+x)+a/c*rel_entr(c*y+x,a*y+x))
This would also work as a convex expression if 0 < a < c.
Very beautiful.that is great. Thank you very much.