Hi
I have a problem with my optimization program. I have created a simple explanation for you, which I have attached.
\min\limits_{p_1,p_2} trace ((P^{\frac{-T}{2}}{k|k-1}W_kP^{-\frac{1}{2}}{k|k-1}+C^{T}{k}(R^{\frac{-T}{2}}{k}S_kR^{-\frac{1}{2}}{k})C{k})^{-1})\
{subject~to}~ \
1=<p_1<2\
1=<p_2<2\
where W_k and S_k are diagonal matrices such that
W_k=diag(\frac{|e_k|^{p_1}+\sigma^2}{e_k^2+\sigma^2})\
S_k=diag(\frac{|f_k|^{p_2}+\sigma^2}{f_k^2+\sigma^2})\
e_k and f_k are known and ranging from (-\infty,\infty), and \sigma^2 is a very small known number.
I do not know how to write W and S matrices because cvx does not support pow(a,x) when a is constant and x is variable.
I would like to ask you, if it is possible, please guide me.
Does using
a^x = exp(x*log(a))
help you? CVX will accept the RHS if a > 0 and x is a variable or convex expression.
But your first task is to prove that your optimization problem is convex.
Thank you for your answer.
In my optimization “a” is equal to “e_k” and f_k that they may get zero, but because of
σ^2 we do not face infinity. W and S matrices in each iteration take new value and they are constant.
yes, my optimization is convex.
Actually, you can directly enter a^x in CVX, without resorting to exp(x*log(a)).
You can do
if a > 0
something = a^x +sigma_squared;
else
something = sigma_squared;
end
That is allowed because a is not a CVX variable or expression. “CVX” never even “knows” that you used an if.
You claim, without showing the proof, the problem is convex. So I leave it to you finish the CVX program. Even if it is convex, that doesn’t mean a CVX formulation.necessarily exists.
Thanks.
do you mean I can use a^x command in cvx without problem, if my problem is convex?
Since thare is abs() for e_k and f_k, they are positive. so I cannot understand what you say in
if a > 0
something = a^x +sigma_squared;
else
something = sigma_squared;
end
Moreover, in a^x= exp(x*log(a)) a get zero what do I do?
Thank you for your time.
CVX will accept a^x if a is input data (not a CVX expression) and > 0 , and x is a convex expression (of which affine is a special case). You can use exp(x*log(a)) if you prefer.
I thought you were worried about the possibility that a = 0. My if ... else ... end code deals with that.`
Thank you agin for your time and consideration. I will check it.
Is there any way to approimate a^x instead of using log?
Due to some values of e and f I fIace Inf and NAN in my optimization(because of rel_entr).
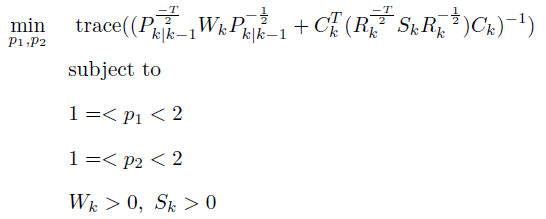
Where P_{k|k-1} and R_k are known positive definite matrices, and C_k is a known matrix. W_k and S_k are diagonal matrices such that
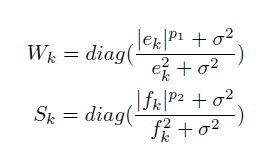
e_k and f_k are known scalar ranging from (-\infty,\infty).
Please show your complete program, preferably with all input data, and solver and CVX output.
I work on my simple code.
This is my code:
inputs:
where j1(1,1) =-4.59and j1(2,1) =10.16 are equivalent to" f" and j2(1,1) =1e-15 to j2(4,1) =1e-15 are equivalent to “e” in my previous formulation
code:
with conditions w>0 and s>0
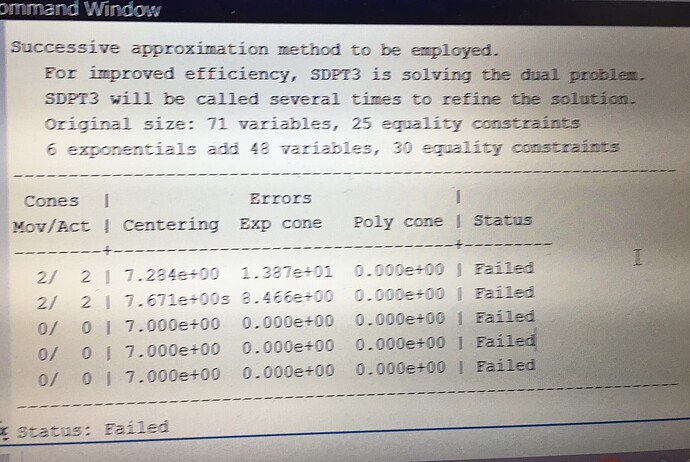
output of cv fo these initial values
with optimal value : nan
this happen because p2+rel_entr(t2)= inf to p2+rel_entr(t5)= inf due to initial value.
thanks for your consideration.
Please copy and paste your code, with inputs, using Preformatted text icon.
here is my code
%%% inputs
j1=[-4.5911;10.1629];
j2=[0;0;0;0];
p = [0.2826 -0.0000 -0.1408 0.0000;
-0.0000 0.2826 0.0000 -0.1408;
-0.1408 0.0000 0.4217 -0.0000;
0.0000 -0.1408 -0.0000 0.4217];
Rc = [5.7735 0 0 0;
0 5.7735 0 0;
0 0 0 0;
0 0 0 0];
H = [1 0 0 0;
0 1 0 0];
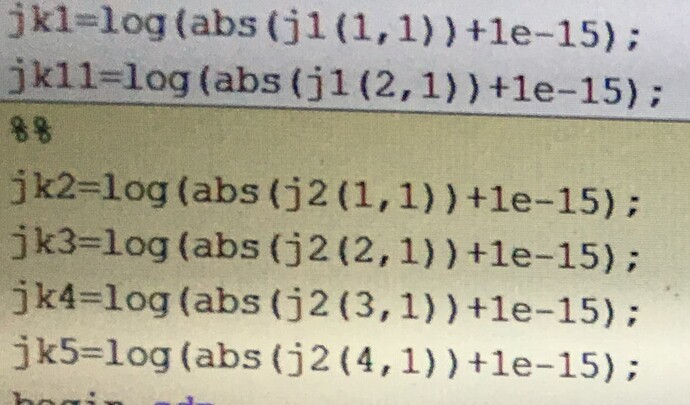
jk1=log(abs(j1(1,1))+1e-15);
jk11=log(abs(j1(2,1))+1e-15);
%%%
jk2=log(abs(j2(1,1))+1e-15);
jk3=log(abs(j2(2,1))+1e-15);
jk4=log(abs(j2(3,1))+1e-15);
jk5=log(abs(j2(4,1))+1e-15);
%%%
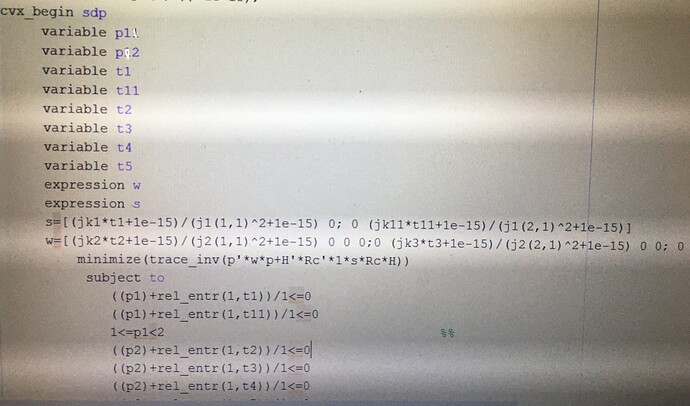
cvx_begin sdp
variable p1
variable p2
variable t1
variable t11
variable t2
variable t3
variable t4
variable t5
expression w125
expression w126
w125=[(jk1*t1+1e-15)/(j1(1,1)^2+1e-15) 0; 0 (jk11*t11+1e-15)/(j1(2,1)^2+1e-15)];
w126=[(jk2*t2+1e-15)/(j2(1,1)^2+1e-15) 0 0 0;0 (jk3*t3+1e-15)/(j2(2,1)^2+1e-15) 0 0; 0 0 (jk4*t4+1e-15)/(j2(3,1)^2+1e-15) 0;0 0 0 (jk5*t5+1e-15)/(j2(4,1)^2+1e-15)];
minimize(trace_inv(p'*w126*p+H'*Rc'*1*w125*Rc*H))
subject to
((p1)+rel_entr(1,t1))/1<=0
((p1)+rel_entr(1,t11))/1<=0
1<=p1<2 %%
((p2)+rel_entr(1,t2))/1<=0
((p2)+rel_entr(1,t3))/1<=0
((p2)+rel_entr(1,t4))/1<=0
((p2)+rel_entr(1,t5))/1<=0
1<=p2<2
w125>0
w126>0
cvx_end
j1 and j2 come from another sub-function. but for one iteration I put their values.
thanks.The additive 2nd term inside trace_inv has incompatible dimensions. For instance H' is 4 by 2 , and is multiplied by Rc, which is 4 by 4. So MATLAB (not even CVX) produces an error message, as it should, just based on double precision data. So I don’t know how you even got anything to run. Perhaps the inputs you ran are different than what’s in your post?
Also, your output shows CVX’s (unreliable) Successive Approximation method was used. You should use Mosek as solver if available, in which case Mosek’s native exponential cone capability will be used. if Mosek is not available to you, follow the instructions at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions .
Sorry, when I copied and tried to set them unfortunately the size of Rc has changed. its real Rc is
Rc = [5.7735 0;
0 5.7735]
Moreover, I have used a^x=exp(log a*x) as it is eplained in cvxquad and you explained. For example this command log(abs(j1(1,1))+1e-15) is equivalent to log( a ) and its relevant constriants ((p1)+rel_entr(1,t1))/1<=0…,
but these commands ((p2)+rel_entr(1,t2))<=0…((p2)+rel_entr(1,t5)) are not satisfied for initial value of j2 and t4,t5…= inf
sorry again for confusing you.
I ran it in Mosek, which reported Infeasible.
There is an incompatibility (i.e., infeasibility) among the combination of constraints:
((p2)+rel_entr(1,t2))/1<=0
((p2)+rel_entr(1,t3))/1<=0
((p2)+rel_entr(1,t4))/1<=0
((p2)+rel_entr(1,t5))/1<=0
1<=p2<2
w126>0
If 1<=p2<2 is removed, the problem is feasible and solves to reported optimality. When I ran it (with Mosek 10.0.45 as solver), the optimal value assigned to p2 = -32.
I can’t tell you what you should do with your problem. However, the combination of the problem specification and input data is infeasible.