Hi,
I am new to CVX and I might not be used to DCP format.
I am having a problem writing down a constraint in CVX.
I would really appreciate it if somebody could see how to solve.
I need to write down this constraint in CVX.
Since CVX rejects quadratic form of matrix, I have managed to change trace into sum_square_abs without quadratic form of matrix.
However, I have no idea how to deal with ‘log_det(Q*Q’)’.
Is there anyway that I can write this without quadratic form of matrix?
Since I am not good at this, it might be easy problem, but I would really appreciate it
if someone suggest some methods.
Thank you
Hope you all doing well in the situation.
Does Q ever appear in your problem other than in the form Q*Q'? If not, then declare QQH as a CVX variable and use log_det(QQH), which CVX will accept (and automatically constrain to be Hermitian (if QQH is declared complex) positive semidefinite).
Thanks for your comment!.
I really appreciate it.
However, I need it to be Q*Q^H, since I also have a constraint shown below
.
In this constraint, variables are w and Q, and and I need it to be in form of ‘second order cone’ to make it convex.
So even though Q does not appear, I need to declare Q as CVX variable.
You think it’s impossible?
If you were willing to impose that Q is Hermitian psd, you could use log_det(QQ') = 2*log_det(Q). Other than that, I don’t know. Perhaps someone else has a reformulation trick.
Thank you for your suggestion!!
It would really help.
I have also tried to write down this constraint below using ‘norm’ function
However, as you might already know, norm({convex}) is rejected by CVX.
Do you happen to know other way to write it down?
Thank you again for your time spent on suggestion and comment.
I had in mind that if Q were psd, that would allow you to handle log_det(Q*Q'). That would then allow you to append Q'*h to whatever vector you would take the two-norm of in order to handle h'*Q*Q'*h term inside the sqrt.
Fortunately, Q is PSD.
However, to write
this constraint, I thought I would need other function other than ‘norm’.
Because the CVX rejects it as shown below
Thank you for keep reading my inquiries and answering them.
I really appreciate it!!
Concatenate everything inside the sqrt and before squaring, into one vector affine in its argument… Then take the norm of that. Do not take norm of norm, which as you’ve seen CVX does not allow.
So that would be concatenation of (portions of which repeated as necessary for various indices), h'*w, h'*w_tilde, Q'*h, sigma . I’ll let you work out the details and handle all the indices.
One note of concern or interest, is that if Q is psd, then why is the model written with QQ^H, rather than with Q^2, which are equal if Q is hermitian.
oh…I have told you wrong…
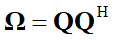
Here, Omega is PSD not Q… Sorry for the misunderstanding.
I guess your valuable suggestion would not work , would it?
Also, is the ‘norm of norm’ reason why CVX rejects this constraint?
.
I have run it without the term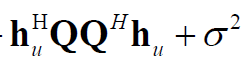 
which is inside the sqrt
as shown below.
.
However I still get message as below
oh…I have told you wrong…
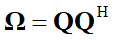
Here, Omega is PSD not Q… Sorry for the misunderstanding.
I guess your valuable suggestion would not work , would it?
Yes, I know that QQ^H is psd. If Q is not psd, we’re back to my earlier statement
If you were willing to impose that Q is Hermitian psd, you could use log_det(QQ') = 2*log_det(Q) . Other than that, I don’t know. Perhaps someone else has a reformulation trick.
The argument of norm must be affine, which norm is not. That’s why I said you should concatenate everything into one vector, affine in its argument, then take the norm of that vector.
Thank you so much.
Do you think the function of set ‘lorentz’ should be helpful for writing this constraint?
I think CVX rejects norm({convex}) format, not only norm({norm}).
Thank you for your time again.
Thank you so much.
Do you think the function of set ‘lorentz’ should be helpful for writing this constraint?
I think CVX rejects norm({convex}) format, not only norm({norm}).
Thank you for your time again.
Thank you so much.
Your help means a lot to me.
I 've got what you mean by the constraint
I guess I should deal with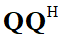 
just by multiplying each column and row one by one.
lorentz won’t allow you to do anything you can’t do with norm.
As I wrote, the argument of norm must be affine. The only convex argument of norm which is allowed is an affine argument (CVX will call that affine, not convex).
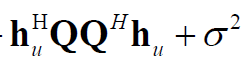which is inside the sqrt
just by multiplying each column and row one by one.