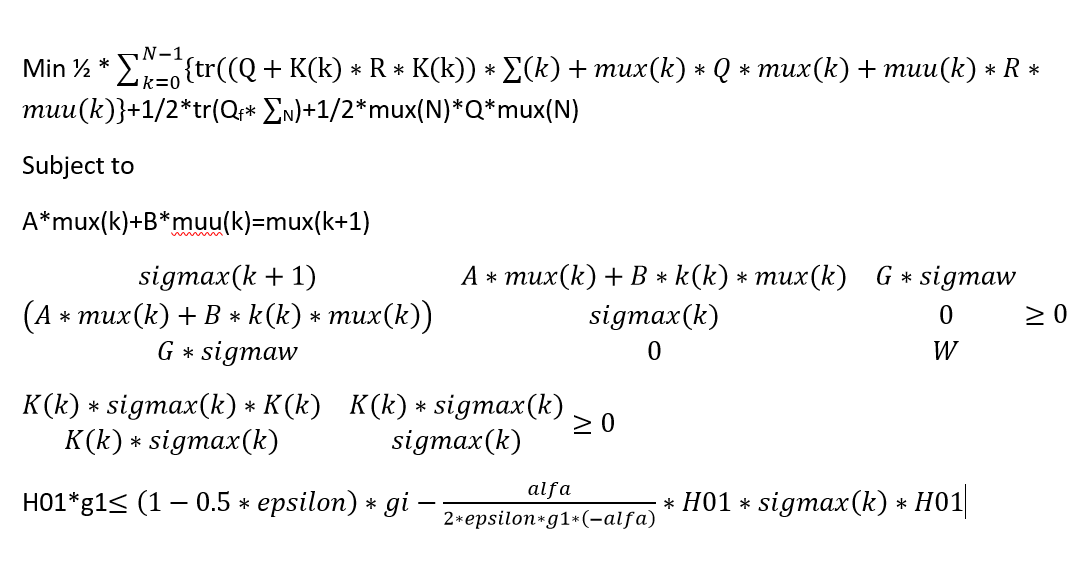I write this problem in yalmip
in this format:
clc,clear,close all
% time structure
t0=0; %intial time
tf=10; %final time
dt=0.01; %sampling time
time=t0:dt:tf-dt %time vector
Ns=length(time);
%% system structure ======> x(k+1)=A*x(k)+B*u(k)
A = [1.02 -0.1
0.1 0.98]
B = [0.5 0
0.05 0.5]
G=[0.3 0;0 0.3]
[nx nu]=size(B)
%% Mpc parameter
Q = eye(nx);
R = eye(nu)*50;
Qf = eye(nu)*50;
N=25;
sigmax=[1 0;0 1]
sigmaw=[1 0;0 1]
mux = [1;5]
h1x=[-1/sqrt(5);-2/sqrt(5)]
epsilon=0.2
g1=3
K = sdpvar(repmat(nu,1,N),repmat(nx,1,N))
muu = sdpvar (repmat(nu,1,N),repmat(1,1,N) )
sigmax = sdpvar (repmat (nx,1,N),repmat(nu,1,N))
sigmax2 = sdpvar (repmat (nx,1,N),repmat(nu,1,N))
mux = sdpvar (repmat(nu,1,N),repmat(1,1,N) )
constrant=[];
objective=0
for k=1:N;
mux{k+1}=A*mux{k}+B*muu{k}
constant2 =[ sigmax2{k} (A*sigmax{k}+B*K{k}*sigmax{k}) G*sigmaw
(A*sigmax{k}+B*K{k}*sigmax{k})' sigmax{k} zeros(2)
( G*sigmaw)' zeros(2) sigmaw]>=0
constant3 =[K{k}*sigmax{k}*K{k} (K{k}*sigmax{k})'
(K{k}*sigmax{k}) sigmax{k}]>=0
h1x<=(1-(0.5*epsilon))*g1-((0.95/2*epsilon*g1*(-0.95))*h1x'*sigmax{k}*h1x)
constrant=[constrant,constant2+constant3]
objective =objective +trace((Q+K{k}*R*K{k})*sigmax{k})+(mux{k})'*Q*(mux{k})+(muu{k})'*R*muu{k}
sigmax{k}=sigmax2{k}
end
option = sdpsettings('solver','penlab')
a=optimize (constrant,objective,option)
u= value(muu)
x=value(mux)
but my answer is zero and its incorrect.
And I want to solve with cvx but I couldent formulate in true form,how i can write this cost function in cvx ?