code1: 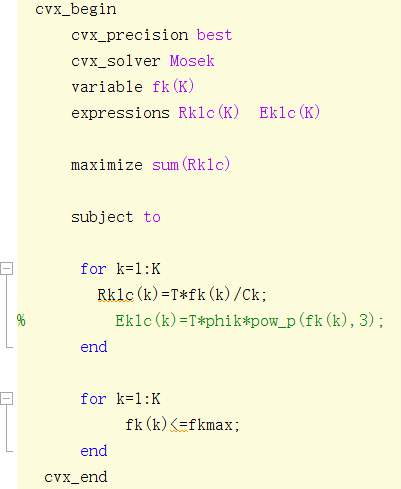
result1:
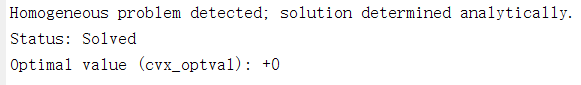
code2:

result 2:

I don’k konw what is the difference between them, cause Eklc does not interfere the optimization due to no constraint for it.
code1: 
result1:
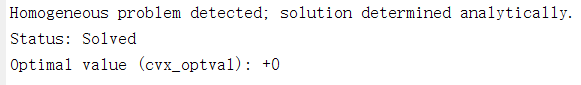
code2:

result 2:

I don’k konw what is the difference between them, cause Eklc does not interfere the optimization due to no constraint for it.
I think maybe fk^3 is a trouble, however, even though I revise it as 0<=fk(k), it is still unworked.
The objective I really want to maximize is that sum(Rklc)-eta*sum(Eklc), so this test confuse me
Never use cvx_precision best with Mosek.
Please show log output and/or fully reproducible example.
Thank you for your reminder, I have removed this command.
here, I show a simple example, i.e.,
code 1:
q=0;
K=2;
xmax=10;
cvx_begin
cvx_solver Mosek
variable x(K)
expressions fx(K) gx(K)
maximize sum(fx)
% maximize sum(fx)-q*sum(gx)
subject to
for k=1:K
fx(k)=x(k);
end
for k=1:K
0<=x(k)<=xmax;
end
cvx_end
code 2:
q=0;
K=2;
xmax=10;
cvx_begin
cvx_solver Mosek
variable x(K)
expressions fx(K) gx(K)
maximize sum(fx)
% maximize sum(fx)-q*sum(gx)
subject to
for k=1:K
fx(k)=x(k);
gx(k)=pow_p(x(k),3);
end
for k=1:K
0<=x(k)<=xmax;
end
cvx_end
The outputs of these two codes are significantly different, I cannot understand why this is. With such a result, I cannot run this objective maximize sum(fx)-q*sum(gx) at all.
The main difference between them is whether the expression gx(k) exists or not.
I don’t completely understand in what order CVX processes things but if I define all expressions before using them then the results look more reasonable. That is, for example in your 2nd code:
q=0;
K=1;
xmax=10;
cvx_begin
cvx_solver Mosek_2
variable x(K)
expressions fx(K) gx(K)
cvx_solver_settings('write', 'c2.ptf')
for k=1:K
fx(k)=x(k);
gx(k)=pow_p(x(k),3);
end
maximize sum(fx)
% maximize sum(fx)-q*sum(gx)
subject to
for k=1:K
0<=x(k)<=xmax;
end
cvx_end
Thank you for your time. I am very appreciative of your help. This code can work normally now!
CVX solves all your problems as feasibility problems. Any, even trivial, difference between CVX programs, can result in a different feasible solution being returned.
That is because you are maximizing 0, which is the default (initial) values of an expression which has not already been set equal to something. Therefore, @Michal_Adamaszek 's approach of setting the expressions before using them, in the objective function, is the (a) correct way of modeling the problem you intend.
Constraints can be specified before and/or after the objective.
subject to is a placebo which does absolutely nothing, and is intended as a visual aid for anyone wanting to use it. Use of subject to is neither necessary nor sufficient for statements to be constraints.
0<=x(k)<=xmax is a constraint.
fx(k)=x(k); is an expression assignment, and is not a constraint, despite being after subject to.
== specifies equality constraint. It is different than =, which is expression assignment.
Thanks for your reply and explanation. I have another question, how do deal with the optimization variable with a large valve, such as if its valve is more than 10^10? In this case, the output result may be wrong.
clc;
close all;
clear all;
q=0;
K=2;
Rkth=10^1;
phik=10^-26;
Ck=1000;
T=1;
for i=1:10
cvx_begin
cvx_solver SDPT3
cvx_precision best
variable fk(K)
expressions Rklc(K) Eklc(K)
for k=1:K
Rklc(k)=T*fk(k)/Ck;
Eklc(k)=T*phik*pow_p(fk(k),3);
end
% maximize sum(Rklc)
maximize sum(Rklc)-q*sum(Eklc)
subject to
for k=1:K
T*fk(k)/Ck>=Rkth;
end
cvx_end
q=sum(Rklc)/sum(Eklc);
qe(i)=q;
end
plot(1:10,qe)
For example, when variable Rkth exceeds 10^2 or larger, the output is inefficient. If I want Rkth=10^4, how to revise this code, or what content should be added?
Since fk has no upper bound. Thus, I don’t think this variable is going to be infeasible.
First of all, don’t use cvx_precision_best, whether with Mosek as @Michal_Adamaszek advised you, or with any other solver. Its incorporation in CVX was well-intentioned, but misguided
Number such as 10^-26 are generally not a good thing in optimization. You should improve numerical scaling by change units so that non-zero input data is within a small number of orders of magnitude of one. Hopefully, but not guaranteed, optimal variable values (argmax) and optimal objective value will not be too “crazy”.
If it is impossible to do such rescaling, and input values differ by many orders of magnitude, that could be problematic for double precision solvers, as all solvers called by CVX are (wit the exception of certain computations being done in quad precision in Gurobi, with some non-default Gurobi parameter settings. The “rules” for scaling might differ somewhat when log or exp are involved.
If the problem scaling is bad, the solver’s determination of infeasibility or unboundeness might not be robust, i.e., could be wrong. Or the solver could give up (fail) due to numerical difficulties. If you use Mosek, pay attention to any warnings it provides about large or near-zero input data.