Why the LP problem return "infeasible"?

1

Hello all. I am trying to solve the following algorithm however, MatLab did not return the correct result for it. Can anyone tell me what is the problem with my code?

Screenshot 2022-09-28 160718|423x499

Screenshot 2022-09-28 160628
Screenshot 2022-09-28 1606281562×1032 46.4 KB

Here, X is the N3 dimensions array. f_r is the r-th column of the eigenvector of XX^{T} which makes sure that X*X^{T} is a square matrix. V is the Vector in my code.

Here is the full code:

*close all
clear
clc

rng(‘default’)
q= rng;

tic

% Generating the sample
x = -0.5 + rand(4,1) ;
y = -0.5 + rand(4,1) ;
X4 = [];
X5 = [];
X8 = [];
X9 = [];
for i = 1:2
if ((x(i))^2 + (y(i))^2) <= 0.25
X4 = [X4,x(i)];
X5 = [X5,y(i)];
end
end

for j = 3:4
if ((x(j))^2 + (y(j))^2) <= 0.25
X8 = [X4,x(j)];
X9 = [X5,y(j)];
end
end
X6 = zeros(1,length(X4)) ;
X7 = 1 * ones(1,length(X8));

radius = 0.5 * ones(1,2);
theta = 2rand(2,1);
X1 = diag(radius) * cos(thetapi);
X2 = diag(radius) * sin(thetapi);
X3 = 1rand(2,1);

X1 = vertcat(X1,X4’,X8’);
X2 = vertcat(X2,X5’,X9’);
X3 = vertcat(X3,X6’,X7’);

X = horzcat(X1,X2,X3); % sample

%algorithm 1

S = X - mean(X,2);

S1 = S(:,1);
S2 = S(:,2);
S3 = S(:,3);

R_s = S * S’;

[Vector,Value] = eig(R_s);
Vector = real(Vector);

s = length(X);
resultX = zeros(length(X),length(X));
resultY = zeros(length(X),length(X));
resultZ = zeros(length(X),length(X));
for i = 1:s
parX = (transpose(Vector(:,i)) * X(:,1)) * (Vector(:,i));
resultX(:,i) = parX;

parY = (transpose(Vector(:,i)) * X(:,2)) * (Vector(:,i));
resultY(:,i) = parY;

parZ = (transpose(Vector(:,i)) * X(:,3)) * (Vector(:,i));
resultZ(:,i) = parZ;

end

result = zeros(length(X),length(X));

C = {};

for i = 1:length(Vector)


    res = kron(Vector(:,i),transpose(Vector(:,i)));

    for j = 1:length(Vector)

        result = res*Vector(j,i);
        C{j,i} = result;

    end

end

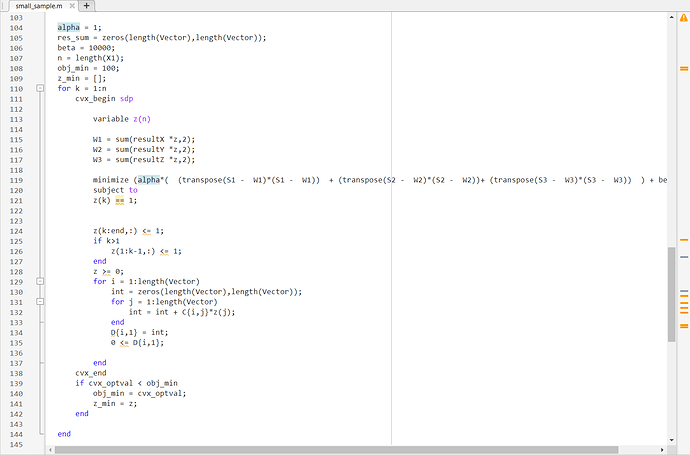
D = {};

alpha = 1;
res_sum = zeros(length(Vector),length(Vector));
beta = 10000;
n = length(X1);
obj_min = 100;
z_min = [];
for k = 1:n
cvx_begin sdp

    variable z(n)

    W1 = sum(resultX *z,2);
    W2 = sum(resultY *z,2);
    W3 = sum(resultZ *z,2);

    minimize (alpha*(  (transpose(S1 -  W1)*(S1 -  W1))  + (transpose(S2 -  W2)*(S2 -  W2))+ (transpose(S3 -  W3)*(S3 -  W3))  ) + beta*z'*z);
    subject to
    z(k) == 1;
  

    z(k:end,:) <= 1;
    if k>1
        z(1:k-1,:) <= 1;
    end
    z >= 0;
    for i = 1:length(Vector)
        int = zeros(length(Vector),length(Vector));
        for j = 1:length(Vector)
            int = int + C{i,j}*z(j);
        end
        D{i,1} = int;
        0 <= D{i,1};
       
    end
cvx_end
if cvx_optval < obj_min
    obj_min = cvx_optval;
    z_min = z;
end

end

2

I don’t think it’s relevant to your difficulty, but is there a reason you invoked sdp mode? If you use that and have a square (symmetric) matrix in an inequality constraint, you may inadvertently specify an SDP (LMI) constraint when not intended. If an optimization problem is an LP, it can’t have any SDP constraints. Although your problem actually appears to be a QP, not LP.

All but section 1 of https://yalmip.github.io/debugginginfeasible also apples to debugging infeasible in CVX.

3

Thank you very much!
Sorry for the ambiguous description. The constraint shows that it is the SDP and QP problem. The problem is that in line 121; when you remove line 121, it can be solved. line 121 means that you put 1 in the i-th for the z. The paper shows that when you declare the location of i-th element is one, it is convex problem otherwise, it is not. Even if you only keep line 121 and remove some other constrains, you can still get an “infeasible” solution.

4

Sorry, just test the constraints. The problem is on the square (symmetric) matrix. When I remove that constraint, the program works well.

5

I’m confused. Where is your matrix constraint. Maybe I’m not keeping track of what’s going on with the cells.

6

Cell contains N matrixs and each matrix is N*N. Basiclly, from line 129 to line 135, there is 3 order N * N * N tensor which the dimension is N^3.
I would like to put these constraints into cvx. From line 129 to line 135, there are N constraints, each of them is a symmetric matrix which is greater than 0. (I use N matrix to represent the tensor)
I think that I cannot add constraints like this. It is too ugly. I will try to put the computation steps below “Variable z” and leave pure matrix form in “subject to”, which I remove the ugly for loop from “subject to” and add below “Variable z(n)”.

7

I’m not sure how things work using cells, but it should be easy using 3D arrays.
variable M(5,5,3) symmetric
makes M(:,:,i) a 5 by 5 symmetric matrix for each value of i from 1 to 3.

If you actually want each of these matrices to be psd, you can instead use
variable M(5,5,3) semidefinite
and then you don’t even need any additional constraints to make all 3 of these M(:,:,i) matrices psd.

Change the numbers 5 and 3 to whatever you want.