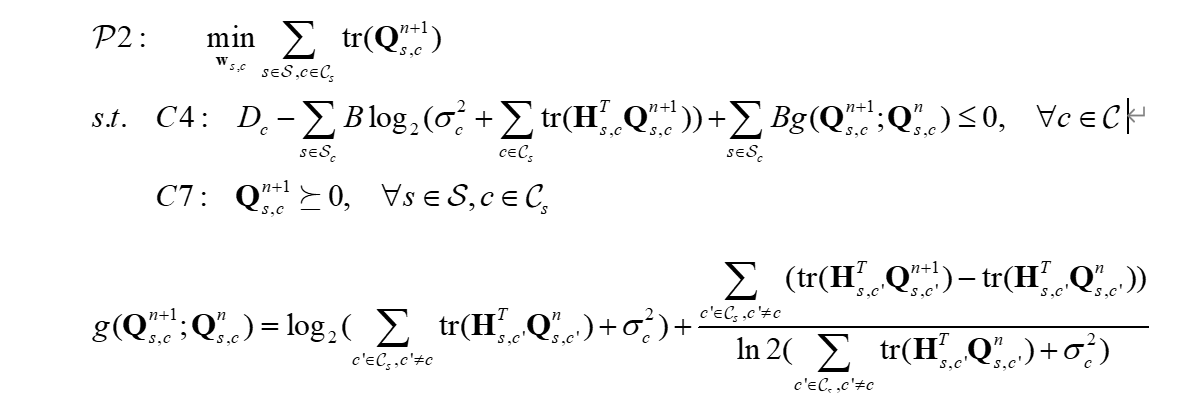I’m trying to design an algorithm based on majorization minimization (MM) method for DC programming, which iteratively solve the following convex problem.
And the cvx code and output is given as follows.
cvx_solver Mosek;
cvx_begin sdp
variable Q_new(64,64,ue_num,ser_sat_num) hermitian;
expression transmission_power_new(ue_num,ser_sat_num);
expression received_power_new(ue_num,sat_num);
expression linear_g(ue_num,ser_sat_num);
expression p2(ue_num,ser_sat_num);
minimize sum(sum(transmission_power_new));
subject to
for c=1:ue_num
for i=1:ser_sat_num
transmission_power_new(c,i)=trace(real(Q_new(:,:,c,i)));
received_power_new(c,ser_sat(c,i))=real(ChannelGain_vector_cell{ser_sat(c,i),c}'...
*Q_new(:,:,c,i)*ChannelGain_vector_cell{ser_sat(c,i),c});
linear_g(c,i)=(-rel_entr(1,N0+sum(received_power_old(:,ser_sat(c,i)))-received_power_old(c,ser_sat(c,i))))/log(2)...
+((sum(received_power_new(:,ser_sat(c,i)))-received_power_new(c,ser_sat(c,i)))...
-(sum(received_power_old(:,ser_sat(c,i)))-received_power_old(c,ser_sat(c,i))))...
./(log(2).*(N0+sum(received_power_old(:,ser_sat(c,i)))-received_power_old(c,ser_sat(c,i))));
p2(c,i)=-rel_entr(1,N0+sum(received_power_new(:,ser_sat(c,i))))/log(2);
Q_new(:,:,c,i)==hermitian_semidefinite(64);
end
demand(c)/bandwidth-sum(p2(c,:))+sum(linear_g(c,:))<=0;
end
cvx_end
Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: 0.0000000000e+00 nrm: 1e+02 Viol. con: 2e-09 var: 0e+00 barvar: 0e+00 cones: 8e-17
Dual. obj: 7.1516504217e-11 nrm: 6e+01 Viol. con: 0e+00 var: 6e-23 barvar: 2e-11 cones: 5e-11
Optimizer summary
Optimizer - time: 0.16
Interior-point - iterations : 7 time: 0.14
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00
------------------------------------------------------------
Status: Solved
Optimal value (cvx_optval): +0
But there are problems.
- The optimal value given by cvx is 0. But when I calculated the objective value with the output matrix
Q_new, I got a reasonable value. Why? - What about the convergence of MM method? My program stopped after one
or two iterations and I think the threshold to stop is set small enough. Is there something wrong with my program? Or some parameters are set improperly?
What should I do to correct my program? I would really appreciate it if someone helped.