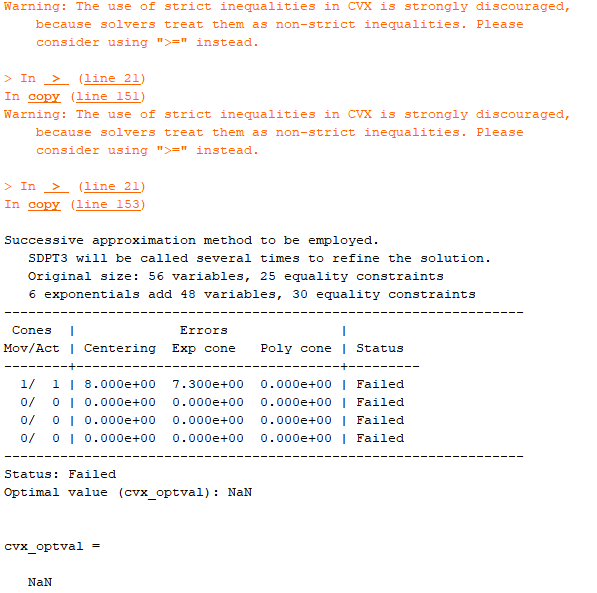
Also have the problem , why the cvx_optval always be ‘NaN’ 
clear
clc
clear cvx
M = 2 ; % Number of antenna at DFRC BS
K = 3 ; % Number of Single antenna users
N = 10 ; % Number of active RIS’s reflection
r_th = 0.3 ;
tolerance = 1e-3 ;
p_max_dbm = 40;
p_max = 10^((p_max_dbm - 30)/10);
for i = 1:1:(K+2)
P(:,i)= rand(M,1) + 1i * rand(M,1) ; %
end
theta = 2pirand(N,1) ;
phi = 1 * exp(j*theta) ; %
Phi = diag(phi) ; %
lambda_c = 1 ; %
d_R = 1 ; %
d_B = 1 ; %
theta_a = 2pirand() ; %
theta_b = 2pirand() ; %
aa = (2pi)/lambda_c * d_R * sin(theta_a) ;
bb = (2pi)/lambda_c * d_B * sin(theta_b) ;
for i = 1:1:N
a(i,1) = exp(jaa(i-1)) ; %
end
for i = 1:1:M
b(i,1) = exp(jbb(i-1)) ; %
end
beta_a = 1 ; %
beta_b = 1 ; %
A = beta_a * b * a’ ; %
B = beta_b * b * b’ ; %
G = rand(N,M) + 1i * rand(N,M) ; %
H_r = APhiG + B ; %
for i = 1:1:K
h_1(:,i) = rand(N,1) + 1i * rand(N,1) ; %
h_2(:,i) = rand(M,1) + 1i * rand(M,1) ; %
end
H_k = h_1’ * Phi * G + h_2’ ; %
plus_r = 0 ;
for i = 1:1:K %
plus_1 = P(:,i+1)’ * H_r’ * H_r * P(:,i+1) ;
plus_r = plus_r + plus_1 ;
end
sigma_r_1 = P(:,1)’ * H_r’ * H_r * P(:,1) ; %
sigma_r_2 = plus_r ; %
sigma_r_3 = 1 * norm(A*Phi)^2 ; %
sigma_r = sigma_r_1 + sigma_r_2 + sigma_r_3 + 1 ; %
rho_r = P(:,K+2)’ * H_r’ * H_r * P(:,K+2) / sigma_r ; %
for i = 1:1:K
plus_c = 0 ;
plus_p = 0 ;
for j = 1:1:K % Calculate term 1 ---
plus_1 = abs( H_k(i,:) * P(:,j+1) )^2 ;
plus_c = plus_c + plus_1 ;
if j ~= i
plus_p = plus_p + plus_1 ;
end
end
sigma_c_1(i) = plus_c ; % SINR's Denominator of commom part , term 1
sigma_p_1(i) = plus_p ; % SINR's Denominator of private part , term 1
sigma_c_2(i) = abs( H_k(i,:) * P(:,K+2) )^2 ; % SINR's Denominator of commom part , term 2
sigma_c_3(i) = h_1(:,i)' * Phi * Phi' * h_1(:,i) ; % SINR's Denominator of commom part , term 3
end
for i = 1:1:K
sigma_c(i) = sigma_c_1(i) + sigma_c_2(i) + sigma_c_3(i) + 1 ; % SINR’s Denominator of commom part
sigma_p(i) = sigma_p_1(i) + sigma_c_2(i) + sigma_c_3(i) + 1 ; % SINR’s Denominator of private part
end
for i = 1:1:K
rho_c(i) = abs( H_k(i,
* P(:,1) )^2 / sigma_c(i) ; % SINR of common part
rho_p(i) = abs( H_k(i, * P(:,1+i))^2 / sigma_p(i) ; % SINR of private part
end
isConverged = false;
t = 0 ;
% while (~isConverged)
cvx_clear
cvx_begin
variable P_var(M,K+2)
variable c(1,K)
variable R_p(1,K)
variable rho_c_var(1,K)
variable rho_p_var(1,K)
variable rho_r_var(1,1)
variable sigma_c_var(1,K)
variable sigma_p_var(1,K)
variable sigma_r_var(1,1)
maximize( sum(c + R_p) )
subject to
for i = 1:1:K
log( 1 + rho_c_var(:,i) )/log(2) >= sum(c) ; %
log( 1 + rho_p_var(:,i) )/log(2) >= R_p(:,i) ; %
end
for i = 1:1:K
sigma_c_var(:,i) >= real(sigma_c(:,i)) ; %
sigma_p_var(:,i) >= real(sigma_p(:,i)) ; %
end
for i =1:1:K
( 2*real( P(:,1)' * H_k(i,:)' * H_k(i,:) * P_var(:,1) / real(sigma_c(:,i)) ) ) - (( abs( H_k(i,:) * P(:,1) )^2 * sigma_c_var(:,i) ) / real((sigma_c(:,i))^2)) >= rho_c_var(:,i) ; % ---
( 2*real( P(:,i+1)' * H_k(i,:)' * H_k(i,:) * P_var(:,i+1) / real(sigma_p(:,i)) ) ) - (( abs( H_k(i,:) * P(:,i+1) )^2 * sigma_p_var(:,i) ) / real((sigma_p(:,i))^2)) >= rho_p_var(:,i) ;% ---
end
P_var(:,1)'*P_var(:,1) + P_var(:,2)'*P_var(:,2) + P_var(:,3)'*P_var(:,3) <= p_max ;
c + R_p >= r_th ;
c > 0 ;
R_p > 0 ;
sigma_r_var(1,1) >= real(P(:,1)' * H_r' * H_r * P(:,1) + sigma_r_2 + 1 * norm(A*Phi)^2) ;
( 2*real( P(:,K+2)' * H_r' * H_r * P_var(:,K+2) / real(sigma_r(1,1)) ) ) - ( ( real(P(:,K+2)' * H_r' * H_r * P(:,K+2) * sigma_r_var)) / real(sigma_r(1,1)^2) ) >= rho_r_var ;
cvx_end
% for i =1:1:K+2
% P(:,i) = P_var(:,i) ;
% end
%
% for i = 1:1:K
% rho_c(1,i) = rho_c_var(1,i) ;
% rho_p(1,i) = rho_p_var(1,i) ;
% end
%
% rho_r(1,1) = rho_r_var(1,1) ;
%
% t_ = cvx_optval ;
% P(:,1) = p_c ;
% P(:,2) = p_1 ;
% P(:,3) = p_2 ;
%
% rho_c_1 = rho_c(:,1) ;
% rho_c_2 = rho_c(:,2) ;
% rho_p_1 = rho_p(:,1) ;
% rho_p_2 = rho_p(:,2) ;
% t_ = cvx_optval ;
%
% if abs( t_ - t ) < tolerance
% isConverged = true;
% else
% t = t_
% end
% end
cvx_optval
