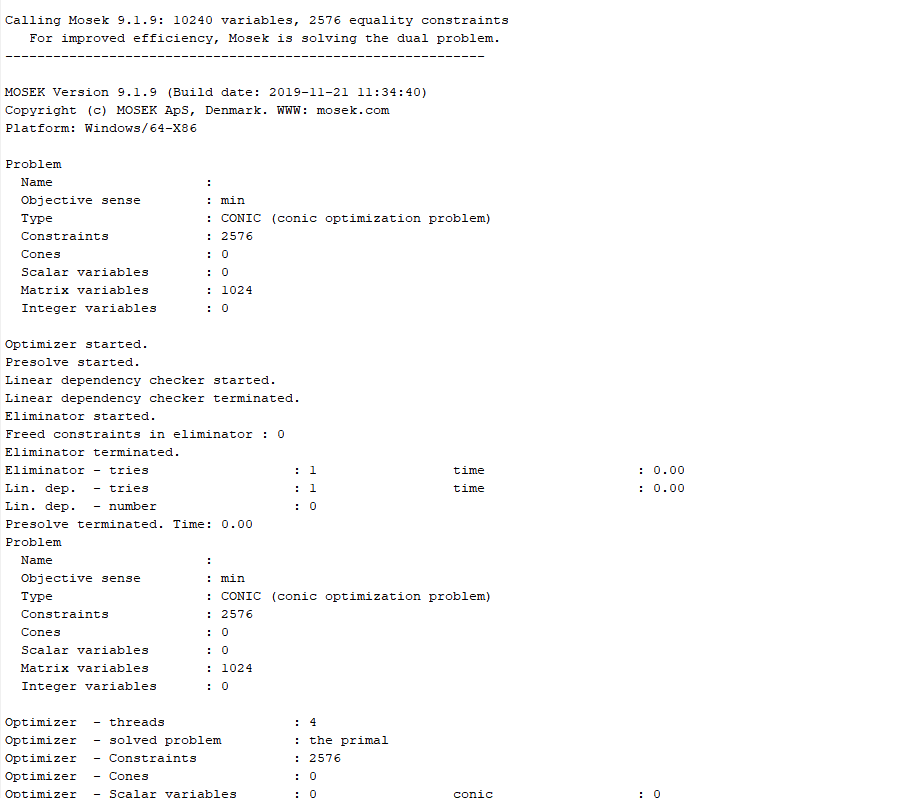
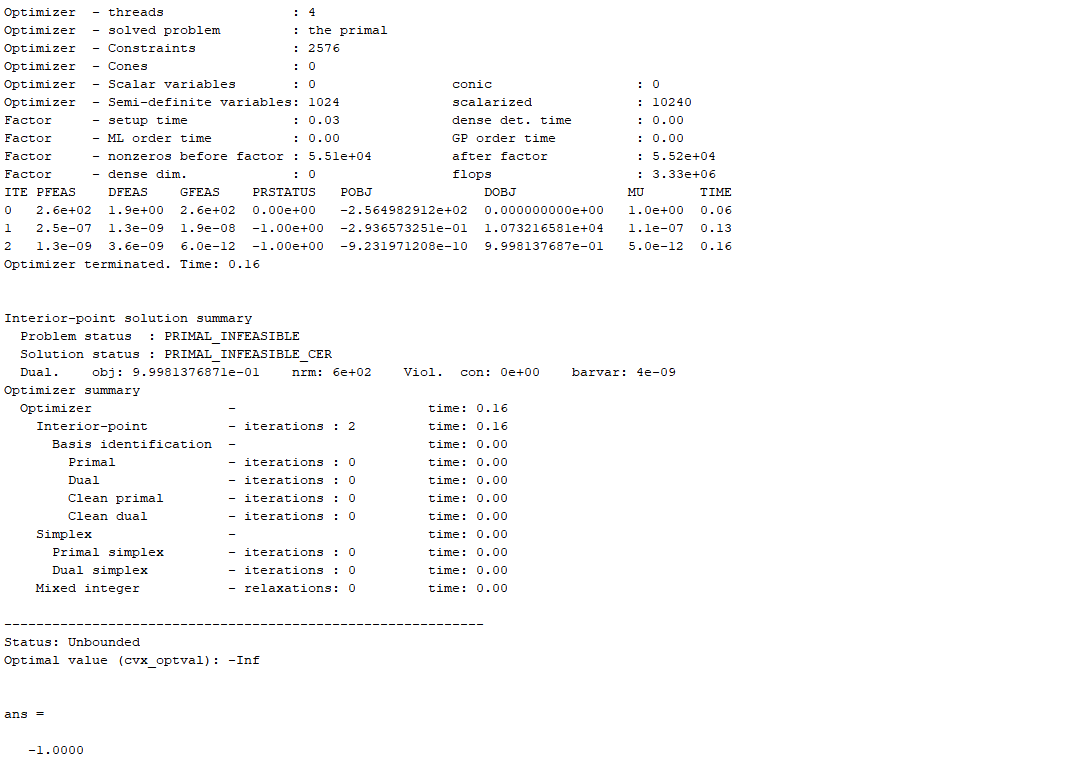
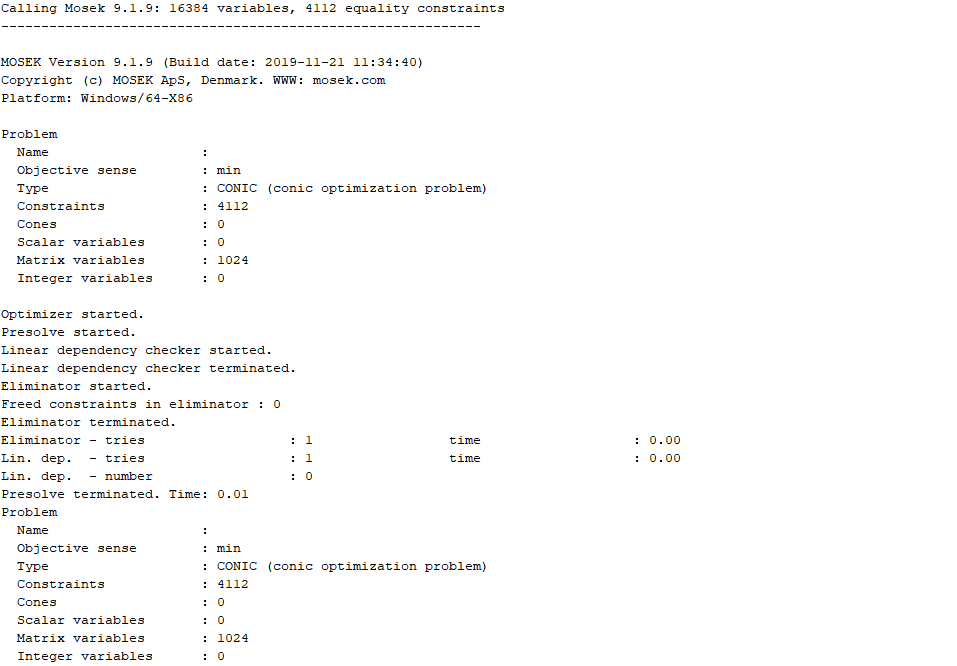
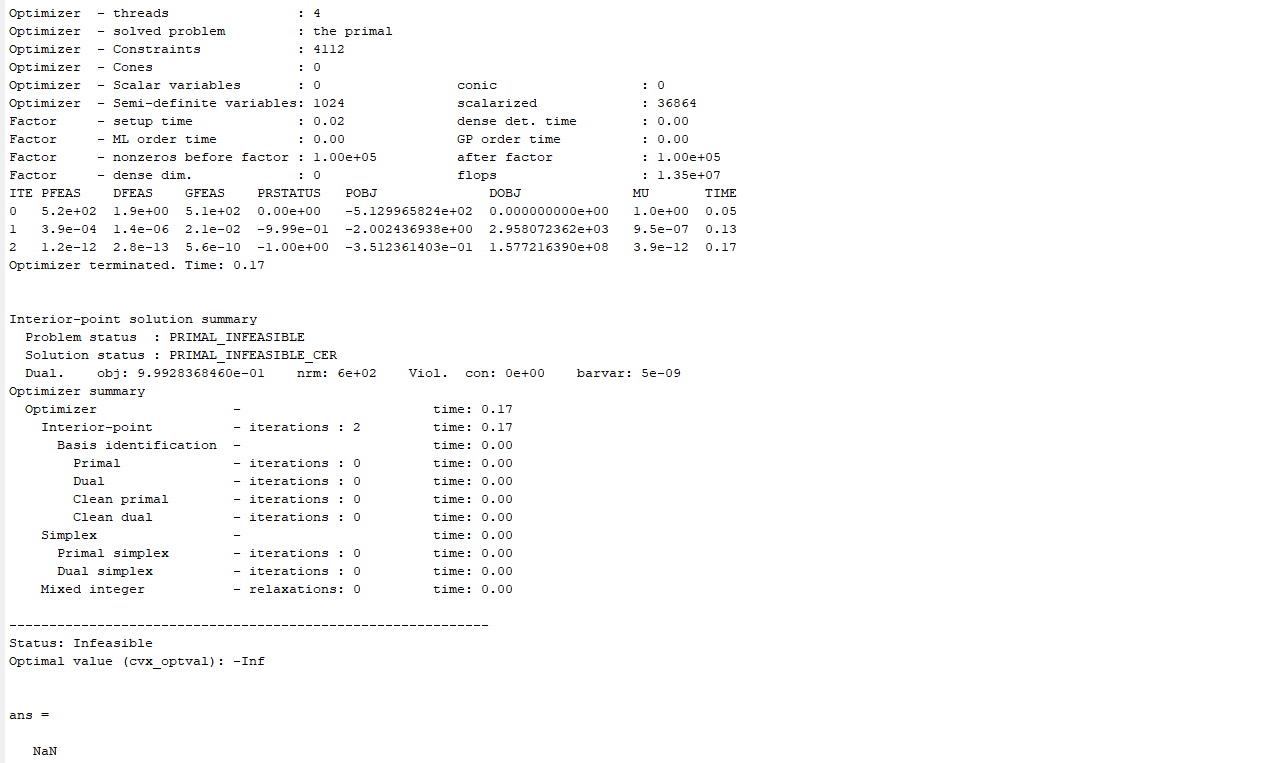
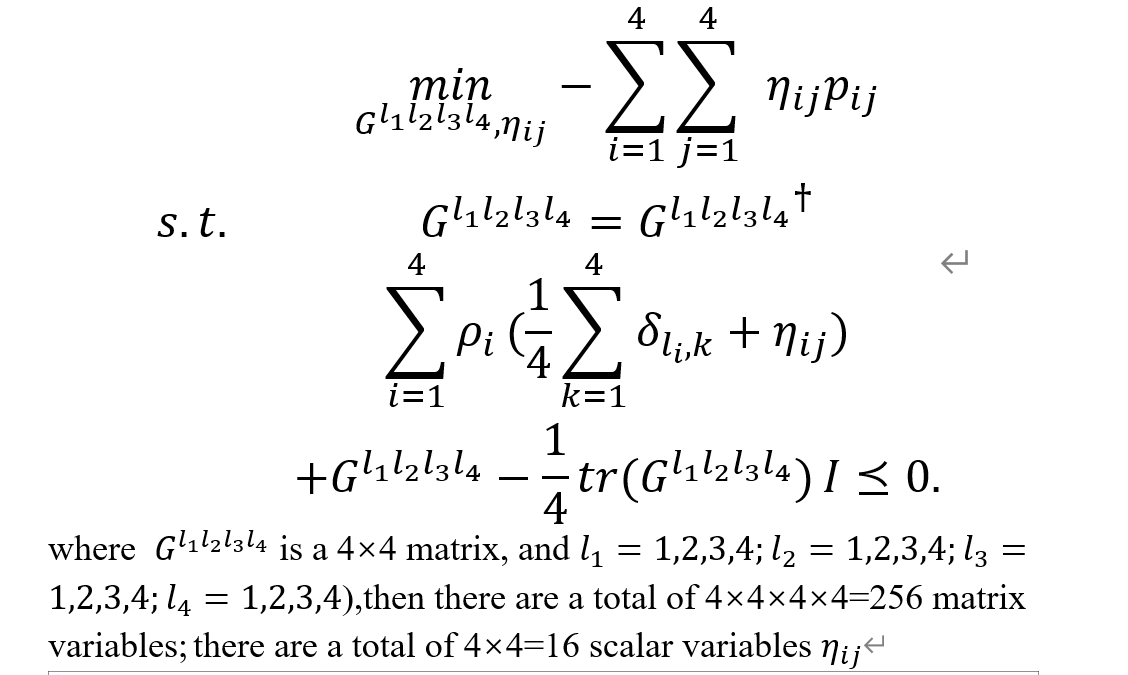Why is the solution state of my SDP model unbounded?But theoretically my SDP model should be bounded.
ph=0.05;eff=1;
lap=1-2*ph;
e0=[1;0;0;0];e1=[0;1;0;0];e2=[0;0;1;0];e3=[0;0;0;1];
p0=e0*e0';
p1=(lap*e0+sqrt(1-lap^2)*e1)*(lap*e0+sqrt(1-lap^2)*e1)';
p2=(lap*e0+lap*sqrt((1-lap)/(1+lap))*e1+sqrt((1+lap-2*lap^2)/(1+lap))*e2)*(lap*e0+lap*sqrt((1-lap)/(1+lap))*e1+sqrt((1+lap-2*lap^2)/(1+lap))*e2)';
p3=(lap*e0+lap*sqrt((1-lap)/(1+lap))*e1+lap*sqrt((1-lap)/(1+lap*(2*lap+1)))*e2+sqrt((-3*lap^2+2*lap+1)/(2*lap+1))*e3)*(lap*e0+lap*sqrt((1-lap)/(1+lap))*e1+lap*sqrt((1-lap)/(1+lap*(2*lap+1)))*e2+sqrt((-3*lap^2+2*lap+1)/(2*lap+1))*e3)';
u=[1 0 0 0;0 1 0 0;0 0 1 0;0 0 0 1];
pr=[0.312042591483681 ,0.187957408512046,0.187957408512046,0.312042591483681;
0.312042591483681,0.312042591483681,0.187957408512046,0.187957408512046;
0.187957408512046,0.312042591483681,0.312042591483681,0.187957408512046;
0.187957408512046,0.187957408512046,0.312042591483681,0.312042591483681];
cvx_solver mosek
cvx_begin
variable H(4,4,4,4,4,4) hermitian;
variable v(4,4);
y=-sum(sum(v.*pr));
minimize y
subject to
for u4=1:4
for u3=1:4
for u2=1:4
for u1=1:4
for j=1:4
-(p0*(1/4*kr(u1,j)+v(1,j))+p1*(1/4*kr(u2,j)+v(2,j))+p2*(1/4*kr(u3,j)+v(3,j))+p3*(1/4*kr(u4,j)+v(4,j))+H(:,:,u1,u2,u3,u4)-1/4*trace(H(:,:,u1,u2,u3,u4))*u)==semidefinite(4);
end
end
end
end
end
cvx_end