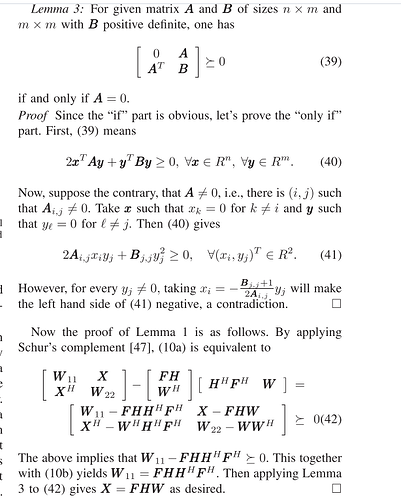Hi, wish to ask you something.
I’ve converted the equation constraint of X=B*W into the form of LMI as follows
\begin{bmatrix}
U & X & B \\
X^H & V & W^H \\
B^H & W & I_M
\end{bmatrix} \succeq 0
Tr(U) - M \leq 0 where U \in C^{MN*MN} and V \in C^{K*K} and U \succeq 0,V \succeq 0
The above equivalent forms of proof are as follows
Replace the FH in the image with B to get the result
But when I use LMI as a constraint in cvx, the X I got is not equal to B*W, why is that?
here is my code
numM=4;
numN=16;
numK=4;
gamak = 10^(4/10);
sigmak = 1.0e-4;
Hhat = [-0.0652405201837634 + 1.67262729732120i,-1.17955547159453 + 1.18751713760266i,-1.67191760052190 + 0.0764800249883790i,-1.28286695049747 - 1.07471836870477i,-0.482353009345158 + 1.60281755490566i,-1.43947387936296 + 0.853939918776870i,-1.63764897082401 - 0.344984216936885i,-0.972516792257723 - 1.36188439697510i,-0.868638242346595 + 1.43070133945419i,-1.60748313133005 + 0.465882848453379i,-1.49884726659665 - 0.744389533521191i,-0.600115527527786 - 1.56209162760993i,-1.19944121666771 + 1.16727447733334i,-1.67286688213672 + 0.0481216424873483i,-1.26438193493919 - 1.09624263443367i,-0.189440188150751 - 1.66256796317943i,-0.0652405201837634 + 1.67262729732120i,-1.17955547159453 + 1.18751713760266i,-1.67191760052190 + 0.0764800249883790i,-1.28286695049747 - 1.07471836870477i,-0.482353009345158 + 1.60281755490566i,-1.43947387936296 + 0.853939918776870i,-1.63764897082401 - 0.344984216936885i,-0.972516792257723 - 1.36188439697510i,-0.868638242346595 + 1.43070133945419i,-1.60748313133005 + 0.465882848453379i,-1.49884726659665 - 0.744389533521191i,-0.600115527527786 - 1.56209162760993i,-1.19944121666771 + 1.16727447733334i,-1.67286688213672 + 0.0481216424873483i,-1.26438193493919 - 1.09624263443367i,-0.189440188150751 - 1.66256796317943i,-0.0652405201837634 + 1.67262729732120i,-1.17955547159453 + 1.18751713760266i,-1.67191760052190 + 0.0764800249883790i,-1.28286695049747 - 1.07471836870477i,-0.482353009345158 + 1.60281755490566i,-1.43947387936296 + 0.853939918776870i,-1.63764897082401 - 0.344984216936885i,-0.972516792257723 - 1.36188439697510i,-0.868638242346595 + 1.43070133945419i,-1.60748313133005 + 0.465882848453379i,-1.49884726659665 - 0.744389533521191i,-0.600115527527786 - 1.56209162760993i,-1.19944121666771 + 1.16727447733334i,-1.67286688213672 + 0.0481216424873483i,-1.26438193493919 - 1.09624263443367i,-0.189440188150751 - 1.66256796317943i,-0.0652405201837634 + 1.67262729732120i,-1.17955547159453 + 1.18751713760266i,-1.67191760052190 + 0.0764800249883790i,-1.28286695049747 - 1.07471836870477i,-0.482353009345158 + 1.60281755490566i,-1.43947387936296 + 0.853939918776870i,-1.63764897082401 - 0.344984216936885i,-0.972516792257723 - 1.36188439697510i,-0.868638242346595 + 1.43070133945419i,-1.60748313133005 + 0.465882848453379i,-1.49884726659665 - 0.744389533521191i,-0.600115527527786 - 1.56209162760993i,-1.19944121666771 + 1.16727447733334i,-1.67286688213672 + 0.0481216424873483i,-1.26438193493919 - 1.09624263443367i,-0.189440188150751 - 1.66256796317943i;-0.343804065086222 + 1.25035870569987i,-1.06795829625980 + 0.735246840784658i,-1.29035582664988 - 0.125018060481049i,-0.906692521323401 - 0.926326781420968i,-1.07896619404889 + 0.719611186651815i,-1.28871167484363 - 0.144066446052317i,-0.893172045483233 - 0.939841133857426i,-0.0782781711894032 - 1.29400736073525i,-1.28678633003226 - 0.163093533043658i,-0.879450156536759 - 0.953158170652693i,-0.0592073577237805 - 1.29536180483867i,0.788609540458150 - 1.02911975684605i,-0.865529733721704 - 0.966274890298573i,-0.0401136141564769 - 1.29643518946567i,0.803908041314568 - 1.01764910784814i,1.27014673574948 - 0.261016824009327i,-0.343804065086222 + 1.25035870569987i,-1.06795829625980 + 0.735246840784658i,-1.29035582664988 - 0.125018060481049i,-0.906692521323401 - 0.926326781420968i,-1.07896619404889 + 0.719611186651815i,-1.28871167484363 - 0.144066446052317i,-0.893172045483233 - 0.939841133857426i,-0.0782781711894032 - 1.29400736073525i,-1.28678633003226 - 0.163093533043658i,-0.879450156536759 - 0.953158170652693i,-0.0592073577237805 - 1.29536180483867i,0.788609540458150 - 1.02911975684605i,-0.865529733721704 - 0.966274890298573i,-0.0401136141564769 - 1.29643518946567i,0.803908041314568 - 1.01764910784814i,1.27014673574948 - 0.261016824009327i,-0.343804065086222 + 1.25035870569987i,-1.06795829625980 + 0.735246840784658i,-1.29035582664988 - 0.125018060481049i,-0.906692521323401 - 0.926326781420968i,-1.07896619404889 + 0.719611186651815i,-1.28871167484363 - 0.144066446052317i,-0.893172045483233 - 0.939841133857426i,-0.0782781711894032 - 1.29400736073525i,-1.28678633003226 - 0.163093533043658i,-0.879450156536759 - 0.953158170652693i,-0.0592073577237805 - 1.29536180483867i,0.788609540458150 - 1.02911975684605i,-0.865529733721704 - 0.966274890298573i,-0.0401136141564769 - 1.29643518946567i,0.803908041314568 - 1.01764910784814i,1.27014673574948 - 0.261016824009327i,-0.343804065086222 + 1.25035870569987i,-1.06795829625980 + 0.735246840784658i,-1.29035582664988 - 0.125018060481049i,-0.906692521323401 - 0.926326781420968i,-1.07896619404889 + 0.719611186651815i,-1.28871167484363 - 0.144066446052317i,-0.893172045483233 - 0.939841133857426i,-0.0782781711894032 - 1.29400736073525i,-1.28678633003226 - 0.163093533043658i,-0.879450156536759 - 0.953158170652693i,-0.0592073577237805 - 1.29536180483867i,0.788609540458150 - 1.02911975684605i,-0.865529733721704 - 0.966274890298573i,-0.0401136141564769 - 1.29643518946567i,0.803908041314568 - 1.01764910784814i,1.27014673574948 - 0.261016824009327i;1.24071728293608 + 0.179700700227814i,0.565630468269524 + 1.11880312846160i,-0.590860743445215 + 1.10568006280365i,-1.24445830743253 + 0.151508734102732i,1.09904450999016 + 0.603062835730714i,0.137709106594817 + 1.24603626150278i,-0.940822794842869 + 0.828498146916922i,-1.21860772769445 - 0.294174213602628i,0.818007754776487 + 0.949925700276277i,-0.307651423969747 + 1.21525004163040i,-1.17145771003041 + 0.446268348504055i,-1.03822464696225 - 0.702527390284345i,0.433253630806475 + 1.17630723947605i,-0.713973131056792 + 1.03035738120908i,-1.25352492371160 + 0.00746783946372853i,-0.726192444501054 - 1.02176884769965i,1.24071728293608 + 0.179700700227814i,0.565630468269524 + 1.11880312846160i,-0.590860743445215 + 1.10568006280365i,-1.24445830743253 + 0.151508734102732i,1.09904450999016 + 0.603062835730714i,0.137709106594817 + 1.24603626150278i,-0.940822794842869 + 0.828498146916922i,-1.21860772769445 - 0.294174213602628i,0.818007754776487 + 0.949925700276277i,-0.307651423969747 + 1.21525004163040i,-1.17145771003041 + 0.446268348504055i,-1.03822464696225 - 0.702527390284345i,0.433253630806475 + 1.17630723947605i,-0.713973131056792 + 1.03035738120908i,-1.25352492371160 + 0.00746783946372853i,-0.726192444501054 - 1.02176884769965i,1.24071728293608 + 0.179700700227814i,0.565630468269524 + 1.11880312846160i,-0.590860743445215 + 1.10568006280365i,-1.24445830743253 + 0.151508734102732i,1.09904450999016 + 0.603062835730714i,0.137709106594817 + 1.24603626150278i,-0.940822794842869 + 0.828498146916922i,-1.21860772769445 - 0.294174213602628i,0.818007754776487 + 0.949925700276277i,-0.307651423969747 + 1.21525004163040i,-1.17145771003041 + 0.446268348504055i,-1.03822464696225 - 0.702527390284345i,0.433253630806475 + 1.17630723947605i,-0.713973131056792 + 1.03035738120908i,-1.25352492371160 + 0.00746783946372853i,-0.726192444501054 - 1.02176884769965i,1.24071728293608 + 0.179700700227814i,0.565630468269524 + 1.11880312846160i,-0.590860743445215 + 1.10568006280365i,-1.24445830743253 + 0.151508734102732i,1.09904450999016 + 0.603062835730714i,0.137709106594817 + 1.24603626150278i,-0.940822794842869 + 0.828498146916922i,-1.21860772769445 - 0.294174213602628i,0.818007754776487 + 0.949925700276277i,-0.307651423969747 + 1.21525004163040i,-1.17145771003041 + 0.446268348504055i,-1.03822464696225 - 0.702527390284345i,0.433253630806475 + 1.17630723947605i,-0.713973131056792 + 1.03035738120908i,-1.25352492371160 + 0.00746783946372853i,-0.726192444501054 - 1.02176884769965i;0.744052980415410 + 0.422486488019040i,0.0782469583530654 + 0.852038966354416i,-0.654643750659819 + 0.550924552138733i,-0.826134857216619 - 0.222622584576821i,0.655475492798011 + 0.550391351049500i,-0.0773324313357631 + 0.852397663636049i,-0.743808051133347 + 0.423432385642987i,-0.772423670857399 - 0.368633143340257i,0.545169516184055 + 0.660180545205781i,-0.230454496282484 + 0.824573953154341i,-0.808437014207177 + 0.281858826121668i,-0.693139653731680 - 0.502549050586954i,0.416768220359671 + 0.748212602618902i,-0.376055042570886 + 0.769469806496849i,-0.846378199753204 + 0.130875705770559i,-0.590887855771216 - 0.619934978684891i,0.744052980415410 + 0.422486488019040i,0.0782469583530654 + 0.852038966354416i,-0.654643750659819 + 0.550924552138733i,-0.826134857216619 - 0.222622584576821i,0.655475492798011 + 0.550391351049500i,-0.0773324313357631 + 0.852397663636049i,-0.743808051133347 + 0.423432385642987i,-0.772423670857399 - 0.368633143340257i,0.545169516184055 + 0.660180545205781i,-0.230454496282484 + 0.824573953154341i,-0.808437014207177 + 0.281858826121668i,-0.693139653731680 - 0.502549050586954i,0.416768220359671 + 0.748212602618902i,-0.376055042570886 + 0.769469806496849i,-0.846378199753204 + 0.130875705770559i,-0.590887855771216 - 0.619934978684891i,0.744052980415410 + 0.422486488019040i,0.0782469583530654 + 0.852038966354416i,-0.654643750659819 + 0.550924552138733i,-0.826134857216619 - 0.222622584576821i,0.655475492798011 + 0.550391351049500i,-0.0773324313357631 + 0.852397663636049i,-0.743808051133347 + 0.423432385642987i,-0.772423670857399 - 0.368633143340257i,0.545169516184055 + 0.660180545205781i,-0.230454496282484 + 0.824573953154341i,-0.808437014207177 + 0.281858826121668i,-0.693139653731680 - 0.502549050586954i,0.416768220359671 + 0.748212602618902i,-0.376055042570886 + 0.769469806496849i,-0.846378199753204 + 0.130875705770559i,-0.590887855771216 - 0.619934978684891i,0.744052980415410 + 0.422486488019040i,0.0782469583530654 + 0.852038966354416i,-0.654643750659819 + 0.550924552138733i,-0.826134857216619 - 0.222622584576821i,0.655475492798011 + 0.550391351049500i,-0.0773324313357631 + 0.852397663636049i,-0.743808051133347 + 0.423432385642987i,-0.772423670857399 - 0.368633143340257i,0.545169516184055 + 0.660180545205781i,-0.230454496282484 + 0.824573953154341i,-0.808437014207177 + 0.281858826121668i,-0.693139653731680 - 0.502549050586954i,0.416768220359671 + 0.748212602618902i,-0.376055042570886 + 0.769469806496849i,-0.846378199753204 + 0.130875705770559i,-0.590887855771216 - 0.619934978684891i]
cvx_begin
variable W(numM, numK) complex
variable X(numM*numN, numK) complex
variable U(numM*numN, numM*numN) complex semidefinite
variable V(numK, numK) complex semidefinite
variable I(numM, numM)
variable genhaoxia(numK,numK-1) complex
variable cal(numK,1)
variable bigmatrix(numM*numN+numK+numM,numM*numN+numK+numM) complex semidefinite
dual variables d1 d2 d3 d4 d5 d6
minimize( sum(sum_square_abs(W))) % conj( x ) .* x square_abs( x )
subject to
%X == B*W;
d5:bigmatrix == [ U X B ;
X' V W';
B' W I];
d6:trace(U) - numM <=0 ;
I == eye(numM);
tem = conj(Hhat)*X;
for i=1:numK
imag(tem(i,i)) == 0;
end
for i=1:numK
cal(i) == tem(i,i);
end
for i=1:numK
genhaoxia(i,:) == real(tem(i,setdiff(1:numK,i))) + imag(tem(i,setdiff(1:numK,i)))*1i;
end
d1:norm([tem(1,:) sigmak]) - real(tem(1,1))*sqrt((1+1/gamak)) <= 0 ;
d2:norm([tem(2,:) sigmak]) - real(tem(2,2))*sqrt((1+1/gamak)) <= 0 ;
d3:norm([tem(3,:) sigmak]) - real(tem(3,3))*sqrt((1+1/gamak)) <= 0 ;
d4:norm([tem(4,:) sigmak]) - real(tem(4,4))*sqrt((1+1/gamak)) <= 0 ;
cvx_end