Why is the error reported {convex} .* {real affine}

1

The goal is the sum of each element in the matrix to the third power, and I put a non-negative constraint on the constraint, and the cubed of an unknown quantity is convex if the unknown quantity is greater than zero, so why is this still an error
image
image

2

Because you didn’t follow CVX’s rules.

Use pow_pos or pow_p, with p = 3.

1 Like
3

Thank you very much. Could you tell me how to write such a goal? I have tried many ways, but they are all wrong
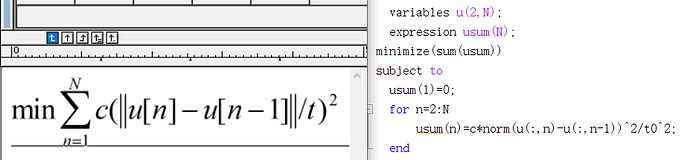
t and c are both constant，u is a variable of 2*1 dimensions
Thank you very much

image
image927×216 24.2 KB

4

You need to use square_pos when squaring norm.

1 Like
5

Thank you very much for your warm reply，I’ve got a new problem
This error occurs when I run the following code
错误使用 cvx/pow_cvx (line 144)
Disciplined convex programming error:
Illegal operation: pow_p( {convex}, {-1} )

for i=1:I
      for k=2:N
          sum21(k,i)=0;sum22(k,i)=0;
          for n=2:k
              G2=B*log2(1+Pi(n,i)*inv_pos(H^2+2*(u(:,n)-si(:,i))'*u(:,n)));
              sum21(k,i)= sum21(k,i)+tiulo(n,i)*G2;
              L2=t0*fiu(n,i)/ci(i);
              sum22(k,i)=sum22(k,i)+L2;
          end
          sum21(k,i)<=sum22(k,i);
      end
   end

image
image713×321 5.49 KB

There’s only one 2 N variable u, and the other parameters are known，G2=Blog2(1+Pi(n,i)inv_pos(H^2+2(u(:,n)-si(:,i))’*u(:,n))); is error
修改翻译结果

6

The argument of inv_pos needs to be concave. But it is not; hence the error.

Have you proven the optimization problem is convex?

7

I refer to a paper, which also uses CVX to solve a problem similar to mine, and proves that G2 is convex for u(n), but I don’t know why I made a mistake in writing the code

8

Please carefully read the link I provided.

9

Can I use rel_entr to solve such problem?

10

Not that i know of. But certainly not unless the problem is convex, whose determination i left in your hands. That said, I have no reason to believe this is a convex problem.

11

Well, thank you for taking the time to answer my childish questions