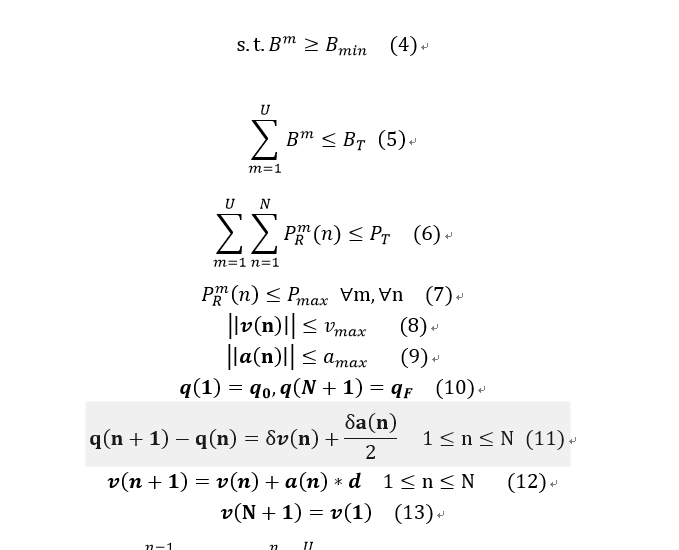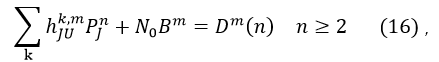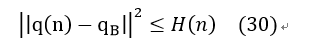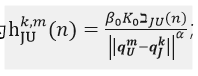Why does the solution contains NaN or inf while the cvx_status = 'Solved'

1

When i delete objective function to find a feasible point by cvx, the solution contains NaN or inf while the cvx_status = ‘Solved’ .I am puzzled to that wired solution.The following is my code in cvx：

cvx_begin
cvx_quiet true
cvx_solver sdpt3;
variable Q(3,N+1)
variable P(U,N+1) nonnegative
variable v(3,N+1) nonnegative
variable a(3,N+1) 
variable B(U,1) nonnegative
variable H(1,N) 
variable D(U,N+1) nonnegative
%%   feasible point 
subject to  
for n=1:N+1
    Q(3,n)==h;
end
for m=1:U
    B(m)>=1e6;
end
sum(B)<=B_T;

for m=1:U
    for n=2:N+1
        P(m,n)<=Pmax;
    end
end
sum(sum(P))<=P_T;

for n=1:N+1
    norm(v(:,n))<=vmax; %velocity constraint
    norm(a(:,n))<=amax; %acceleration constraint
end

Q(:,1)-[-550,100,100]' == 0;
[550,100,100]'-Q(:,N+1)  == 0;
v(:,N+1) == v(:,1);
for n=1:N
    Q(:,n+1)-Q(:,n) == d*v(:,n)+d*d*a(:,n)/2;
    v(:,n+1)==v(:,n)+a(:,n)*d;
end

expression sum_hJU(U,N+1)
for m=1:U
    for n=2:N+1
        sum_hJU(m,n)=0;
        for k=K+1:J
            sum_hJU(m,n)=sum_hJU(m,n)+h_JU(m,n,k);
        end
    D(m,n) == sum_hJU(m,n)*P_J+B(m)*N_0 ;   
    end
end
  
for n=1:N
    sum_square(Q(:,n)-Q_B(:))<=P_B*beta*H(n);
end
 
cvx_end
cvx_status
2

You haven;t provided a reproducible problem, complete with all input data.

You haven’t shown us the solver or CVX output. In order to see this output, do not use cvx_quiet true . You did not heed my advice from 3 months ago “I suggest you not use the quiet options until you are sure everything in your problem and its solution is working correctly and is understood.”

You haven’t shown us the “solution” (whatver you are referring to) containing NaN or inf.

With none of this information, let alone all of it, there is not much I can say.

3

1/
the problem is that i want to find some feasible points with cvx and the mathematical form of feasible problem is following :

图片
图片679×550 11.5 KB

图片
图片
图片
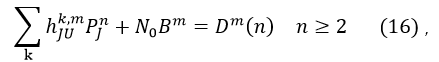
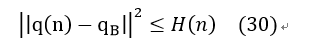
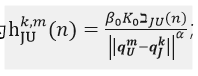
where the a and v is 3-dimension vector in each time slot and q is a 3-dimension vector whose third dimension is constant in each time slot.
2/
the input data is following:

U=2;
J=2;
K=1;
h=100;
N_0dbm=-170;
B_T=2*1e7;
Bmax=5*1e6;
N_0=power(10,N_0dbm/10)/1000;
B_0=2*1e7;
beta_dbm=-50;
beta=power(10,beta_dbm/10)/1000;
c=9.26*1e-4;
b=2250;
g=9.8;
vmax=40;
vmin=3;
amax=5;
d=1;
T=200;
N=T/d;
P_J=0.1;
P_B=0.1;
alpha=3;
K_0=10^-3;
ex=exprnd(1,N+1,1);
Pmax_dbm=16;
Pmax=power(10,Pmax_dbm/10)/1000;
Pave_dbm=10;
Pave=power(10,Pave_dbm/10)/1000;
P_T=N*Pave;
Q_0=[-550,100,100]';
Q_F=[550,100,100]';
Q_B=[-500,0,0]';
for k=1:K
    Q_J(:,k)=[-500+40*randn(1),50*randn(1),0]';
end
for k=K+1:J
    Q_J(:,k)=[300+30*randn(1),50+10*randn(1),0]';
end
for m=1:U
    Q_U(:,m)=[500+20*randn(1),100+20*randn(1),0]';
end
for m=1:U
    for n=1:N+1
        for k=K+1:J
            h_JU(m,n,k)=K_0*beta*ex(n)*power(norm(Q_U(:,m)-Q_J(:,k)),-alpha);
        end  
    end
end

3/
The CVX output is following :
Calling SDPT3 4.0: 5022 variables, 1608 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.

num. of constraints = 1608
dim. of socp var = 2608, num. of socp blk = 602
dim. of linear var = 2213
dim. of free var = 201
798 linear variables from unrestricted variable.
*** convert ublk to lblk
number of dense column in A = 1

SDPT3: Infeasible path-following algorithms

version predcorr gam expon scale_data
NT 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime

0|0.000|0.000|1.6e+03|4.3e+01|1.6e+12| 8.938271e+08 0.000000e+00| 0:0:00| spchol
SMW too ill-conditioned, switch to LU factor, Inf.
warning: symqmr failed: 0.3
switch to LU factor. splu 202 1
linsysolve: solution contains NaN or inf.
stop: difficulty in computing corrector directions

number of iterations = 1
primal objective value = 8.93827076e+08
dual objective value = 0.00000000e+00
gap := trace(XZ) = 1.62e+12
relative gap = 1.82e+03
actual relative gap = 1.00e+00
rel. primal infeas (scaled problem) = 1.61e+03
rel. dual " " " = 4.26e+01
rel. primal infeas (unscaled problem) = 0.00e+00
rel. dual " " " = 0.00e+00
norm(X), norm(y), norm(Z) = 2.0e+03, 0.0e+00, 8.1e+08
norm(A), norm(b), norm© = 8.2e+01, 1.0e+00, 1.9e+07
Total CPU time (secs) = 0.82
CPU time per iteration = 0.82
termination code = 0
DIMACS: 1.6e+03 0.0e+00 4.3e+01 0.0e+00 1.0e+00 1.8e+03

Status: Solved
Optimal value (cvx_optval): -8.93827e+08
4/

图片
图片1583×627 4.85 KB
this is the optimal result of B.
图片
图片1383×652 3.5 KB
this is the optimal result of P
Actually,they neither satisfy the constraint.

4

What evidence do you have that constraints are not satisfied? How much are they violated by? CVX and the solvers allow a solver feasibility tolerance, so that constraints might be violated by, for instance 1e-8 or less and still be considered to be satisfied.

Where is the NaN or Inf? Do not misinterpret linsysolve: solution contains NaN or inf, which is internal information from the solver, and does not pertain to the CVX solution.

Also, unlike CVX variables, CVX expressions might not be at their “optimal” (solution) value after CVX exits. The only way to check whether constraints involving CVX expressions are satisfied is to compute the value of the CVX expressions, starting from the values of CVX variables.

5

For example,As you see,B should be greater than 1e6 however my result not satisfies the consraint.

6

Apparently SDPT3 is getting screwed up by the horrible input data (scaling) in your problem (very large and small magnitude non-zero numbers). It appears that SDPT3 is at fault (a bug) for reporting termination code 0, even though optimality wasn’t achieved. CVX then reports Solved, based on the incorrect termination code reported by SDPT3.

SeDuMi fails, resulting in CVX reporting Failed.

Mosek issues warnings about near-zero elements, but claims to, and does appear to correctly find a feasible, hence optimal, solution, and CVX reports Solved.

7

I know my input data maybe unreasonable.You mean I need to change my data.Except for changing data ,whether the writing in cvx form is incorrect

8

I haven’t checked whether your code is correct, but the input data is horrible. Very small non-zero numbers are bad. Numbers such as 1e6 are bad. If you use such numbers, you are asking for trouble.

Mosek is a numerically more robust solver than SeDuMi or SDPT3, so you can get away with more bad stuff. But it is better to improve the input data (change variable scaling (units) or something).

9

Right,I understand .Thank you for your reply

10

Sorry,but maybe i will trouble you again.In fact i change the data to a small scalar the problem still exists while delete the equality constraint the problem disappears .I wonder wheather i write the equality constraint incorrectly in CVX. The equality constraint i mean:Q(:,1)-[-550,100,100]’ == 0;
[550,100,100]’-Q(:,N+1) == 0;
v(:,N+1) == v(:,1);
for n=1:N
Q(:,n+1)-Q(:,n) == d*v(:,n)+(d^2)*a(:,n)/2;
v(:,n+1)==v(:,n)+a(:,n)*d;
end
and the Mathematical form is following:
q(0)=q_0,q(N+1)=q_F (10)
q(n+1)-q(n)=δv (n)+(δa (n))/2 (11)
v (n+1)=v (n)+a (n)*d n≥0 (12)
v (N+1)=v (0) (13)

11

What problem still persists? What is your input data now? Constraining variables to be >= 1e6 is not a good thing to do numerically.