Why do variables that have been constrained greater than or equal to 0 have negative values？

1

for o=1:10
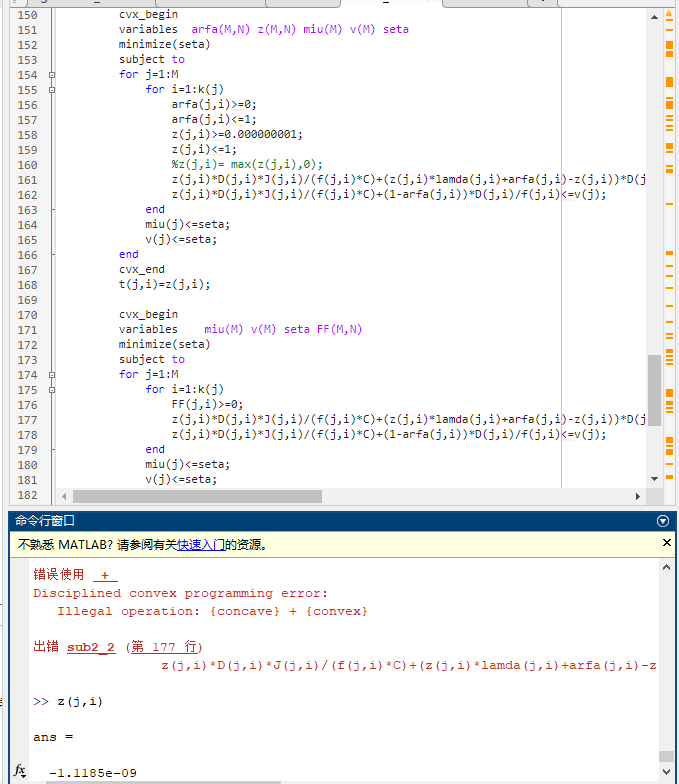
cvx_begin
variables arfa(M,N) z(M,N) miu(M) v(M) seta
minimize(seta)
subject to
for j=1:M
for i=1:k(j)
arfa(j,i)>=0;
arfa(j,i)<=1;
z(j,i)>=0;
z(j,i)<=1;
z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(z(j,i)*lamda(j,i)+arfa(j,i)-z(j,i))D(j,i)/(CR(j,i))+z(j,i)*lamda(j,i)*D(j,i)*K(j)/(F(j,i)*C)+(1-arfa(j,i))*D(j,i)/F(j,i)<=miu(j);
z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(1-arfa(j,i))*D(j,i)/f(j,i)<=v(j);
end
miu(j)<=seta;
v(j)<=seta;
end
cvx_end
t(j,i)=z(j,i);

    cvx_begin
    variables    miu(M) v(M) seta FF(M,N)
    minimize(seta)
    subject to
    for j=1:M
        for i=1:k(j)
            FF(j,i)>=0;
            z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(z(j,i)*lamda(j,i)+arfa(j,i)-z(j,i))*D(j,i)/(C*R(j,i))+inv_pos(FF(j,i))*z(j,i)*lamda(j,i)*D(j,i)*K(j)/C+(1-arfa(j,i))*D(j,i)*inv_pos(FF(j,i))<=miu(j);
            z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(1-arfa(j,i))*D(j,i)/f(j,i)<=v(j);
        end
        miu(j)<=seta;
        v(j)<=seta;
        t=sum(FF');
        t(j)<=Fm(j);
    end
    cvx_end
    F=FF;
    aa=seta;
end

Above is my code

Disciplined convex programming error:
Illegal operation: {concave} + {convex}

出错 sub2_2 (第 176 行)
z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(z(j,i)*lamda(j,i)+arfa(j,i)-z(j,i))D(j,i)/(CR(j,i))+inv_pos(FF(j,i))*z(j,i)*lamda(j,i)*D(j,i)*K(j)/C+(1-arfa(j,i))*D(j,i)*inv_pos(FF(j,i))<=miu(j);

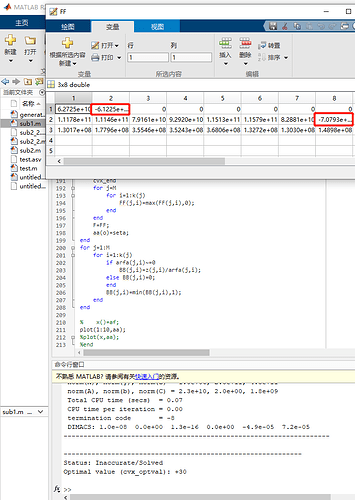
in the sub1，the solution value of z is negative.

2

image

3

With regards to z taking negative values, you can add the constraint z>=1e-6 and check if that solves the problem. Kindly check this answer by @Mark_L_Stone here How do I limit the optimization variable to be non-negative when I'm using the sedumi solver.

4

Thank you very much for your suggestion, but there will still be negative numbers

5

Please show us the complete “still be” problem, with all solver and CVX output, and the evidence of negative numbers in violation of constraints. Did you change the constraint from z(j,i) >= 0 to z(j,i) >= 1e-6?

Use of for constraints to set variable bounds in not incorrect, but it is inefficient in CVX processing time.

Outside of for loops, you can use

1e-6 <= z <= 1
0 <= arfa <= 1
miu <= seta
v <= seta

These impose bound constraints on every element of the arrays. The only time you can’t do it this way is if using sdp mode when the array (matrix) is square, in which case CVX would interpret the inequality constraint as an SDP constraint, rather than element-wise inequality constraints. Even in SDP mode, you could still use 0 <= arfa(:) <= 1, which imposes element-wise bound constraints on every element of the vector arfa(:).

6

image
image679×784 27.3 KB

this is the "still is"s evidence.At line 158， I have set the range of z.
Because I used the BCD algorithm, in the first problem, I got z, but some z is negative, so, in the second problem, there is a convex and concave error.
Thanks for your reply.

7

My post which @Sly-ney linked suggested 1e-5 or 1e-6, and @Sly-ney specifically suggested 1e-6, for lower bound in place of zero. You used 1e-9, which is tool small a number to ensure the solver will return a nonnegative number. Please try again, but this time use 1e-5 or 1e-6. as lower bound for z

8

In addition to that, z=max(z,0) should be used after the line “cvx_end” and not before as you have in line 160.

I must add you should try @Mark_L_Stone suggestion to use 1e-6 first. If that still doesnt work, then try the z=max(z,0). Also, can you please mention if you do get any warnings on large numerical values?

9

Thank you so much. I’ve solved my first problem.But the same case happened in the next problem.

for o=1:10
    cvx_begin
    variables  arfa(M,N) z(M,N) miu(M) v(M) seta
    minimize(seta)
    subject to
    for j=1:M
        for i=1:k(j)
            arfa(j,i)>=0;
            arfa(j,i)<=1;
            arfa(j,i)>=z(j,i);
            z(j,i)>=1e-6;
            z(j,i)<=1;
            %z(j,i)= max(z(j,i),0);
            z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(z(j,i)*lamda(j,i)+arfa(j,i)-z(j,i))*D(j,i)/(C*R(j,i))+z(j,i)*lamda(j,i)*D(j,i)*K(j)/(F(j,i)*C)+(1-arfa(j,i))*D(j,i)/F(j,i)<=miu(j);
            z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(1-arfa(j,i))*D(j,i)/f(j,i)<=v(j);
        end
        miu(j)<=seta;
        v(j)<=seta;
    end
    cvx_end
    for j=1:M
        for i=1:k(j)
            arfa(j,i)=max(arfa(j,i),0);
        end
    end
    cvx_begin
    variables    miu(M) v(M) seta FF(M,N)
    minimize(seta)
    subject to
    for j=1:M
        for i=1:k(j)
            FF(j,i)>=1e-6;
            z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(z(j,i)*lamda(j,i)+arfa(j,i)-z(j,i))*D(j,i)/(C*R(j,i))+inv_pos(FF(j,i))*z(j,i)*lamda(j,i)*D(j,i)*K(j)/C+(1-arfa(j,i))*D(j,i)*inv_pos(FF(j,i))<=miu(j);
            z(j,i)*D(j,i)*J(j,i)/(f(j,i)*C)+(1-arfa(j,i))*D(j,i)/f(j,i)<=v(j);
        end
        miu(j)<=seta;
        v(j)<=seta;
        t=sum(FF');
        t(j)<=Fm(j);
    end
    cvx_end
    for j=M
        for i=1:k(j)
            FF(j,i)=max(FF(j,i),0);
        end
    end
    F=FF;
    aa(o)=seta;
end
for j=1:M
    for i=1:k(j)
        if arfa(j,i)~=0
            BB(j,i)=z(j,i)/arfa(j,i);
        else BB(j,i)=0;
        end
        BB(j,i)=min(BB(j,i),1);
    end
end

in the sub2,I’ve I have asked FF（j，i）>=1e-6,To ensure that FF is greater than or equal to 0, I added FF(j,i)=max(FF(j,i),0) after cvxend.But FF will still have a negative number.

Here is my evidence.

image
image715×1006 50.8 KB

10

I don 't know what you’ve done if you used max(double precision scalar,0) after cvx_end, and that is still negative. At that point, that has nothing to do with CVX, it is “pure” MATLAB" double precision. Instead of posting images, you show show everything copying and pasting commands and all output, which should include displaying the supposedly negative variables.

As for the possibility of 1e-6 not preventing a negative number, CVX status is Inaccurate/Solved, and the solver norms displayed are huge, which means that 1e-6 might be quite small in comparison top those huge numbers, and the solution itself sloppy based on Inaccurate’/Solved.

How did this happen? it could happen from very large input data in your original problem. But even it that data were not huge, once you start using the output of one CVX problem as input for the next in an unsafeguarded SCA algorithm, things can explode over one or more iterations to produce wilder and wilder problem inputs and solutions, until the solver eventually encounters numerical problems or incorrect infeasibility or unboundedness claims arising from the horribly scaled numbers.

https://twitter.com/themarklstone/status/1586795881168265216