Hi,
I want to simulate the LMI problem which exist in the article.
but it takes this error:
Error using reshape
To RESHAPE the number of elements must not change.
Error in cvx/cat (line 102)
yb = reshape( yb, nz, psz );
Error in cvx/horzcat (line 2)
y = cat( 2, varargin{:} );
clc
clear all
close all
A = [-0.45 0.45 0;0.09 0.225 -0.45;0.135 0.135 -0.54];
B = [1 0;0.2 1;0 .3];
C = [0.1 0.8 0.7;-0.6 0.9 0.6];
Ad = [-0.04 0.02 0;0.02 -0.16 0.04;0.2 -0.06 -0.2];
D1 =[0.1;0;0.2]
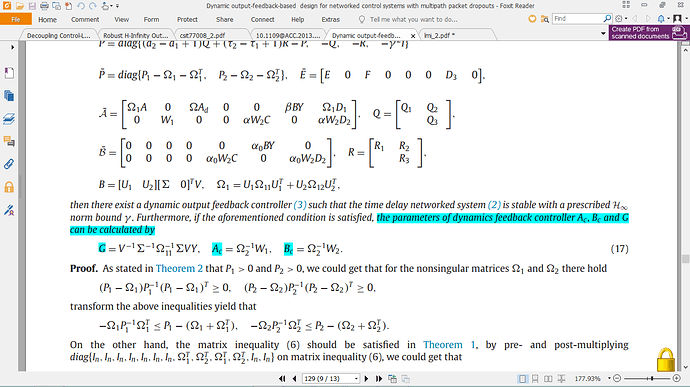
D2 =[1;0]
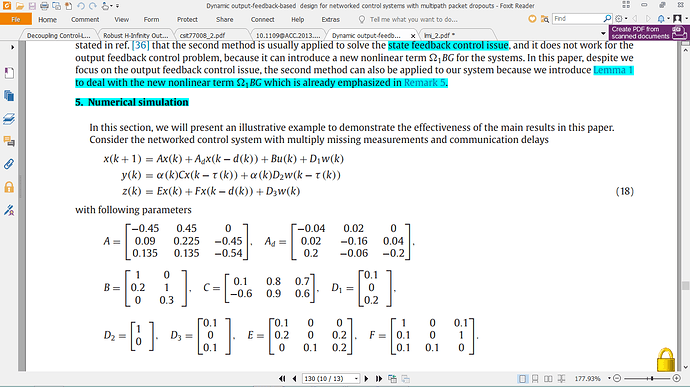
D3 =[0.1;0;0.1]
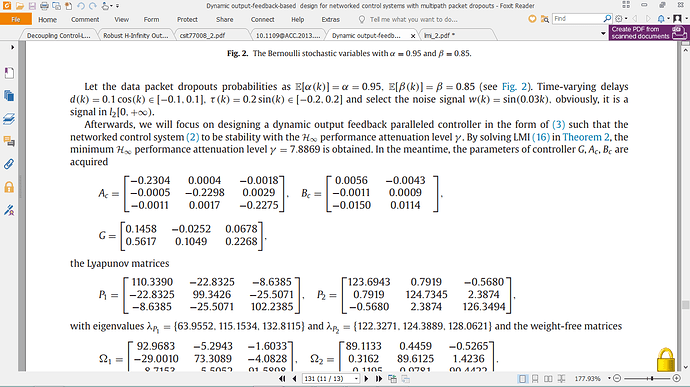
E =[0.1 0 0;0.2 0 0.2;0 0.1 0.2]
F =[1 0 0.1;0.1 0 1;0.1 0.1 0]
n = size(A,1);
[n,m] = size(B);
[q,n] = size©;
d1=-0.1;d2=0.1;
T1=-0.2;T2=0.2;
alpha=0.95
beta=.85
alpha0 =sqrt(alpha*(1-alpha))
beta0 = sqrt(beta*(1-beta))
[U,S,V] = svd(B)
U1 =U(:,1:2)
U2 =U(:,3)
cvx_begin sdp
variable gama
variable omega11(m,m)
variable omega12(n-m,n-m)
variable omega21(m,m)
variable omega22(n-m,n-m)
variable W2(n,m)
variable Y(q,n)
variable W1(n,n)
omega1 = U1omega11U1’+U2omega12U2’
omega2 = U1omega21U1’+U2omega22U2’
omegaT1= inv(V)pinv(S)omega1SV
omegaT2 = inv(V)pinv(S)omega2SV
%decision variable
variable P1(n,n)
variable P2(n,n)
variable Q1(n,n)
variable Q2(n,n)
variable Q3(n,n)
variable R1(n,n)
variable R2(n,n)
variable R3(n,n)
Q = [Q1 Q2;Q2’ Q3]
R = [R1 R2;R2’ R3]
P =blkdiag(P1,P2)
Phat = blkdiag((d2-d1+1)*Q+(T2-T1+1)R-P,-Q,-R,-gama^2eye(6))
PTel = blkdiag(P1-omega1-omega1’,P2-omega2-omega2’)
Etel =[E zeros(n) F zeros(n) zeros(n) zeros(n) D3 zeros(n,5)]
Atel = [omega1A zeros(n) omega1Ad zeros(n,7) zeros(n) betaBY omega1D1 zeros(n,1);zeros(n) W1 zeros(n) zeros(n,7) alphaW2C zeros(n) zeros(n,1) alphaW2D2]
Btel = [zeros(n,5) zeros(n) zeros(n) zeros(n) zeros(n) alpha0BY zeros(n) zeros(n,1);zeros(n,5) zeros(n) zeros(n) zeros(n) alpha0W2C zeros(n) zeros(n) alpha0W2*D2]
minimize gama
subject to
[Phat Atel’ Btel’ Etel’;
Atel PTel zeros(6) zeros(6,3);
Btel zeros(6) PTel zeros(6,3);
Etel zeros(3,6) zeros(3,6) -eye(n)]<=0
cvx_end
G = inv(omegaT1)(Y)
Bc = inv(omega2)(W1)
Ac = inv(omega2)*(W2)