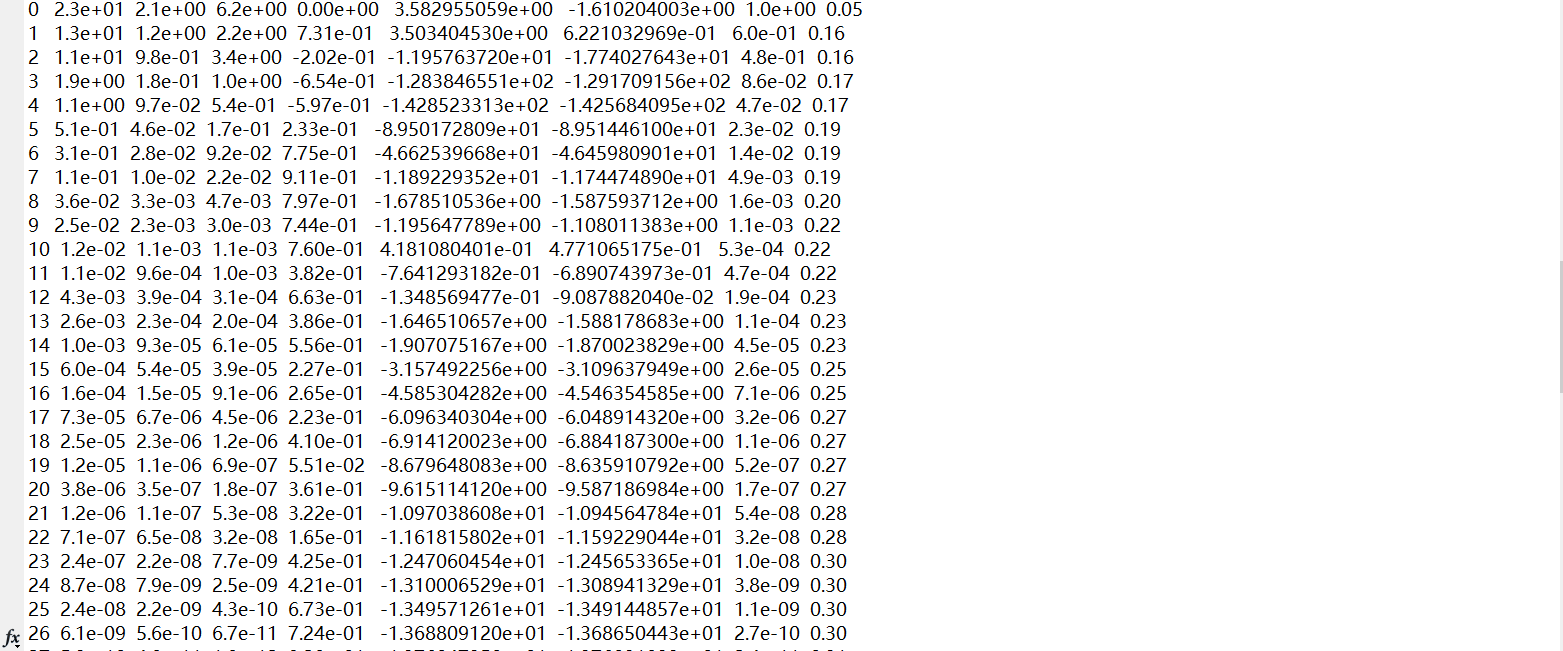
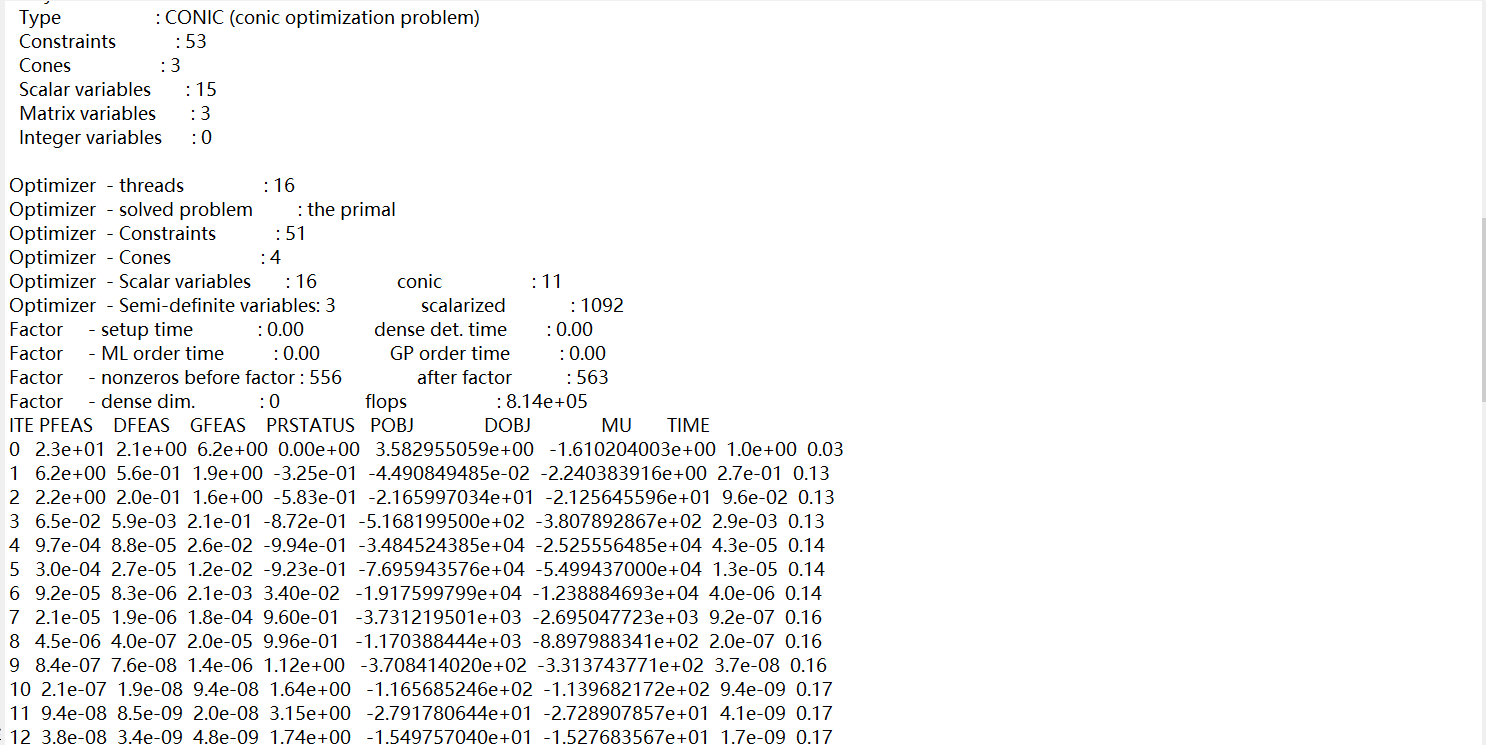
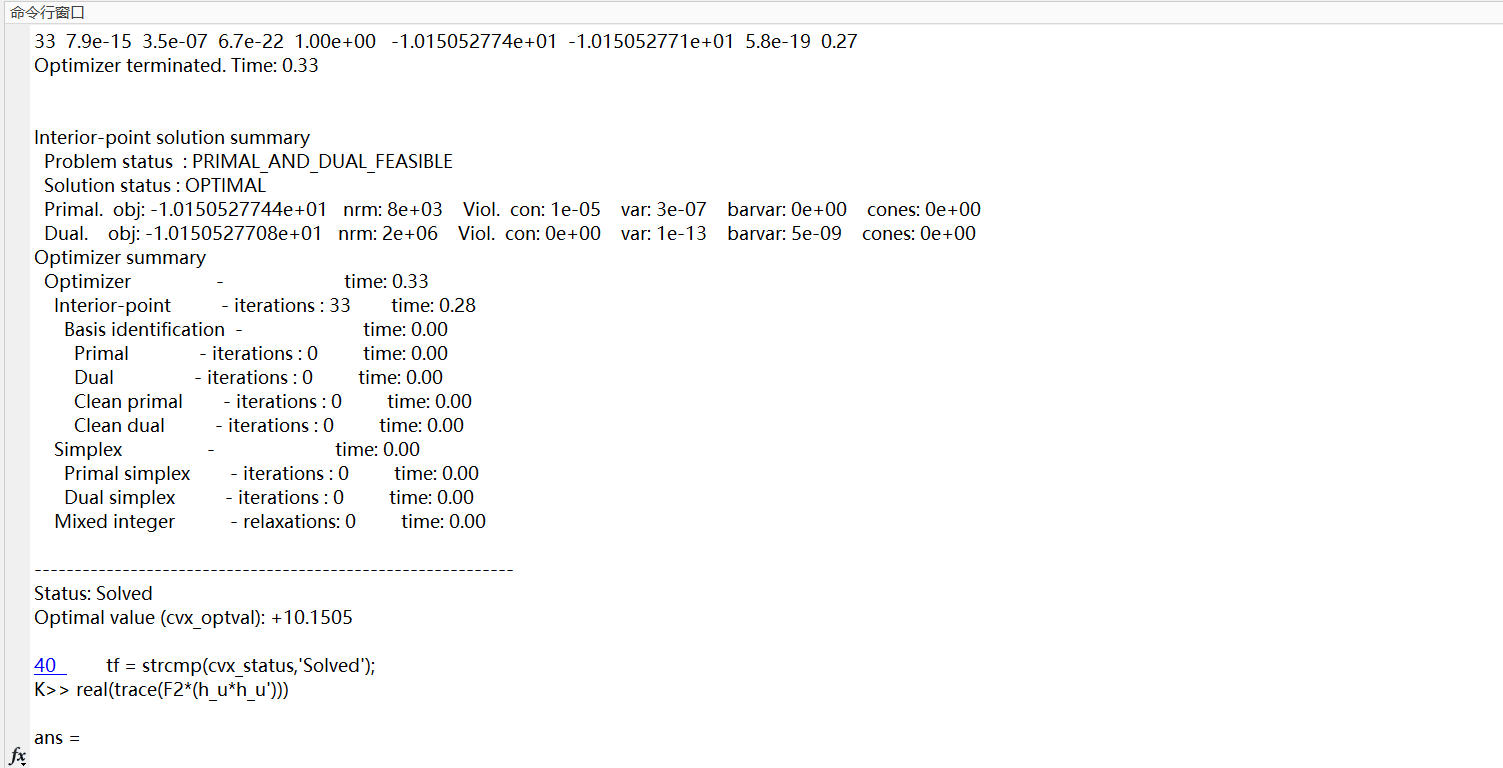
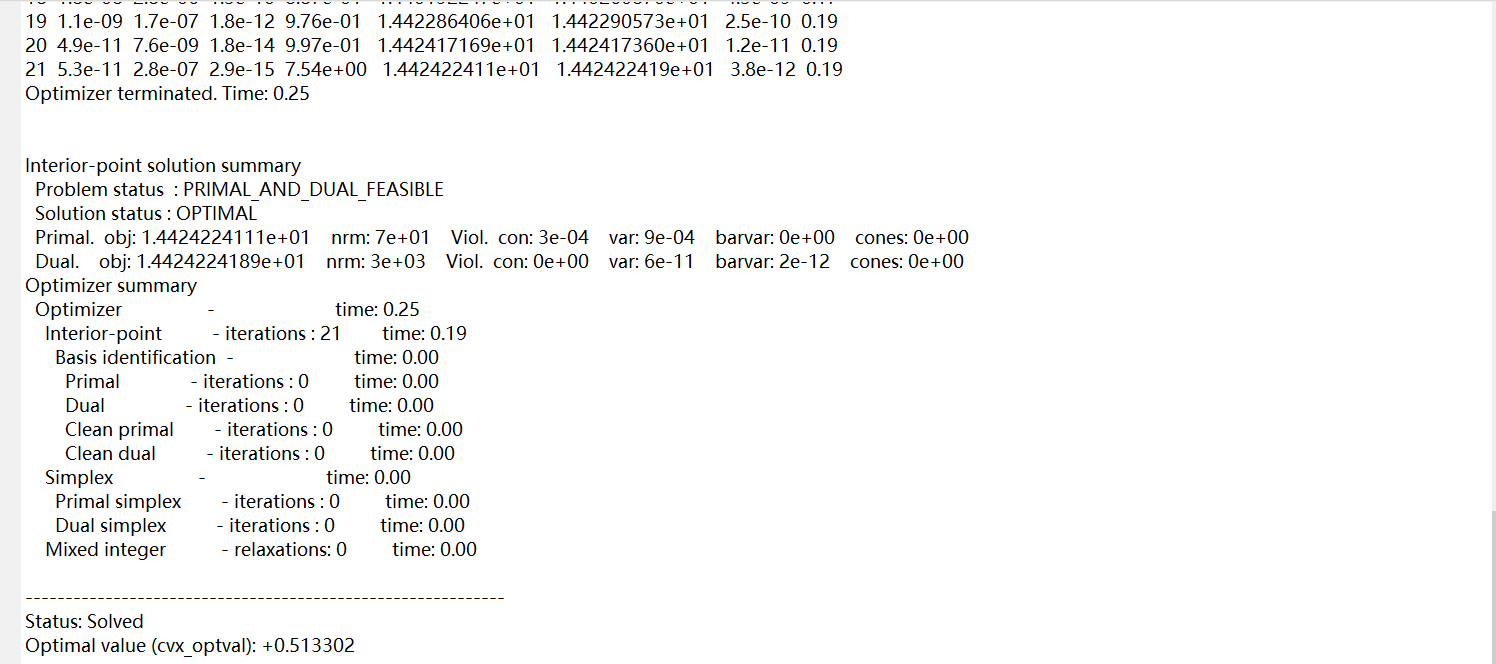
That could be attributed to small violations, the solution will never satisfy == . Remove “quiet” and see log output to see how it went.
The amount of violation reported by Mosek is comparable with the amount of violation reported by cvx. The dual solution has a huge norm and the optimization STATUS column fails to clearly converge which could indicate an illposed or borderline feasible problem. In any case some numerical issues you need to address in your data/model. Does not look like a cvx issue though.
This can help https://docs.mosek.com/latest/toolbox/debugging-log.html
ok,thank you very much
hello, i have changed my optimization problem,The norm of dual solution has decreased greatly, is this solution better and more feasible ?
cvx_solver mosek
cvx_save_prefs
factor = 1/Pmax;
F1_ini = f1_ini*f1_ini'*factor ;
F2_ini = f2_ini*f2_ini'*factor ;
Phi_ini = diag(v_ini);
h_u = (h_irs_u1_temp'*Phi_ini*H_bs_irs_temp)';
H_e = H_irs_e1_temp*Phi_ini*H_bs_irs_temp;
cvx_begin
variable F1(bs_antenna_number,bs_antenna_number) hermitian semidefinite
variable F2(bs_antenna_number,bs_antenna_number) hermitian semidefinite
variable q(4,1)
variable p(2,1) nonnegative
maximize (q(1)-q(2)-q(3)+q(4))
subject to
log(noise_power+real(trace((F1+F2)*(h_u*h_u')))/factor)>=q(1)*log(2)
A1 = noise_power+real(trace(F2_ini*(h_u*h_u')))/factor;
log(A1)+real(trace(h_u*h_u'*(F2-F2_ini)))/A1/factor<= q(2)*log(2)
A2 = H_e*(F1_ini+F2_ini)*H_e';
A2 = (A2+A2')/2/factor;
log_det(noise_power*eye(eve_antenna_number)+A2)...
+real(trace(H_e'*(noise_power*eye(eve_antenna_number)+A2)^(-1)*H_e*(F1-F1_ini)))/factor ...
+real(trace(H_e'*(noise_power*eye(eve_antenna_number)+A2)^(-1)*H_e*(F2-F2_ini)))/factor <=q(3)*log(2)
log_det(noise_power*eye(eve_antenna_number)+H_e*F2*H_e'/factor)>=q(4)*log(2)
q(1) - q(2) >= rate__user_th
bs_antenna_number*real(diag(F1)) == p(1)*factor
bs_antenna_number*real(diag(F2)) == p(2)*factor
sum(p) <= Pmax
F1 == hermitian_semidefinite(bs_antenna_number)
F2 == hermitian_semidefinite(bs_antenna_number)
cvx_end
hello, i have changed my model and scale the optimization variables, but the equality constraint is not satisfied.
can you help me? thank you.
Consider
>> 1/2-1/3-1/6
ans =
2.7756e-17
If that is not == 0, then how could the result of a complicated computation in practice satisfy some floating-point equality exactly?
The violations you show are of order 1e-9. That is as good as it normally gets.
See https://docs.mosek.com/modeling-cookbook/practical.html#the-quality-of-a-solution
ok,i got it, thank you very much