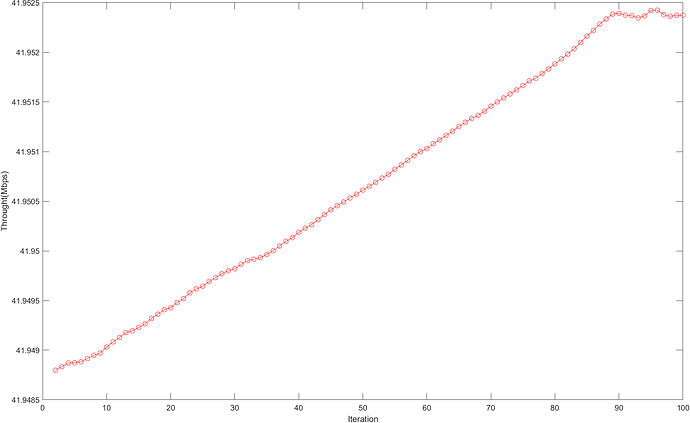
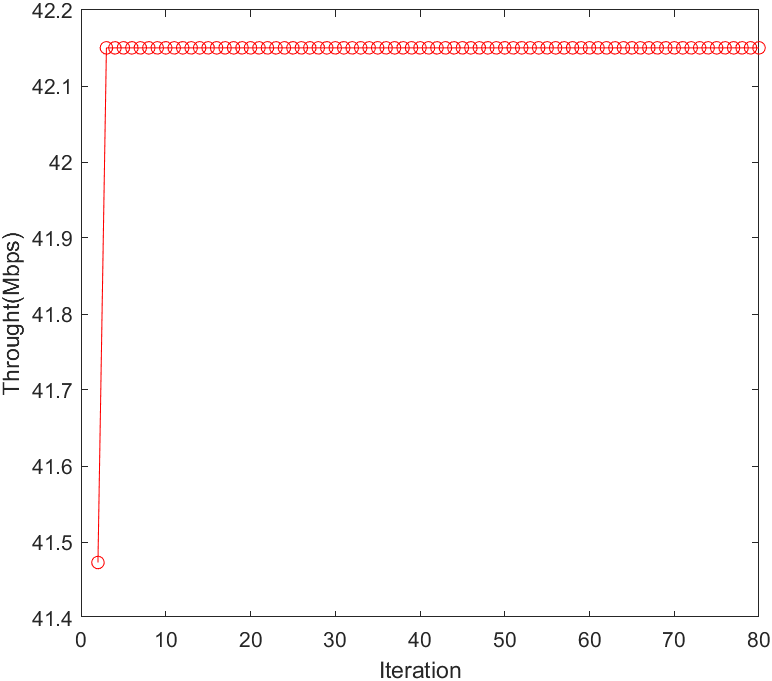
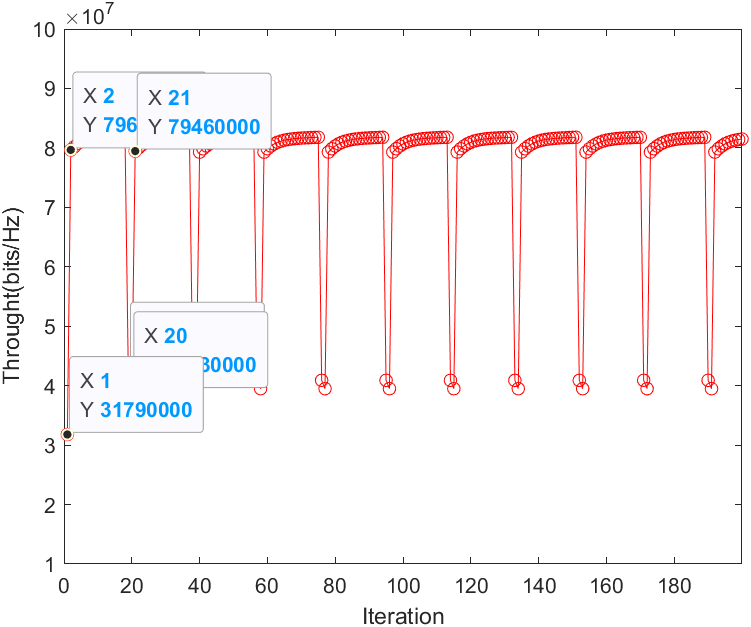
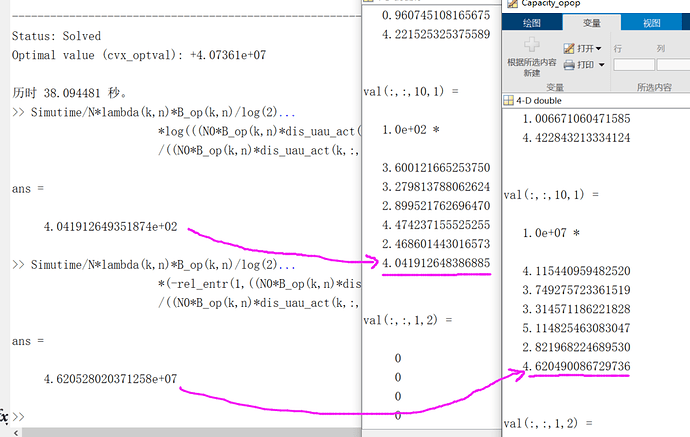
Hi there!
I am dealing with an optimization problem that I intend to solve it using the Block Coordinate Descent (BCD) method. Since I set the random initial value for variables when I run the code, the code doesn’t converge.
Primitive function like this f(x,y,z)=xzlog2(1+y/z)), I wonder if there is a CVX grammar writing problem or whether this function can not be solved by an iterative algorithm. I appreciate any help. Thank you in advance. Here is my code:
Iteration = 80;
P_op = randi([170,190],K,N);
B_op = randi([810^5,910^5],K,N);
c_op = 1;
lambda_op = zeros(K,N); % 0-1
for i = 2:Iteration
% ------Optimize x,that is,it is represent by lambda(K,N)----------------------------------
cvx_begin %quiet
%cvx_solver sedumi
variable lambda(K,N) nonnegative; %
expression B_width(1,K);
expression P_ower(1,K);
expression B_sum(1,N);
expression P_sum(1,N);
expression Capacity_op(K,1,N,Cir);
expression Capacity_op_th(1,K); %
expression Capacity_lambda(1,Iteration);
expression Capacity_op_total1(1,length(time_slot));
expression obj_1_1;
time_slot = 0:1:N;
for n = 1:(length(time_slot)-1)
for k = 1:K
Capacity_op(k,1,n,c_op) = Simutime/N*lambda(k,n)*B_op(k,n)/log(2)*log(1+(Beta0*P_op(k,n)/(N0 * B_op(k,n)*dis_uau_act(k,:,n,c_op)^2))); % the Capicity
B_width(k) = lambda(k,n)*B_op(k,n);
P_ower(k) = lambda(k,n)*P_op(k,n);
end
B_sum(n) = sum(B_width);
P_sum(n) = sum(P_ower);
end
for n = 1:(length(time_slot)-1)
Capacity_op_total1(n) = sum(Capacity_op(:,1,n,c_op)); % the capicity of every slots
end
for k = 1:K
Capacity_op_th(k) = sum(Capacity_op(k,1,:,c_op));
end
obj_1_1 = 1/Simutime*sum(Capacity_op_total1);
maximize(obj_1_1)
subject to
for n = 1:N
for k = 1:K
0 <= lambda(k,n) <= 1;
Capacity_op_th(k) >= 10^7;
end
B_sum(n) <= B_max;
P_sum(n) <= P_max;
end
cvx_end
lambda_op = roundn(lambda,-4);
% ------Optimize y, that is, it is represent by P_op1(K,N)----------------------------------
cvx_begin %quiet %
variable P_op1(K,N) nonnegative; %
expression P_ower1(1,K);
expression P_sum1(1,N);
expression Capacity_op2(K,1,N,Cir);
expression Capacity_op_th2(1,K);
expression Capacity_P(1,Iteration);
expression Capacity_op_total2(1,length(time_slot));
expression obj_1_2;
time_slot = 0:1:N;
for n = 1:(length(time_slot)-1)
for k = 1:K
Capacity_op2(k,1,n,c_op) = Simutime/N*lambda_op(k,n)*B_op(k,n)/log(2)*log(1+(Beta0*P_op1(k,n)/(N0*B_op(k,n)*dis_uau_act(k,:,n,c_op)^2)));
P_ower1(k) = lambda_op(k,n)*P_op1(k,n);
end
P_sum1(n) = sum(P_ower1);
end
for n = 1:(length(time_slot)-1)
Capacity_op_total2(n) = sum(Capacity_op2(:,1,n,c_op));
end
obj_1_2 = 1/Simutime*sum(Capacity_op_total2);
for k = 1:K
Capacity_op_th2(k) = sum(Capacity_op2(k,1,:,c_op));
end
maximize (obj_1_2)
subject to
for n = 1:N
for k = 1:K
0 <= P_op1(k,n) <= P_max;
Capacity_op_th2(k) >= 10^7;
end
P_sum1(n) <= P_max;
end
cvx_end
P_op = roundn(P_op1,-4);
% ------Optimize z, that is, it is represent by B_op1(K,N)----------------------------------
cvx_begin %quiet
variable B_op1(K,N) nonnegative; %
expression B_width1(1,K);
expression B_sum1(1,N);
expression Capacity_op3(K,1,N,Cir);
expression Capacity_op_th3(1,K);
expression Capacity_B(1,Iteration);
expression Capacity_op_total3(1,length(time_slot));
expression obj_1_3;
time_slot = 0:1:N;
for n = 1:(length(time_slot)-1)
for k = 1:K
% rel_entr
Capacity_op3(k,1,n,c_op) = Simutime/N*lambda_op(k,n)/log(2)...
*(-rel_entr(B_op1(k,n),B_op1(k,n)+(Beta0*P_op(k,n)/(N0*dis_uau_act(k,:,n,c_op)^2))));
B_width1(k) = lambda_op(k,n)*B_op1(k,n);
end
B_sum1(n) = sum(B_width1);
end
for n = 1:(length(time_slot)-1)
Capacity_op_total3(n) = sum(Capacity_op3(:,1,n,c_op));
end
Capacity_B(i) = 1/Simutime*sum(Capacity_op_total3);
obj_1_3 = 1/Simutime*sum(Capacity_op_total3);
for k = 1:K
Capacity_op_th3(k) = sum(Capacity_op3(k,1,:,c_op));
end
maximize (obj_1_3)
subject to
for n = 1:N
for k = 1:K
0 < B_op1(k,n) <= B_max;
Capacity_op_th3(k) >= 10^7;
end
B_sum1(n)<= B_max;
end
cvx_end
B_op = roundn(B_op1,-4);
end