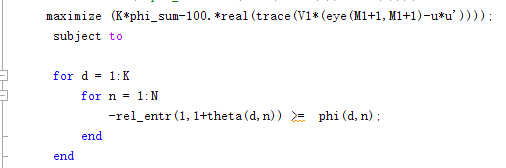
You show only a fragment of a program, don’t show any output, and we don’t even know what the question is.
Sorry,I post my complete code now.
function [P_out,Rate1,theta_out] = Phase_optimization(hb,hk,P_k)
%UNTITLED5 此处显示有关此函数的摘要
% 此处显示详细说明
M1 = 10; %RIS的数量
N = 12; %划分的时刻
K = 3; % 用户的数量
r = 1; %循环次数
N_max = 10;%最大循环次数
Omega = [0 0 0;0.5 0 0;0.5 0.5 0];
delta_noise = 0.001;
% Phase = 1*pi*ones(1,M);
Phase = 2*pi*rand(1,M1);
theta_phase = (exp(1i*Phase))';
V_ini=[theta_phase.',1].'*([theta_phase.',1].')';
theta_ini = 0.1*ones(K,N);
[eig_vec,eig_value]=eig(V_ini);
eig_max=max(max(eig_value));
[row,column]=find(eig_value==eig_max);
u = eig_vec(:,column);
hk1 = hk(1,:,:);%所有第一行的数据
hk2 = hk(2,:,:);%同上
hk3 = hk(3,:,:) ;
sum_rate = [];
sheet = [2 3;1 3;1 2];
Rkk = zeros(M1+1,(M1+1)*3);
a = zeros(M1,K,N);
G = hb;
for n = 1:N %k = 1
a(:,1,n)=diag(hk1(:,:,n))*G(:,1,n);%hk是一个M*M*N的矩阵,G是一个M*1*N的矩阵
end
for n = 1:N %k = 2
a(:,2,n)=diag(hk2(:,:,n))*G(:,1,n); %hk是一个M*M*N的矩阵,G是一个M*1*N的矩阵
end
for n = 1:N %k = 3
a(:,3,n)=diag(hk3(:,:,n))*G(:,1,n);%hk是一个M*M*N的矩阵,G是一个M*1*N的矩阵
end
%Rkk
for n = 1:N
Rkk(1:M1,1:M1,n) = a(:,1,n)*a(:,1,n)'; %k = 1
Rkk(1:M1,M1+2:M1+11,n) = a(:,2,n)*a(:,2,n)'; %k = 2
Rkk(1:M1,M1+13:M1+22,n) = a(:,3,n)*a(:,3,n)'; %k = 3
end
%Rkj
% for n = 1:N
% Rkj(1:M,1:M,n) = a(:,1,n)*a(:,1,n)'; %k = 1
% Rkj(1:M,M+2:M+11,n) = a(:,2,n)*a(:,2,n)'; %k = 2
% Rkj(1:M,M+13:M+22,n) = a(:,3,n)*a(:,3,n)'; %k = 3
% end
%middle = 1;
%accuracy = 1;
tic
while (r<=N_max)
cvx_begin
variable V1(M1+1,M1+1) complex semidefinite;
variable phi(K,N);
variable theta(K,N);
variable phi_sum;
% expression right(K)
% for i = 1 : K
% for j=1:K
% right(i)=right(i)+real(trace(R((N+1)*(j-1)+1:(N+1)*j,:,i)*V));
% end
% end
% maximize (K*phi_sum+100.*(real(trace(V1))-norm(V1)));
maximize (K*phi_sum-100.*real(trace(V1*(eye(M1+1,M1+1)-u*u'))));
subject to
% for d = 1:K
% for n = 1:N
% -rel_entr(1,1+theta(d,n)) >= phi(d,n);
% end
% end
for n = 1:N
for d = 1:K
phi(d,n) <= log(1+theta(d,n));
end
end
sum(phi,2) >= phi_sum;
% k = 1
for n = 1:N
j = sheet(1,:);
P_k(1,n)*real(trace(Rkk(:,1:M1+1,n)*V1)) >= theta(1,n)*delta_noise + (Omega(1,j)*P_k(j,n))*(0.25*(pow_pos(theta(1,n)+real(trace(Rkk(:,1:M1+1,n)*V1)),2))+0.25.*pow_pos((theta_ini(1,n)-real(trace(Rkk(:,1:M1+1,n)*V_ini))),2)-0.5*(theta_ini(1,n)-real(trace(Rkk(:,1:M1+1,n)*V_ini))).*(theta(1,n)-real(trace(Rkk(:,1:M1+1,n)*V1))));
end
%k = 2
for n = 1:N
j = sheet(2,:);
P_k(2,n)*real(trace(Rkk(:,M1+2:M1+12,n)*V1)) >= theta(2,n)*delta_noise + (Omega(2,j)*P_k(j,n))*(0.25*(pow_pos(theta(2,n)+real(trace(Rkk(:,M1+2:M1+12,n)*V1)),2))+0.25.*pow_pos((theta_ini(2,n)-real(trace(Rkk(:,M1+2:M1+12,n)*V_ini))),2)-0.5*(theta_ini(2,n)-real(trace(Rkk(:,M1+2:M1+12,n)*V_ini))).*(theta(2,n)-real(trace(Rkk(:,M1+2:M1+12,n)*V1))));
end
%k = 3
for n = 1:N
j = sheet(3,:);
P_k(3,n)*real(trace(Rkk(:,M1+13:M1+23,n)*V1)) >= theta(3,n)*delta_noise + (Omega(3,j)*P_k(j,n))*(0.25*(pow_pos(theta(3,n)+real(trace(Rkk(:,M1+13:M1+23,n)*V1)),2))+0.25.*pow_pos((theta_ini(3,n)-real(trace(Rkk(:,M1+13:M1+23,n)*V_ini))),2)-0.5*(theta_ini(3,n)-real(trace(Rkk(:,M1+13:M1+23,n)*V_ini))).*(theta(3,n)-real(trace(Rkk(:,M1+13:M1+23,n)*V1))));
end
for i = 1:M1+1
V1(i,i)==1;
end
cvx_end
r = r+1;
theta_ini = theta;
V_ini = V1;
[eig_vec,eig_value]=eig(V_ini);
eig_max=max(max(eig_value));
[row,column]=find(eig_value==eig_max);
u = eig_vec(:,column);
P_out = V1;
theta_out = theta;
Rate1 = K*phi_sum;
sum_rate = [sum_rate Rate1];
end
i = 1;
end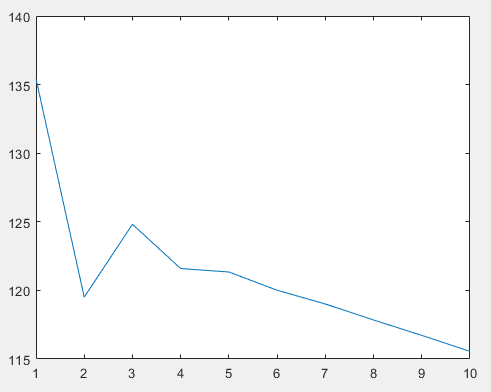
the results are shown as this photo
Are you employing a Successive Convex Approximation (SCA) algorithm? If so, its behavior is out of scope for this forum. Crude SCA, not using line search or trust region, is generally unreliable, and there are generally no guarantees on its behavior. In any event, you have some non-obvious iterative scheme, involving eigenvalue decompositions which I have no idea what’s it’s doing at a higher level mathematically.
Also, you have not provided a reproducible problem, because you haven’t shown the values of hb,hk,P_k .