I am solving semi definite relaxed problem using CVX and I want to initialise CVX variables using warm start. As the initial point matter in my problem so is there any way to give a warm start in CVX. I have seen some links where warm start is given in cvxpy case. But I can not find anything related to CVX related.
Warm start (of CVX variables or expressions) is not possible in CVX.
However, I don’t know why you think the initial point matters in an SDP problem, unless you are using a higher level iterative process on top of CVX, such as SCA. If using SCa, you would need to provide a starting point, as that is input data to CVX, not a CVX variable.
Yes, to be exact, I am using the Taylor series approximation above CVX and running CVX for many iterations until we reach convergence.
Let’s say that I have this SDP problem.
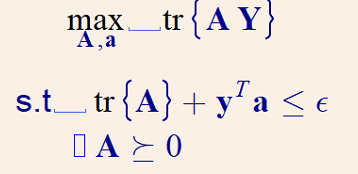
In this problem, I need to apply a warm start to give a starting point for both A and a as A_init and a_init.
If A and a are the only optimization variables for each CVX subproblem, and everything else is input data, then no warm start is needed to CVX.
Perhaps Y and/or y are iteratively updated prior to each CVX subproblem? Maybe you are referring to that as warmstarting? From the viewpoint of CVX, that is not warm starting its optimization variables, because Y and y would be input data to CVX.
If that does not describe your situation, you need to make clear what your original problem is, what your Taylor series approximation is (applied to what), and what is iteratively updated at the level above (i.e., outside) CVX, and what are the CVX (optimization) variables in each CVX subproblem.
Thanks for your answer.
Let’s make things clear with a formulation.
CVX is called inside a loop that implements a sequential programming algorithm. Here is the problem that we solve at each iteration of the inner program as defined in https://www.jstor.org/stable/169728:
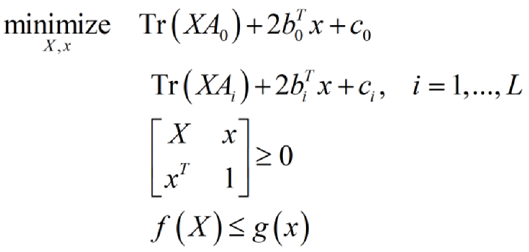
We used the notation in Semidefinite Programming Relaxations of Non-Convex Problems in Control and Combinatorial Optimization.
The function f(X) is convex in X. The function g(x) is not convex in x but is approximated by a convex function, according to A General Inner Approximation Algorithm for Nonconvex Mathematical Programs on JSTOR, at each algorithm iteration.
Since the optimization variables X and x are not independent, we need to appropriately initialize them to avoid obtaining an unfeasible solution from CVX at the first iteration of the algorithm, which will stop the algorithm. The function that is iteratively approximated by a convex function is g(x).
How can we input initial values X0 and x0 to the iterative optimization algorithm?
Perhaps you need to read up on the basics of Sequential Convex Programming (Approximation). You need to pick a starting value about which to do the initial linearization (or convexification). How to pick a good starting value is out of scope of this forum, and is not necessarily easy. The point about which to do the convexification for the next iteration is based on the solution to the CVX problem in the first iteration. In general, if you don’t know what you’re doing, you should not be surprised if the overall algorithm fails. At no point are CVX (declared) variables ever warm started.
CVXPY has some built-in Convex-Concave Procedure capabilities. Maybe you should use those if applicable GitHub - cvxgrp/dccp: A CVXPY extension for convex-concave programming .