Variable normalization in a cvx optimisation problem

1

Hello everybody,

I am working with an optimisation problem as the following:
MOP

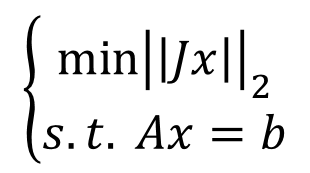
where J is a T x N matrix, x is a one-column vector with dimension n, A is a M x N matrix and b is a one-column vector with dimension M.

I try to solve it using cvx with the following sequence:

cvx_begin
    variable x(NNodes); 
    minimize ((norm(J*x,2)));
    subject to
        A*x == b;   
cvx_end

My question is related to get a solution of this problem. In most cases, when I work with a problem like this, I have to normalise all matrices by the frobenius norm of one of them to get a good solution. But this does not always work (it even produces different results depending on the frobenius norm that I use, i.e. the solution if I use the frobenius norm of J is different than if I use the frobenius norm of A. In addition, in some cases it is not necessary to normalize any matrix.

I can not understand why normalise by one or the other matrix produces different solutions. The problem is essentially the same regardless of the solution (as far as I understand). Can somebody help me with this issue?

Thanks,
Jose

2

That doesn’t seem like a CVX question. I think a more general forum like https://math.stackexchange.com/ or similar would be more appropriate for a question at this level of generality.

Here we prefer to use concrete, reproducible code samples, so if you think you have two reproducible examples of CVX code which you think should give the same answer, but don’t, then please share them and explain exactly what the problem is.

At the moment it is not clear how your normalization works so it is hard to answer concretely. Surely if you multiply A,b by the same constant and J by any constant (all constants nonzero) then you have a mathematically equivalent problem, but due to numerics even then you don’t need to get the exactly identical solution. So more details and reproducible code would be helpful.