Uncertainty set declaration

MIDCP
1

I have formulated a subproblem based on an uncertainty set defined by d. It is a robust optimization problem. I have a confusion that should I include d as a variable and impose equality constraint or put it as expression. However I know for sure that d is an optimization variable. Also when I input some optimal value z* from Master problem the value of g turns negative.

Screenshot%20(200)
Screenshot (200).png969×534 38.6 KB

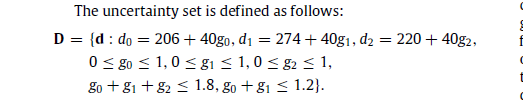
Screenshot%20(202)

    m = 3; % Number of facility locations
    n = 3; % Number of customers
    
    %Fixed cost of the building facilities at site i, f(i)
    f = [400; 414; 326];
    
    %Unit capacity cost a(i), i = 1,....,m
    a = [18; 25; 20];
    
    %Unit transportation cost c(ij), i = 1,....,m; j = 1,....,n
    c = [22 33 24; 33 23 30; 20 25 27];
    
    %Forecast demand df(j)
    df = [206; 274; 220];
    
    %Maximal demand deviation dm(j)
    dm = [40; 40; 40];
   
    
    %Capacity variable z*(i) , obtained from master problem
    zo_set = [772; 0; 0];
    lb = zeros(3,1); ub = ones(3,1);
    
    
    for i = 1:m
        for j = 1:n
            M1(i,j) = min(df(j)+dm(j),zo_set(i));  %M1(i,j) == min(df(j)+dm(j),zo(i)) for every i,j
        end
    end
    
    
    for i = 1:m
        M2(i) = max(c(i,:))               %M2(i) == max(c(i,j)) for every i
    end
    
    
    for j = 1:n
        M3(j) = max(c(:,j))               %M3(j) == max(c(i,j)) for every j
    end
           
   

    cvx_begin
        cvx_solver gurobi
        variable x(3,3) nonnegative;
        variable u(3) nonnegative;
        variable v(3) nonnegative;
        variable p(3,3) binary;
        variable q(3) binary;
        variable r(3) binary;
        variable d(3);
        variable g(3);
        
         
        
        objS = sum(sum(c.*x));
        maximize (objS);
        subject to
            %Demands calculated by introducing uncertainty
            d == df + g .* dm;
            sum(g) <= 1.8;
            g(1)+ g(2)<= 1.2 ;
            g(:) >= lb; g(:) <= ub;

                    
        
            %Capacity Constraints (Primal feasibilty)
            for i= 1:m
                sum(x(i,:)) <= zo_set(i);
            end

            % Demand Constraints (Primal feasibilty)
            for j= 1:n
                sum(x(:,j)) >= d(j)
            end

            % Dual feasibility Constraints
            for  i = 1:m
                for j = 1:n
                    v(j) - u(i) <= c(i,j)
                end
            end

            %M1 constraints
            for i = 1:m
                for j = 1:n
                    x(i,j) <= M1(i,j) .* p(i,j)
                end
            end
            
            for i = 1:m
                for j = 1:n
                    c(i,j) - v(j) + u(i) <= (c(i,j) + M2(i)) .* (1 - p(i,j))
                end
            end


            % M3 constraints    
            for j = 1:n
                v(j) <= M3(j).* q(j)
            end

            for j = 1:n
                sum(x(:,j)) - d(j) <= dm(j) .* (1 - q(j))
            end

            % M2 constraints 
            for i = 1:m
                u(i) <= r(i) .* M2(i) ;
            end  

            
            for i = 1:m
                zo_set(i) - sum(x(i,:)) <= (1 - r(i)) .* zo_set(i);
            end  
            
            
    cvx_end

Please let me know how to fix the issue. For the given z* , I get positive value of g but for second iteration g becomes negative.

2

What second iteration? You shiw a program which invokes CVX once, i.e., to solve one optimization problem.

3

Basically I am implementing column and constraint generation algo for location-transportation problem based on the paper https://www.sciencedirect.com/science/article/abs/pii/S0167637713000618
This is how the master problem looks like. The convergence reaches at 2nd iteration so I manually fed the values for 2nd step just to verify my code and somehow at second step when I feed values of d* from subproblem to master problem, the master problem solves to correct lowerbound but the z* obtained from masterproblem at second iteration when fed to subproblem doesn’t give same value as LB. Meaning LB should be equal to UB for convergence.

Screenshot%20(204)
Screenshot (204).png874×571 51.1 KB 

    dmax = Uncertainty_constraint(df,dm);

cvx_begin
cvx_solver gurobi
variable y(3) binary;
variable z(3) nonnegative;
variable x(3,3,k) nonnegative;
variable eta;

    obj = 0;
    for i = 1:m
        obj = obj + f(i).*y(i)+ a(i).*z(i);
    end
    minimize (obj + eta);
    subject to
        % Hidden z constraints
        %To address the feasibility issue, the below constraint is added
        % sum(z(i)) >= max(sum(d(j)): d?D)

        sum(z) >= sum(dmax);
        i = 1:m;
        z(i) <= 800 .* y(i);


        %eta constraint
        
            sub = 0;
            for i = 1:m
                for j = 1:n
                    sub =  sub + c(i,j)'*x(i,j,:);
                end
            end

            eta >= sub;

% eta >= sum(sum(c.*x));

            for j = 1:n
                sum(x(:,j,:)) >= d(j,:);
            end
            
         
            for i = 1:m
                sum(x(i,:,:)) <= z(i);
            end
  cvx_end

function [dmax] = Uncertainty_constraint(df,dm)
m = 3; % Number of facility locations
n = 3; % Number of customers
lb = zeros(3,1); ub = ones(3,1);
% %Forecast demand df(j)
% df = [206 274 220];
%
% %Maximal demand deviation dm(j)
% dm = [40 40 40];

    cvx_begin

            cvx_solver gurobi
            variable dmax(3);
            variable g(3);
            
            maximize(sum(dmax));
            subject to
                dmax == df + g .* dm;
                sum(g) <= 1.8;
                g(1)+ g(2)<= 1.2 ;
                g >= lb; g <= ub;

    cvx_end

end

I think it is some issue in the way I wrote some constraints that caused this issue. I just want to conform if I have written the formulation correctly as the screenshots. The flow of the values would fix itself if the formulation is correct. If you could help me with that it would be great. Thanks!

4

This is a bit beyond my energy level at present. One suggestion is trying Mosek as solver if you can. There have been some issues with bugs in the CVX/Gurobi interface (I don’t know whether they have all been resolved in CVX 2.1Gurobi 9.0), so trying Mosek could at least determine whether the issue is with CVX/Gurobi combination.

If you want more general guidance/feedback on the algorithms in the paper, under what circumstances they converge, work, etc., perhaps try https://or.stackexchange.com/

5

Ok thank you so much @Mark_L_Stone