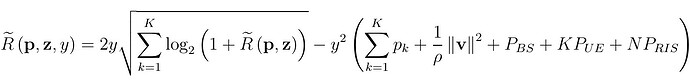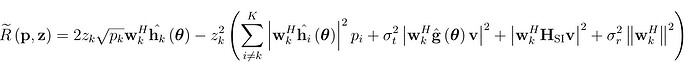The term inside log is concave only, but it is showing log(convex) while running the code

[Kagana_Sarath_babu]

This is the code: optimization variable is P_rand(K)

transmit_rate(k)=j*log(1+2*sqrt(P_rand(k)).*z(k).*(real( (w_k(:,k)'*h_theta(:,k)))) - (z(k)^2).*(b + c(k)*sigma_sqr_t+d(k)+e(k)*sigma_sqr));

Error obtained as follows:

Error using cvx/log
Disciplined convex programming error:
Illegal operation: log( {convex} ).

Error in objective_power (line 24)
transmit_rate(k)=j*log(1+2*sqrt(P_rand(k)).*z(k).*(real( (w_k(:,k)'*h_theta(:,k)))) - (z(k)^2).*(b + c(k)*sigma_sqr_t+d(k)+e(k)*sigma_sqr));

Error in Opt_UplinkPower (line 103)
[obj_power] = objective_power(K,w_k,h_theta,P_opt,g_theta,h_s_i,v,sigma_sqr_t,sigma_sqr,rho,P_BS,P_UE,P_RIS,y,z);

Please help me in this

[Mark_L_Stone]

Maybe something negative is multiplying the sqrt, making it convex?

[Kagana_Sarath_babu]

This term 2*sqrt(P_rand(k)).z(k).(real( (w_k(:,k)'h_theta(:,k)))) is concave and it is not multiplying with negative and the second term (z(k)^2).(b + c(k)*sigma_sqr_t+d(k)+e(k)*sigma_sqr) is linear one

The overall function is log(1+concave-affine)

[Kagana_Sarath_babu]

I think Mosek optimization tool can handle this kind of problems?

[Kagana_Sarath_babu]

The main objective function is given as follows:

Where

According to the knowledge from the convex text book by boyd, the above function is concave only and max {concave} with convex constraints becomes convex optimization problem.

Cvx is saying that log{convex}, but it is log{conave} only

Anyone can plz resolve this

[Mark_L_Stone]

Please show complete reproducible code, complete with all input data.

Are you using CVX 2.2? Do not use CVX 3.0beta, which has bugs, including producing error messages for some correct code and not correctly processing all constraints. Use cvx_version to determine which version of CVX you are using.

[Kagana_Sarath_babu]

I have provided all the inputs properly.

---

CVX: Software for Disciplined Convex Programming (c)2014 CVX Research
Version 2.2, Build 1148 (62bfcca) Tue Jan 28 00:51:35 2020

Installation info:
Path: D:\cvx
MATLAB version: 9.14 (R2023a)
OS: Windows 10 amd64 version 10.0
Java version: 1.8.0_202
Verfying CVX directory contents:
WARNING: The following files/directories are missing:
D:\cvx\sedumi.travis.yml
These omissions may prevent CVX from operating properly.
Preferences:
Path: C:\Users\User_1\AppData\Roaming\MathWorks\MATLAB\cvx_prefs.mat
License host:
Username: User_1
Host ID: 489ebda31825 (eth1,10.13.2.52)
Installed license:
No license installed.

[Mark_L_Stone]

Now please show complete reproducible code, complete with all input data.

[Kagana_Sarath_babu]

Complete code:

for iter = 1 : N_iter
p = iter;

            % Update y (eq.2) and z_k (eq.4)
            [SINR,SINR_sqr,~,sum_rate] = Data_rate(K,w_k,h_theta,P_rand,g_theta,h_s_i,v,sigma_sqr_t,sigma_sqr);

            y=sqrt(sum_rate)/(sum(P_rand)+( (1/rho)*norm(v)^2)+P_BS + P_UE + P_RIS);
            z=SINR_sqr;

            cvx_begin %quiet

            variable P_opt(K)
            
            % Compute objective function (eq.5)
             [obj_power] = objective_power(K,w_k,h_theta,P_opt,g_theta,h_s_i,v,sigma_sqr_t,sigma_sqr,rho,P_BS,P_UE,P_RIS,y,z);
             obj = obj_power;
            
            maximize real(obj)
            
            % constraints

            % Target sensing constraint (eq.6)
            temp = 0;
            for k = 1:K

            temp = temp + (norm(w_0'*h_theta(:,k))^2)*(P_opt(1));
            
            end
        
            Gamma_t*( temp + norm(w_0'*h_s_i*v)^2 + sigma_sqr*(norm(w_0')^2) )...
                 <= sigma_sqr_t*(norm(w_0'*g_theta*v)^2);

            % Individual Rate constraint (QoS) (eq.7)
            
            for k=1:K
            a = (norm(w_k(:,k)'*h_theta(:,k))^2)*P_opt(k);
            b=zeros(1,1);
            for mm=1:K
                if mm~=k
                    b =  b + (norm(w_k(:,k)'*h_theta(:,mm))^2)*P_opt(mm);
                    %b1(:,k) = b;
                end
            end
            c(k) = norm(w_k(:,k)'*g_theta*v)^2;
            d(k) = norm(w_k(:,k)'*h_s_i*v)^2;
            e(k) = norm(w_k(:,k)')^2 ;

            (2^(R_min)-1)*( b + c(k)*sigma_sqr_t + d(k) + e(k)*sigma_sqr)...
                     <= a;               

            end

            % Individual Power Constraint (eq.8c)
            for k = 1:K

               P_opt(k) <= P;

               P_opt(k) >= 0;
            end

        cvx_end

        % cvx_status 

        if strcmp(cvx_status,'Solved') || strcmp(cvx_status,'Failed') || strcmp(cvx_status, 'Inaccurate/Solved')

            P_rand = P_opt;

        else

            P_opt = P_rand;   % default value

        end
        
        % compute objective function

        %[main_obj] = objective_main(K,w_k,h_theta,P_opt,g_theta,h_s_i,v,sigma_sqr_t,sigma_sqr,rho,P_BS,P_UE,P_RIS);
        % obj = obj_power;
        [obj_power] = objective_power(K,w_k,h_theta,P_opt,g_theta,h_s_i,v,sigma_sqr_t,sigma_sqr,rho,P_BS,P_UE,P_RIS,y,z);
            
        J(p) = real(obj_power);

        % test stopping criterion

        if N_iter > 1

            abs(J(N_iter) - J(N_iter-1)) <= tol;

            break;
        end
   
  end

And the function related to objective function is shown below:

function [obj_power] = objective_power(K,w_k,h_theta,P_rand,g_theta,h_s_i,v,sigma_sqr_t,sigma_sqr,rho,P_BS,P_UE,P_RIS,y,z)

% Calculating the terms related to an objective function of Uplink transmit power optimization
for k=1:K
a(k) = 2*sqrt(P_rand(k)).z(k).(real( (w_k(:,k)'*h_theta(:,k))));

            b=zeros(1,1);
            for mm=1:K
                if mm~=k
                    b = b + (norm(w_k(:,k)'*h_theta(:,mm))^2)*P_rand(mm);
                    %b1(:,k) = b;
                end
            end
            %b1(:,k) = b;
            c(k) = norm(w_k(:,k)'*g_theta*v)^2;
            d(k) = (norm(w_k(:,k)'*h_s_i*v)^2);
            e(k)= norm(w_k(:,k)')^2 ;
            f(k)= (z(k)^2).*(b + c(k)*sigma_sqr_t+d(k)+e(k)*sigma_sqr); % SINR
            r(k)= a(k)- f(k); % 
            j=log(2);
            transmit_rate(k)=j*log(1+2*sqrt(P_rand(k)).*z(k).*(real( (w_k(:,k)'*h_theta(:,k)))) - (z(k)^2).*(b + c(k)*sigma_sqr_t+d(k)+e(k)*sigma_sqr));
        end
        sum_rate=sum(transmit_rate);
        
        obj_power=2*y*sqrt(sum_rate)-((y^2)*( sum(P_rand)+( (1/rho)*norm(v)^2 ) + P_BS + P_UE + P_RIS));

end

i am getting error at the line:

transmit_rate(k)=jlog(1+2sqrt(P_rand(k)).z(k).(real( (w_k(:,k)'h_theta(:,k)))) - (z(k)^2).(b + c(k)*sigma_sqr_t+d(k)+e(k)*sigma_sqr));

[Mark_L_Stone]

You have not provided reproducible code. For instance, P_rand, which is the argument of log, is not provided.

Have you placed statements just prior to where the error message occurs, which each consist just of the variables, expression and subexpressions generating the error, and see what CVX says about them?

Do you get the error message on the first iteration of the for loop which calls CVX? Or on some later iteration.

You need to show a matched set of reproducible code and error message from running it. Some forum posters show an error message which corresponds to a different version of the code than they show - that does not make it as easy as it should be for people to help them.

[Mark_L_Stone]

Did you insert the statements I told you to so that you can see what CVX thinks all the pieces are? Did you examine the optimal values from the iteration just prior to the iteration in which the error occurred, and see what therefore was provided as input in the iteration which had the error?

The path of the optimization algorithm, and the occurrence or not of the error, might depend on the solver and settings used. Even a slight difference in the solution, or a different optimal solution if not unique, can cause SCA to take an entirely different path.

CVX 2.2 seems fairly reliable at giving an error message when its rules are violated. But the error message isn’t always informative as to what the true error is. That is due to CVX’s internal design. Certain errors propagate for a while before they become “fatal”, and the error message at the time of fatality might not be the true underlying cause. I don’t know whether that’s happening in your case. I.e., maybe there really is a DCP vio9lation in the statement triggering the error message, but it might not really be log(convex).

You shouldn’t assume that your SCA is stable,reliable, or converges to anything. You might get lucky. You might not. Perhaps the optimal values in one iteration results in input data for the next iteration which causes something to be non-convex, or at least violate CVX’s rules. As a simple example, if you have a*x^2 with a being the optimal value from the previous iteration, perhaps you expect it to be positive; but then in one iteration it comes out negative, in which case in the next iteration, a*x^2 will suddenly be concave and trigger a CVX error.

[Kagana_Sarath_babu]

Perhaps the optimal values in one iteration results in input data for the next iteration which causes something to be non-convex, or at least violate CVX’s rules,

Related to this statement,
transmit_rate(k)=jlog(1+2sqrt(P_rand(k)).z(k).(real( (w_k(:,k)'h_theta(:,k)))) - (z(k)^2).(b + c(k)*sigma_sqr_t+d(k)+e(k)*sigma_sqr));

Exactly Sir, you are true regarding this statement. For the next iteration, the objective ‘transmit_rate’ becomes log{convex} as real( (w_k(:,k)'*h_theta(:,k))) becomes negative . I have observed this by running the code Sir.

What needs to be done to avoid this situation Sir?

[Mark_L_Stone]

Don’t use a crude SCA algorithm not having adequate safeguards, such as needed bounds on variables, or perhaps trust region or line search. At some point you might as well use a high quality off-the-shelf non-convex optimizer, such as can be called from YALMIP.

[Kagana_Sarath_babu]

Happy to inform that my issue has been resolved Sir.
The point where you have mentioned log{convex} is correct and observed also in my code.

For the next iteration, it is becoming negative (hence convex) then CVX stops working. I have rectified the error and my code is giving optimized values without taking any iterations also. I have another question that will be asked as a separate topic.

Thanks for your help in this regard sir

[Kagana_Sarath_babu]

Same MATLAB version and same cvx version is used in two different systems.
One system is giving optimized values and producing graphs, but another system is giving unbounded/Infeasible/failed???
What is the reason sir? How to resolve this issue?

[Michal_Adamaszek]

Borderline/barely solving problems can easily tip over to one side (solved) or the other side (not solved) depending on the circumstances. Different OS/hardware/number of threads etc. is certainly one such contributing circumstance because it affects the order of floating point operations. So it is just evidence that your problem is very borderline. Especially if you do it in a loop and differences accumulate.

[Kagana_Sarath_babu]

What do you mean by Borderline/barely problems???

Then we can think about using cvx for optimization problem?
And I observed that even when the solution status is “Failed” , cvx is giving Optimal value.
How it is possible???