The status is solved, but the result is wrong

[Kim]

Pseudo code for my problem

clear, clc

%Known information(Transfer function, E-field)
h=[1; 2; 3; 1; 2; 3; 1; 2];

%constant
sigma=1;
law=1000;
SAR=3;
P=1;
R=50;
%Number of frequency, antenna
N=1;
M=8;
err=1;
t=1;
t0=0.1;
ini=1;
count=1;
xor=1;

% cvx_solver mosek

%Entire optimization process
while xor
%Initialize S (by Time-reversal)

if ini==1
     S=[1; 2; 3; 1; 2; 3; 1; 2];

    %Calculate g using signal & transfer function
    for j=1:1:N
        x=1;
        y=1;
        for i=1:1:M*(M+1)/2
            if i<=M
                G(i,j)=2;
            else
                y=y+1;
                G(i,j)=1;
                if y>=M
                    x=x+1;
                    y=x;
                end
            end
        end
    end
    
end

%Calculate gambma using updated result
gambma=G/sum(sum(G))

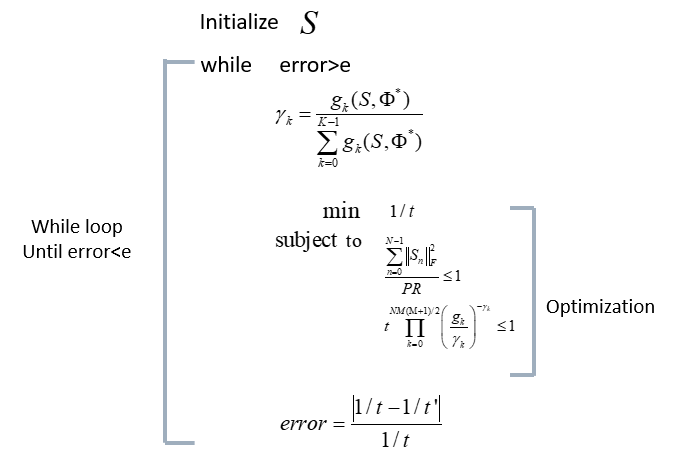
% Optimization function begin GP
cvx_begin gp

    variable s(M, N)
    variable t
    
    %To prevent cvx to double error
    expression h(M, N)
    expression g(M*(M+1)/2, N)
    
    %Known information(Transfer function, E-field)
    h=[1; 2; 3; 1; 2; 3; 1; 2];
    
    %Calculate g using s(signal) & h(transfer function)
    for j=1:1:N
        x=1;
        y=1;
        for i=1:1:M*(M+1)/2
            if i<=M
                g(i,j)=(h(i,j)^2)*(s(i,j)^2);
            else
                y=y+1;
                g(i,j)=2*h(x,j)*h(y,j)*s(x,j)*s(y,j);
                if y>=M
                    x=x+1;
                    y=x;
                end
            end
        end
    end
            
    product=(g./gambma).^(-gambma)
    
    %Optimization begin
    min 1/t
    subject to
    
        t*prod(prod(product))<=1;                                  
        (norm(s, 'fro'))^2/(P*R)<=1
        
cvx_end
s0=s
G=g
ini=0;
count=count+1;
err=abs((1/t-1/t0)/(1/t))
t0=t
xor=xor((err>0.1), (count<6));



%Check optimum value
sub=(norm(s0, 'fro'))^2/(P*R)
SIGMA=t/(sum(sum(G)))
PRODUCT=t*prod(prod(product))

end

Result

Successive approximation method to be employed.
Mosek will be called several times to refine the solution.
Original size: 121 variables, 9 equality constraints
8 exponentials add 64 variables, 40 equality constraints

Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Solved

Status: Solved
Optimal value (cvx_optval): +0

The problem is simple GP problem (I think…)
The above result shows my question.

As you can see, the status is solved so I thought that my problem is solved well.
However the optimal value is +0 that I didn’t expected and the optimal variable is wrong also!
So I don’t know what does the status of my problem mean…

Please give me any comment or advice…

[Kim]

Plus,
In my optimization problem, there are two variable, s(M,N) and t
There’s while loop so optimization problem runs several time.
However s(M,N) isn’t changed, only t is changed each loop.

So my question is this.
There are two variable, s(M,N) and t by the way why only t is changed?

[Mark_L_Stone]

min 1/t
just prints out a meaningless number, and is not contributing to the specification of your optimization problem - i.e., it is essentially ignored by CVX. So you have just been solving a feasibility problem, even though that is not your intention.

You want
minimize(1/t)
But you might as well use
maximize(t)
instead.

I haven’t checked the rest of what you did, so this may not be the only error in your code.

Given you use of gp mode, I recommend you follow the advice at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions .

[Kim]

Thank you so much for your reply.
I tried that you comment to me (change objective function). Unfortunately, the result is same.

There are some question.

1. Basic solvers ,mosek and sedumi, have many errors on GP because of Successive Approximation? so you recommend cvxquad?
2. I don’t know why the status is ‘solved’ even the result is unreliable. Is there any case like this?

[Kim]

min 1/t
subject to

    t*prod(prod(product))<=1;                                  
    (norm(s, 'fro'))^2/(P*R)<=1

This is my optimization problem. As you can see, very simple.
There are two constraints but only the first one is tightly bounded the second one is loosely bounded. Is there any reason?

[Joachim_Dahl]

This problem looks so simple that you should be able to solve it using MOSEK Fusion easily. There are many examples in the documentation on how to solve similar problems. That will give you a reference without the approximation scheme used in CVX, and the solution will almost certainly be more accurate.

[Kim]

Thank you so much.
However I’ve been using MOSEK solver. MOSEK Fusion is different with MOSEK solver?

[Mark_L_Stone]

Please follow @Joachim_Dahl’s advice. MOSEK fusion provides a way to call MOSEK directly without using CVX at all. If you proceed on that route and need any further help, then you should seek it at https://groups.google.com/forum/#!forum/mosek rather than this forum, as MOSEK fusion not involve use of CVX.

However, in answer to your questions.

min 1/t doesn’t t do anything in CVX. You need to use minimize to specify an objective function to be minimized, not min. Until you make this change, you are only specifying and solving a feasibility problem, not minimizing an objective subject to constraints.

CVXQUAD’s Pade Approximation is much more reliable than CVX’s Successive Approximation method. However, MOSEK 9’s native exponential cone capability, which is not (yet) available under CVX, should be faster and even more reliable than using CVXYQAD with MOSEK solver under CVX.

I was “locally” forgetting you are using gp mode, so minimize(1/t) is o.k., but minimize(inv_pos(t)) also works. maximize(t) would also work.

[Kim]

Wow I just mistook trivial things…
My code operates well after changing min to minimize.

Thank you so much for your comment!