The Optimization problem is a SOCP problem. CVX works fine (Nans sometimes appear).When I bring it back, it satisfies all the constraints, but it’s very different from my objective function, in other words, it doesn’t minimize the objective function.
Here’s my code:
Sometimes it has no solution:
Calling SDPT3 4.0: 1606 variables, 776 equality constraints
For improved efficiency, SDPT3 is solving the dual problem.
num. of constraints = 776
dim. of sdp var = 2, num. of sdp blk = 1
dim. of socp var = 1594, num. of socp blk = 5
dim. of linear var = 6
dim. of free var = 3 *** convert ublk to lblk
SDPT3: Infeasible path-following algorithms
version predcorr gam expon scale_data
HKM 1 0.000 1 0
it pstep dstep pinfeas dinfeas gap prim-obj dual-obj cputime
0|0.000|0.000|3.0e+01|5.1e+00|2.9e+03| 1.100000e+01 0.000000e+00| 0:0:00| chol 1 1
1|0.938|0.680|1.8e+00|1.7e+00|5.7e+02| 6.901705e+00 -1.955824e+01| 0:0:00| chol 1 1
2|1.000|0.954|2.2e-06|8.0e-02|4.1e+01| 3.396503e+00 -1.547509e+01| 0:0:01| chol 1 1
3|0.952|0.923|9.3e-07|6.5e-03|4.6e+00|-6.540527e+00 -9.904196e+00| 0:0:01| chol 1 1
4|0.890|0.847|5.8e-07|1.0e-03|6.1e-01|-9.077469e+00 -9.581009e+00| 0:0:01| chol 1 1
5|0.293|0.448|4.1e-07|5.7e-04|3.5e-01|-9.158024e+00 -9.420073e+00| 0:0:01| chol 1 1
6|0.197|0.382|3.3e-07|3.5e-04|2.4e-01|-9.216413e+00 -9.367807e+00| 0:0:01| chol 1 1
7|0.162|0.406|2.8e-07|2.1e-04|1.7e-01|-9.288524e+00 -9.360453e+00| 0:0:01| chol 1 1
8|0.140|0.338|2.4e-07|1.4e-04|1.4e-01|-9.393390e+00 -9.403684e+00| 0:0:01| chol 1 1
9|0.107|0.121|2.1e-07|1.2e-04|1.4e-01|-9.719935e+00 -9.417867e+00| 0:0:01| chol 1 1
10|0.155|0.370|1.8e-07|7.4e-05|2.0e-01|-9.773111e+00 -9.616128e+00| 0:0:02| chol 1 1
11|0.270|0.135|1.3e-07|6.4e-05|2.3e-01|-1.141006e+01 -9.651558e+00| 0:0:02| chol 1 1
12|0.318|0.062|9.6e-08|6.0e-05|2.2e+00|-4.630663e+01 -9.717235e+00| 0:0:02| chol 1 1
13|0.030|0.029|9.3e-08|5.8e-05|1.1e+01|-4.360920e+02 -9.699650e+00| 0:0:02| chol 1 1
14|0.005|0.010|1.7e-07|5.7e-05|6.5e+01|-3.962860e+03 -9.705473e+00| 0:0:02| chol 1 1
15|0.002|0.003|1.4e-06|5.7e-05|5.0e+02|-3.574752e+04 -9.707089e+00| 0:0:02| chol 1 1
16|0.002|0.012|2.7e-06|5.7e-05|8.4e+02|-3.234082e+05 -9.713862e+00| 0:0:02| chol 2 2
17|0.000|0.000|5.1e-06|5.7e-05|7.2e+03|-2.912615e+06 -9.714055e+00| 0:0:02| chol 2 2
18|0.000|0.002|7.2e-05|5.7e-05|2.1e+04|-2.629098e+07 -9.715258e+00| 0:0:03| chol 2 2
19|0.000|0.000|3.5e-04|5.7e-05|1.7e+05|-2.369863e+08 -9.715451e+00| 0:0:03| chol 2 2
20|0.000|0.000|6.4e-04|5.7e-05|5.1e+05|-9.657608e+08 -9.717037e+00| 0:0:03| chol 2 2
21|0.000|0.000|8.3e-04|5.7e-05|6.2e+05|-1.187261e+09 -9.718033e+00| 0:0:03|
stop: progress is too slow
prim_inf,dual_inf,relgap = 8.32e-04, 5.66e-05, 5.24e-04
sqlp stop: dual problem is suspected of being infeasible
number of iterations = 21
residual of dual infeasibility
certificate X = 1.04e-09
reldist to infeas. <= 2.69e-15
Total CPU time (secs) = 2.97
CPU time per iteration = 0.14
termination code = 2
DIMACS: 6.4e-04 0.0e+00 3.0e-04 0.0e+00 -1.0e+00 5.3e-04
Status: Infeasible
Optimal value (cvx_optval): +Inf
It appears you are using some type of crude (unsafeguarded) Successive Convex Approximation (SCA), which may be unstable, and is perhaps producing some infeasible problems. You may be better off using an off-the-shelf non-convex nonlinear optimizer.
You might improve the numerical stability of an individual optimization problem a little by changing to norm(f) <= sqrt(Pt) which might be better conditioned.
Bu fundamentally, SCA might not converge at all, might produce infeasible problems along the way, might diverge with larger and larger magnitude inputs and optimal solutions, and other bad things. if it does converge to anything, it is not necessarily even a local, let alone global, optimum of the original problem. But it might work, depending on the input data, and crucially, depending on the starting value of the variable9s) being iteratively updated.
Papers are full of cockamamie algorithms which often don’t work well in practice. Sometimes, the authors have to hunt for input data and starting values which make it work fo ran example in the paper. Or they only tried it on a problem for which they were lucky.
Also in the future, please copy and paste code using Preformattted text icon, rather than posting image of the code.
Thanks a lot.I tried to convert the constraints to first order, but the results were still terrible
Looking more carefully at your program, I don’t understand what it does.
it appears that no matter how many times the while loop is executed, there are only ever 2 distinct optimization problems solved. The first time through the loop, p_n has the value to which p was initialized. The 2nd time through the loop, p_n has the value to whichp was set at the end of the first time through the loop, but that value has nothing to do with the results of the optimization problem which was just solved. That value of p does not appear to depend on anything which happened earlier in that time though the loop , .e., it is always set to the same thing. So that 2nd value of p_n will be the same for the 3rd and subsequent times through the for loop,. Hence, the CVX optimization problem instance is the same for the 2md, 3rd, 4th, etc. time through the loop.
Sorry, I didn’t optimize the program very well. Here the second subproblem is LS problem about p. The paper uses alternating minimization method to optimize variables f and p. In LS problem, the value of p is related to f (f1 + f2 + f3 =S* f).In line 96 of the code, I update the value of p.
Well, I guess you didn’t show all the code, such as where p gets optimized, because in the code you showed, other than the first time through the loop,it is set to value which appears to depend only on constants. Anyhow, alternating minimization can be precarious.
Thank you for your reply. But in line 96 of the code: p = pinv(D*A)D Fi S F, where p is optimized. It’s a direct application of the LS problem.
That is how I incorrectly read your code for my first post. Hence my referring to it being SCA (I incorrectly read p as a least squares solution whose input involved the just solved CVX optimization problem.
But that is not the code you showed in your original post, which is
p = pinv(D*A)*D*fi*(f1+f2+f3);
That does not involve the optimization variable f, and therefore is a constant. Hence, my 2nd post, which was based on my more carefully reading your code and seeing that f did not appear on the RHS of the assignment for p.
So now that you have shown the “correct” code, you are left with an alternating optimization algorithm. I don’t know what the paper says about provable convergence, stability, etc. of that algorithm, but many such algorithms do not reliably converge for all problems.
BTW, kudos for using pinv(A)*b to solve least squares problem A\b. That immediately became my favorite way of solving linear least squares problems when I first used an ancient version of MATLAB (written in FORTRAN) 40 1/2 years ago.
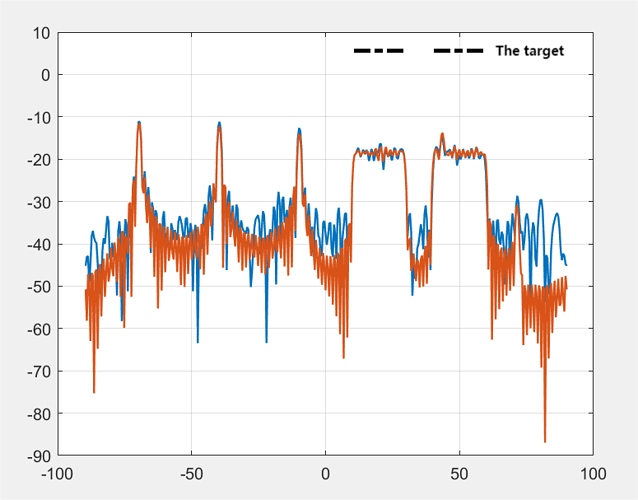
Thanks for reply.I’m sorry for the inconvenience.But my problem is still there, from my final results, CVX does not give a satisfactory solution, the objective function is not minimized.I iterate many times(>1000) is still not close to the target. The figure below shows the result after ten iterations.
Perhaps it is the paper’s algorithm which is deficient, not “CVX”. I warned you that it might not converge to anything, let alone the right thing.
Thank you. I’ll check the algorithm again.It really gets me down.
By the way, why does converting norm(f) <= sqrt(Pt) to a first-order form improve the stability of a single solution, and does that apply to all second-order problems
The norm() is a nicer function that behaves like a linear function e.g
norm(a*x) = |a|*norm(x)
whereas
norm(ax)^2 = |a|^2norm(x)^2
behaves like the quadratic function it is.
Also the number
sqrt(Pt)
is closer to 1 than
Pt
which makes your model better scaled.
What is your argument that a squared norm is better than the norm?