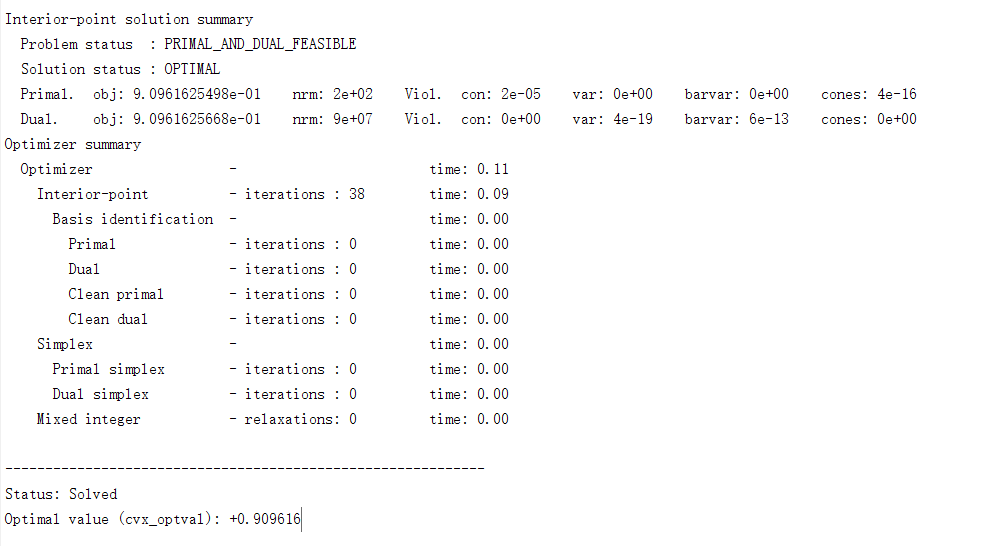
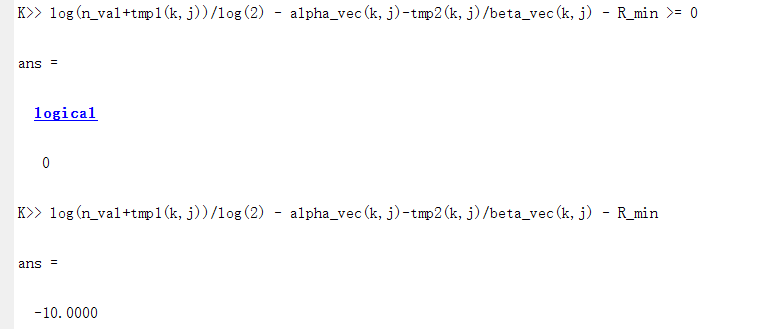The solution of CVX can’t satisfy the constraint. The optimal Status is solved, but when I check the results, the constraint is not satisfied, which is shown in the following picture. Here, the tmp1(k,j) and tmp2(k,j) is the cvx real affine expression, and other element in these constraint is constant.
Only variable values are populated by CVX after optimization. Expressions are just placeholders and using them outside of CVX context will give you arbitrary rubbish. To compute their values you have to go back to the CVX variables and compute with those.
I use the variable values to check the cosntraint, but it’s still not satisfied
Please provide a fully reproducible example that can be copied and executed.
function [rate_tmp,W_tmp,S_tmp] = ISAC_sub3(h_matr,n_val,ar,at,B,Sm,R_min,tau_min,alpha_vec,beta_vec,Nt,Nr,W_bfrc,Omega_bfrc,num_ue,num_tar)
cvx_clear
cvx_begin sdp
cvx_solver mosek
variable W(Nt,Nt,num_ue) hermitian semidefinite
variable S(Nt,Nt) hermitian semidefinite
expressions tmp1(num_ue,num_ue) tmp2(num_ue,num_ue) Tm(num_tar) Omega(Nr,Nr,num_tar) Xstar(num_tar) Ck(10);
obj_sub = trace(S);
for ss = 1:num_ue
obj_sub = obj_sub + trace(W(:,:,ss));
end
minimize(real(obj_sub));
for k = 1:num_ue
for j = k:num_ue
for i = k:num_ue
tmp1(k,j) = tmp1(k,j) + real(trace(h_matr(:,j)*h_matr(:,j)‘W(:,:,i)));
if i>k
tmp2(k,j) = tmp2(k,j)+real(trace(h_matr(:,j)h_matr(:,j)'(W(:,:,i)-W_bfrc(:,:,i))));
end
end
end
end
Xstar = sum(W,3) + S;
for m = 1:num_tar
Omega(:,:,m) = Sm(:,:,m) * Xstar(m) * Sm(:,:,m)’ + n_valeye(Nr);
Tm(m) = ar(:,m)’ * inv(Omega_bfrc(:,:,m)) * ar(:,m) - ar(:,m)’ * inv(Omega_bfrc(:,:,m)) * (Omega(:,:,m) - Omega_bfrc(:,:,m)) * inv(Omega_bfrc(:,:,m)) * ar(:,m);
end
subject to
for mm = 1:num_tar
real(Tm(mm))* B(mm) - tau_min*inv_pos(at(:,mm)'*Xstar*at(:,mm)) >= 0
end
subject to
for k = 1:num_ue
for j = k:num_ue
beta_vec(k,j) * log(n_val+tmp1(k,j))/log(2) - beta_vec(k,j) * alpha_vec(k,j)-tmp2(k,j)- beta_vec(k,j) * R_min >= 0
end
end
cvx_end
% get result
W_tmp = zeros(Nt,Nt,num_ue);
for kk = 1:num_ue
W_tmp(:,:,kk) = (h_matr(:,kk)'*W(:,:,kk)*h_matr(:,kk))^(-1)*W(:,:,kk)*h_matr(:,kk)*h_matr(:,kk)'*W(:,:,kk)';
end
S_tmp = sum(W,3) + S - sum(W_tmp,3);
rate_tmp = cvx_optval;
end
n_val = 5.0119e-12, Nr = Nt = 8, R_min = tau_min = 10, num_ue = 4, num_tar = 2
and
h_matr =
1.0e-03 *
0.0028 + 0.0000i 0.0082 + 0.0000i 0.0379 + 0.0000i 0.5129 + 0.0000i
-0.0026 - 0.0011i 0.0000 - 0.0082i 0.0000 + 0.0379i -0.4681 + 0.2095i
0.0019 + 0.0021i -0.0082 - 0.0000i -0.0379 + 0.0000i 0.3416 - 0.3825i
-0.0008 - 0.0027i -0.0000 + 0.0082i -0.0000 - 0.0379i -0.1555 + 0.4887i
-0.0003 + 0.0028i 0.0082 + 0.0000i 0.0379 - 0.0000i -0.0577 - 0.5096i
0.0014 - 0.0024i 0.0000 - 0.0082i 0.0000 + 0.0379i 0.2609 + 0.4415i
-0.0023 + 0.0016i -0.0082 - 0.0000i -0.0379 + 0.0000i -0.4185 - 0.2964i
0.0027 - 0.0005i -0.0000 + 0.0082i -0.0000 - 0.0379i 0.5031 + 0.0995i
B =
1.0e-10 *
0.3981
0.3981
ar = at =
1.0000 + 0.0000i 1.0000 + 0.0000i
-0.4337 - 0.9011i -0.4337 + 0.9011i
-0.6238 + 0.7816i -0.6238 - 0.7816i
0.9748 + 0.2232i 0.9748 - 0.2232i
-0.2217 - 0.9751i -0.2217 + 0.9751i
-0.7825 + 0.6226i -0.7825 - 0.6226i
0.9004 + 0.4351i 0.9004 - 0.4351i
0.0015 - 1.0000i 0.0015 + 1.0000i
Omega_bfrc(:,:,1) =
1.0e-11 *
0.5012 + 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 - 0.0000i
-0.0000 + 0.0000i 0.5012 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i
-0.0000 - 0.0000i -0.0000 + 0.0000i 0.5012 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i
0.0000 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.5012 + 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i -0.0000 - 0.0000i
-0.0000 + 0.0000i 0.0000 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.5012 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 + 0.0000i
-0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.5012 + 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i
0.0000 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.5012 + 0.0000i -0.0000 - 0.0000i
0.0000 + 0.0000i 0.0000 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.0000 - 0.0000i -0.0000 - 0.0000i -0.0000 + 0.0000i 0.5012 + 0.0000i
Omega_bfrc(:,:,2) =
1.0e-11 *
0.5012 - 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 - 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 - 0.0000i 0.0000 + 0.0000i
-0.0000 - 0.0000i 0.5012 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 - 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 - 0.0000i
-0.0000 + 0.0000i -0.0000 - 0.0000i 0.5012 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 - 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i
0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.5012 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 - 0.0000i -0.0000 + 0.0000i
-0.0000 - 0.0000i 0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.5012 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 - 0.0000i
-0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.5012 - 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i
0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.5012 - 0.0000i -0.0000 + 0.0000i
0.0000 - 0.0000i 0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.0000 + 0.0000i -0.0000 + 0.0000i -0.0000 - 0.0000i 0.5012 + 0.0000i
W_bfrc = ones(Nt,Nt,num_ue)
Thanks for replying, it’s a simple sample for my optimal problem.
Could you make it easier for us by showing explicitly a constraint which is not satisfied, and your calculation which shows that? Keep in mind that CVX and the solver it calls allow constraints to be violated to within a feasibility tolerance. So if the constraint is LHS >= 0, LHS might wind up being -1e-8 in the optimal solution, and that constraint is considered to not be violated.