"The second argument must be positive or negative semidefinite" but it is

1

Hi all,

I’m tackling the following nonconvex fractional quadratic optimization problem

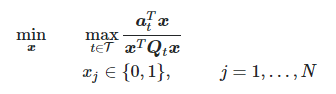
image

where \boldsymbol{x}=[x_1,\dots,x_N]^T, \boldsymbol{a}_t = [a_{1t},\dots,a_{Nt}]^T\, \forall t \in \mathcal{T} and \boldsymbol{Q}_t \in \mathbb{R}_+^{N \times N} \, \forall t \in \mathcal{T} is a stricly lower triangular matrix.

After relaxing the binary constraint, my idea is to use the bisection method being the problem quasi-convex, i.e. I’d check the problem feasibility for smaller and smaller values of a constant z until the problem becomes infeasible. Below is one iteration of the method.

cvx_begin
variable x(N,1)
subject to
for t = 1:T
a_t = A_all(t,:)’;
Q_t = triu(reshape(Q_all(t,:,:),N,N));
a_t’*x <= z * x’*Q_t’*x;
end
0<=x<=1
cvx_end

Unfortunately, CVX returns the error “The second argument must be positive or negative semidefinite”, even though matrix \boldsymbol{Q}_t is positive semidefinite for all t. I also tested it by means of the MATLAB eig function, which gives N zero eigenvalues.

At first I thought it was some kind of numerical problem, so I scaled up the input data. Currently, \boldsymbol{Q}_t's are in the order of 10^3, while \boldsymbol{a}_t's are in the order of 10^2 and I wouldn’t expect it to be an issue for the solver.

Do you have any suggestions? Thank you.

2

For the inequality a_t’*x <= z * x’*Q_t’*x; to be convex Q must be negative semidefinite (assuming z is positive)

3

Thank you, I missed that. Shouldn’t it work anyway since all \boldsymbol{Q}_t's eigenvalues are zero? Yes, z is positive.

4

And I missed that Q is not symmetric. The correct statement then would be that the symmetrization of Q must be NSD.

2 Likes
5

The symmetrization is not NSD, indeed. I can’t see why you would need to enforce this though. Could you point me to a reference on the matter? Thank you.

6

If the symmetrizationof Q is not NDS, then the constraint is non-convex, and can’t be handled in CVX. if you have a proof otherwise, and are under 40, you could be in line for the Fields Medal.

1 Like