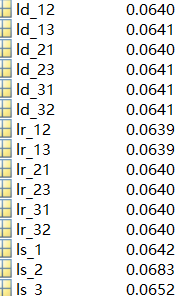
Hello everyone, thank you in advance for your help. I use cvx to optimize several variables. In the objective function, the formula in which some optimization variables are located is multiplied by 0, but their optimization results are not 0, or even large. May I ask why this situation occurs? And cvx often fails to solve, but I checked that my objective function and constraints are convex, hoping to help me find the problem, thank you very much.Here’s my code.
% Include CVX and set the solver to Mosek
% addpath('/path/to/cvx');
% cvx_setup;
% clear all;
cvx_solver mosek;
% Clear CVX environment
cvx_clear;
% Define problem data
C = 64; % Quantization bits
q = 64;
V = 0.5; % Lyapunov weight
alpha = 1;
Round_num = 1000; % Total rounds of training
Device_num = 3; % Number of devices
Date_num = 128 * ones(1, Device_num); % Data amount for each device
d_c = 0.1; % Compute resource requirement
M = 878538;
% Power definitions
% Generate a vector of random numbers following a normal distribution
mu = 0;
sigma = 1;
rand_nums = mu + sigma * randn(1, Device_num);
% Standardize the random number vector
rand_nums = (rand_nums - mean(rand_nums)) / max(abs(rand_nums)) * 1;
% Compute Power_s
Power_s = 1.0 * ones(1, Device_num) - 0.05 * rand_nums;
% Compute Power_ijD
Power_ijD = 1.0 * ones(Device_num, Device_num) - 0.05 * rand_nums;
% Compute Power_jir
Power_jir = 1.0 * ones(Device_num, Device_num) - 0.05 * rand_nums;
a = zeros(Device_num);
b = ones(1, Device_num);
%b(1) = 0;
%a(1,2) = 1;
Frequency = 1.5 * ones(1, Device_num) - 0.1 * rand_nums;
Band = 2e7;
Min_bandwidth = 0.1 / Device_num;
N0 = dBm_to_P(-174) * Band;
% Compute channel gain from users to the base station
H_i = zeros(1, Device_num);
d = 1; % Distance in kilometers
% Randomly distribute devices
base_station = [0, 0];
% Generate random user coordinates
Device_num = 3;
theta = 2 * pi * rand(1, Device_num);
radius = 200 * rand(1, Device_num);
% Convert polar coordinates to Cartesian coordinates
users_x = base_station(1) + radius .* cos(theta);
users_y = base_station(2) + radius .* sin(theta);
users_coordinates = [users_x; users_y];
% Calculate the distance from each device to the base station
Distance_i = sqrt((users_coordinates(1, :) - base_station(1)).^2 + ...
(users_coordinates(2, :) - base_station(2)).^2);
% Calculate the distance between devices
Distance_ij = zeros(Device_num, Device_num);
for i = 1:Device_num
for j = 1:Device_num
Distance_ij(i, j) = sqrt((users_coordinates(1, i) - users_coordinates(1, j)).^2 + ...
(users_coordinates(2, i) - users_coordinates(2, j)).^2);
end
end
% Compute channel gain from users to the base station
for k = 1:Device_num
H_i(k) = channel_gain(Distance_i(k));
end
% Compute channel gain between users
H_ij = zeros(Device_num, Device_num);
for i = 1:Device_num
for j = 1:Device_num
H_ij(i, j) = channel_gain(Distance_ij(i, j));
end
end
T_total = [];
D2D_total = [];
E_final = [];
D2D_energy_total = [];
t_D2D = 0;
Energy_coefficient = 0.1; % Energy efficiency
n_iterations = 20;
a12 = 0;
a21 = 0;
a13 = 0;
a31 = 0;
a23 = 0;
a32 = 0;
b1 = 1;
b2 = 1;
b3 = 1;
% for iteration = 1:n_iterations
% Define CVX variables
cvx_begin
variable ls_1
variable ls_2
variable ls_3
variable ld_12
variable ld_21
variable ld_13
variable ld_31
variable ld_23
variable ld_32
variable lr_12
variable lr_21
variable lr_13
variable lr_31
variable lr_23
variable lr_32
variable T
expression t1_s
expression t1_D2D
expression t1
expression t2_s
expression t2_D2D
expression t2
expression t3_s
expression t3
% Three devices
% Device 1 delay
% Direct upload to the base station delay
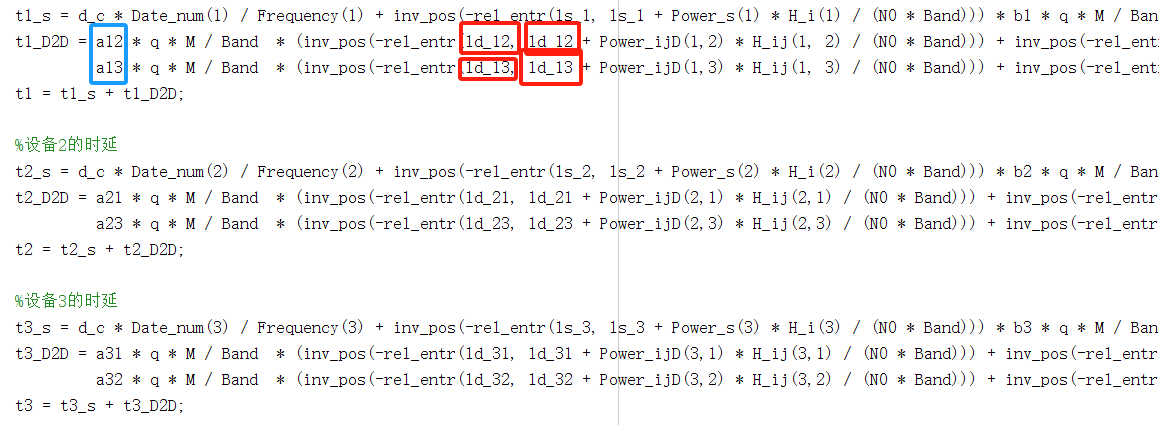
t1_s = d_c * Date_num(1) / Frequency(1) + inv_pos(-rel_entr(ls_1, ls_1 + Power_s(1) * H_i(1) / (N0 * Band))) * b1 * q * M / Band;
t1_D2D = a12 * q * M / Band * (inv_pos(-rel_entr(ld_12, ld_12 + Power_ijD(1,2) * H_ij(1, 2) / (N0 * Band))) + inv_pos(-rel_entr(lr_21, lr_21 + Power_jir(2, 1) * H_i(2) / (N0 * Band)))) + ...
a13 * q * M / Band * (inv_pos(-rel_entr(ld_13, ld_13 + Power_ijD(1,3) * H_ij(1, 3) / (N0 * Band))) + inv_pos(-rel_entr(lr_31, lr_31 + Power_jir(3, 1) * H_i(3) / (N0 * Band))));
t1 = t1_s + t1_D2D;
% Device 2 delay
t2_s = d_c * Date_num(2) / Frequency(2) + inv_pos(-rel_entr(ls_2, ls_2 + Power_s(2) * H_i(2) / (N0 * Band))) * b2 * q * M / Band;
t2_D2D = a21 * q * M / Band * (inv_pos(-rel_entr(ld_21, ld_21 + Power_ijD(2,1) * H_ij(2,1) / (N0 * Band))) + inv_pos(-rel_entr(lr_12, lr_12 + Power_jir(1,2) * H_i(1) / (N0 * Band)))) + ...
a23 * q * M / Band * (inv_pos(-rel_entr(ld_23, ld_23 + Power_ijD(2,3) * H_ij(2,3) / (N0 * Band))) + inv_pos(-rel_entr(lr_32, lr_32 + Power_jir(3, 2) * H_i(3) / (N0 * Band))));
t2 = t2_s + t2_D2D;
% Device 3 delay
t3_s = d_c * Date_num(3) / Frequency(3) + inv_pos(-rel_entr(ls_3, ls_3 + Power_s(3) * H_i(3) / (N0 * Band))) * b3 * q * M / Band;
t3_D2D = a31 * q * M / Band * (inv_pos(-rel_entr(ld_31, ld_31 + Power_ijD(3,1) * H_ij(3,1) / (N0 * Band))) + inv_pos(-rel_entr(lr_13, lr_13 + Power_jir(1,3) * H_i(1) / (N0 * Band)))) + ...
a32 * q * M / Band * (inv_pos(-rel_entr(ld_32, ld_32 + Power_ijD(3,2) * H_ij(3,2) / (N0 * Band))) + inv_pos(-rel_entr(lr_23, lr_23 + Power_jir(2, 3) * H_i(2) / (N0 * Band))));
t3 = t3_s + t3_D2D;
minimize(T);
% Add constraints
subject to
ls_1 >= 0
ls_2 >= 0
ls_3 >= 0
ld_12 >= 0
ld_21 >= 0
ld_13 >= 0
ld_31 >= 0
ld_23 >= 0
ld_32 >= 0
lr_12 >= 0
lr_21 >= 0
lr_13 >= 0
lr_31 >= 0
lr_23 >= 0
lr_32 >= 0
ls_1 + ls_2 + ls_3 + ld_12 + ld_21 + ld_31 + ld_23 + ld_13 + ld_32 + lr_12 + lr_21 + lr_13 + lr_31 + lr_23 + lr_32 <= 1
T >= t1
T >= t2
T >= t3
cvx_end
% Second optimization problem
% end
% Display results
disp(['Minimized objective function value: ' num2str(T)]);
% Power_s(1)
% H_i(1)
% (N0 * Band)
% k = Power_s(1) * H_i(1) / (N0 * Band)
% Compute gain
function gain = channel_gain(d)
% Calculate gain based on distance
rng('shuffle');
gain = 10 ^ ((-128.1 - 37.6 * log10(d / 1000)) / 10 - raylrnd(0.1));
end
function p = dBm_to_P(b)
p = 10 ^ ((b - 30) / 10);
end
% Generate random distances
function Distance_ij = generateDistanceMatrix(n)
Distance_ij = zeros(n, n);
for i = 1:n
for j = i+1:n
distance = randi([1, 200]);
Distance_ij(i, j) = distance;
Distance_ij(j, i) = distance;
end
end
end