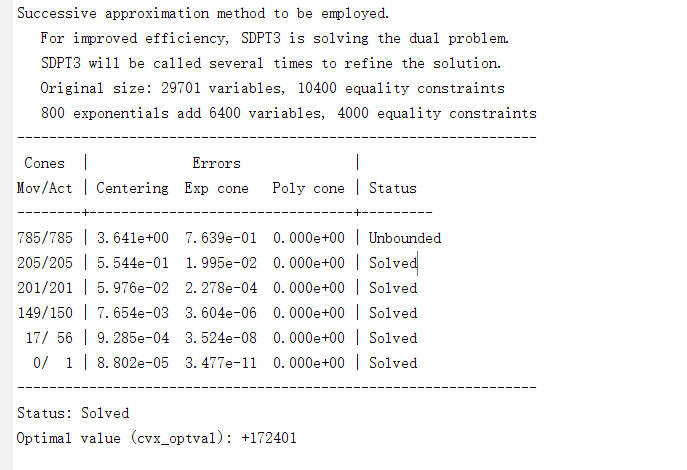
Hello, I encountered a very strange problem when using the CVX toolbox. cvx_optval is not equal to the object value of the optimized variable value obtained using CVX.
My matlab code is as follows:

disp(counter)
disp(’%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%’)
cvx_begin
% cvx_quiet(true)
variable q_opt(6,N+1);
variable y(2,N) nonnegative;
variable R_opt(KM,N) nonnegative
variable z_opt(KM,N) nonnegative
variable l_km(K*M,N) nonnegative
variable l_mm(M,N) nonnegative
minimize UAV_P0*sum(T+3/UAV_Utip/UAV_Utip.*pow_pos(norms(q_opt(1:3,2:N+1)-q_opt(1:3,1:N)),2).*inv_pos(T))+UAV_Pi*sum(y(1,:))+1/2*d0*UAV_ruo*UAV_A*UAV_s*sum(pow_pos(norms(q_opt(1:3,2:N+1)-q_opt(1:3,1:N)),3).*pow_pos(inv_pos(T),2))+UAV_P0*sum(T+3/UAV_Utip/UAV_Utip.*pow_pos(norms(q_opt(4:6,2:N+1)-q_opt(4:6,1:N)),2).*inv_pos(T))+UAV_Pi*sum(y(2,:))+1/2*d0*UAV_ruo*UAV_A*UAV_s*sum(pow_pos(norms(q_opt(4:6,2:N+1)-q_opt(4:6,1:N)),3).*pow_pos(inv_pos(T),2))+G*sum(sum(pow_pos(l_mm,3)).*pow_pos(inv_pos(T),2))
subject to
l_km(:,1)==0;
l_km>=0;
l_mm>=0;
for m=1:M
for n=1:N
l_mm(m,n)<=f_hmax*T(1,n); %小于无人机的最大计算频率
end
end
for n=1:N
l_km(1:2:2*K,n) + l_km(2:2:2*K,n)<=f_kmax*T(1,n);
end
for m=1:M
sum(l_mm(m,:))+sum(sum(l_km(m:2:2*K,:)))>=Q;
end
for k=1:K
for m=1:M
for n=1:N
z_opt((k-1)*M+m,n)<=pow_pos(norm(qmr(3*(m-1)+1:3*m,n+1) - pos(:,k)),2)+...
2*(qmr(3*(m-1)+1:3*m,n+1) - pos(:,k))'*(q_opt(3*(m-1)+1:3*m,n+1) - qmr(3*(m-1)+1:3*m,n+1));
end
end
end
z_opt>=0;
for k=1:K
for m=1:M
for n=1:N
if m==1
R_opt((k-1)M+m,n)<=R1_1((k-1)M+m,n)-R1_2((k-1)M+m,n).(pow_pos(norm(q_opt(3(m-1)+1:3m,n+1) - pos(:,k)),2)-pow_pos(norm(qmr(3*(m-1)+1:3m,n+1) - pos(:,k)),2))-temp_1+log(1-temp_2inv_pos(z_opt((k-1)M+2,n)+temp_2))/log(2);
else
R_opt((k-1)M+m,n)<=R1_1((k-1)M+m,n)-R1_2((k-1)M+m,n).(pow_pos(norm(q_opt(3(m-1)+1:3m,n+1) - pos(:,k)),2)-pow_pos(norm(qmr(3(m-1)+1:3m,n+1) - pos(:,k)),2))-temp_1+log(1-temp_2inv_pos(z_opt((k-1)*M+1,n)+temp_2))/log(2);
end
end
end
end
R_opt>=0;
for k=1:K
for m=1:M
for n=1:N-1
T(1,n)*d_km_inta((k-1)*M+m,n)*R_opt((k-1)*M+m,n)==l_km((k-1)*M+m,n+1);
end
end
end
%2
for m=1:M
for n=1:N
square_pos(quad_over_lin(T(n),y(m,n)))<=(y_initial(m,n)^2+2*y_initial(m,n)*(y(m,n)-y_initial(m,n))-pow_pos(norms(qmr((m-1)*3+1:3*m,n+1)-qmr((m-1)*3+1:3*m,n)),2)/UAV_v0^2+2/UAV_v0^2*(qmr((m-1)*3+1:3*m,n+1)-qmr((m-1)*3+1:3*m,n))'*(q_opt((m-1)*3+1:3*m,n+1)-q_opt((m-1)*3+1:3*m,n)));
end
end
%4
y>=0;
%3
q_opt(1:2,1) == q_0;
q_opt(1:2,N+1)== q_F;
q_opt(4:5,1)==q_0;
q_opt(4:5,N+1)==q_F;
q_opt(3,1)==120;
q_opt(3,N+1)==120;
q_opt(6,1)==130;
q_opt(6,N+1)==130;
for m=1:M
for n=2:N
q_opt(3,n)>=100;
q_opt(3,n)<=150;
q_opt(6,n)>=100;
q_opt(6,n)<=150;
end
end
for n=1:N
norm(q_opt(1:2,n+1)-q_opt(1:2,n))<=T(:,n)*V_max;
norm(q_opt(4:5,n+1)-q_opt(4:5,n))<=T(:,n)*V_max;
norm(q_opt(3,n+1)-q_opt(3,n))<=T(:,n)*20;
norm(q_opt(6,n+1)-q_opt(6,n))<=T(:,n)*20;
end
for n=1:N
norm(q_opt(1:3,n+1)-q_opt(1:3,n))<=20;
norm(q_opt(4:6,n+1)-q_opt(4:6,n))<=20;
end
for n=1:N+1
2*(qmr(1:3,n) - qmr(4:6,n))'*(q_opt(1:3,n) - q_opt(4:6,n))-pow_pos(norm(qmr(1:3,n) - qmr(4:6,n)),2)>=10^2;
end
cvx_end
val3 = cvx_optval;
qmr = q_opt;
Lm = l_mm;
Lk = l_km;
y_initial = y;
enger_counter_3(1,counter)=UAV_P0sum(T+3/UAV_Utip/UAV_Utip.pow_pos(norms(q_opt(1:3,2:N+1)-q_opt(1:3,1:N)),2).inv_pos(T))+UAV_Pisum(y(1,:))+1/2d0UAV_ruoUAV_AUAV_ssum(pow_pos(norms(q_opt(1:3,2:N+1)-q_opt(1:3,1:N)),3).pow_pos(inv_pos(T),2))+UAV_P0sum(T+3/UAV_Utip/UAV_Utip.pow_pos(norms(q_opt(4:6,2:N+1)-q_opt(4:6,1:N)),2).inv_pos(T))+UAV_Pisum(y(2,:))+1/2d0UAV_ruoUAV_AUAV_s*sum(pow_pos(norms(q_opt(4:6,2:N+1)-q_opt(4:6,1:N)),3).pow_pos(inv_pos(T),2))+Gsum(sum(pow_pos(l_mm,3)).*pow_pos(inv_pos(T),2));