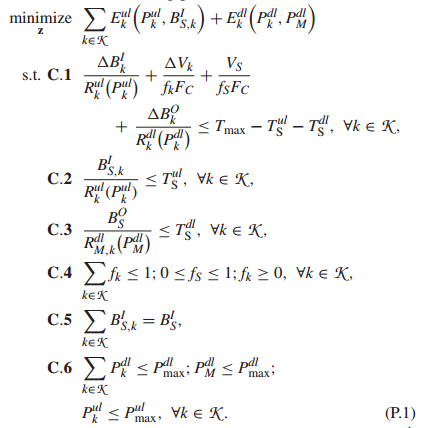Dear everyone,
I meet some problems when I use CVX.
My version of cvx: 2.1.
The error I met is followed:
CVX Warning:
Models involving “log” or other functions in the log, exp, and entropy
family are solved using an experimental successive approximation method.
This method is slower and less reliable than the method CVX employs for
other models. Please see the section of the user’s guide entitled
The successive approximation method
for more details about the approach, and for instructions on how to
suppress this warning message in the future.
警告: The use of strict inequalities in CVX is strongly discouraged,
because solvers treat them as non-strict inequalities. Please
consider using “>=” instead.
In > (line 21)
In cvx_test4 (line 221)
警告: The use of strict inequalities in CVX is strongly discouraged,
because solvers treat them as non-strict inequalities. Please
consider using “>=” instead.
In > (line 21)
In cvx_test4 (line 222)
警告: The use of strict inequalities in CVX is strongly discouraged,
because solvers treat them as non-strict inequalities. Please
consider using “>=” instead.
In > (line 21)
In cvx_test4 (line 223)
Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 533 variables, 222 equality constraints
24 exponentials add 192 variables, 120 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
7/ 7 | 6.435e+00 5.254e-01 0.000e+00 | Inaccurate/Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Inaccurate/Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Infeasible
Status: Unbounded
Optimal value (cvx_optval): -Inf
My code is followed:
clc; clear all;
k = 8; % The number of user in a small cell
%PL = 0;pk.*hk.^2/(B*N0)
PL=0;
% rayleigh fading
Fs = 9600;
Ts = 1/Fs;
fdmax = 0;
Delay=1e-6*[10.15];
PowerdB=-2*ones(1,1);
rayCh = rayleighchan(Ts,fdmax,Delay,PowerdB);
r = abs(rayCh.PathGains);
for i = 2:k
rayCh = rayleighchan(Ts,fdmax,Delay,PowerdB);
r = [r,abs(rayCh.PathGains)]; % The uplink and downlink channel power gains of user k
end
energy=0;
for n=0.1:0.1:1
%Simulation parameters
N0 = 1e-10; % noise power spectral density(W/Hz)
Wul = 1e8; Wdl = 1e8; % The uplink and downlink bandwidth (Hz)
Pumax = 0.25; Pdmax = 20; %0.1 100 %0.25 20 % The uplink and downlink power(w)
FC = 10^12; % The cloudlet server processing capacity(CPU cycles/s)
luk = 1.78*10^-6; % The amount of energy spent by the mobile device to extract each bit of offloaded data from the video source(J/bit)
ldk = 0.625; % Parameter that captures the mobile receiving energy expenditure per second in the downlink(J/s)
BIk = 1e6*ones(1,k); %1e4 % Input bits from each user k to the cloudlet in the uplink (1Mbits)
BIs = n*BIk; % Shared input bits that can be sent by any of the users
BOk = 1e6*ones(1,k); % Out bits from the cloudlet to each user k in the downlink (1Mbits)
BOs = n*BOk; % Shared output bits that delivered to all users
Vk = 1000*BIk; % Processing the input BIk by executing Vk CPU cycles at the cloudlet (CPU cycles)
Vs = n*Vk; % Shared CPU cycles
Tmax = 1; %0.3 % Maximum latency constraint(0.15s/0.05s)
%Initialize the z = [Pul,Bls,f,Pdl,PdM,TuS,TdS]
Pulk0 = Pumax*rand(1,k); % The uplink power(w)of user k
%Pdlk0 = Pdmax/k*ones(1,k); % The downlink power(w)to user k
Pdlk0 = rand(1,k);
Pdlk0 = Pdlk0/(sum(Pdlk0))*Pdmax;
%PdlkI = Pdmax*rand(1,k);
PdlM0 = Pdmax*rand(1,1); % Transmit power (w) for multicasting
%BIsk0 = BIs/k.*ones(1,k); % A fraction of BIsk bits of the BIs shared bits transmited by user k
BIsk0 = rand(1,k);
BIsk0 = BIsk0/(sum(BIsk0)).*BIs;
fk0 = rand(1,k);
fk0 = fk0/(sum(fk0))*1;
fs0 = rand(1,1); % Fractions of the processing power FC assigned to run the Vk CPU cycles exclusively for user k and the VS shared CPU cycles
f0 = [fk0,fs0];
PU0 = r.*(Pulk0-PL);
Rulk0 = (Wul/k)*log2(1+PU0/(N0*Wul/k));
PD0 = r.*(Pdlk0-PL); % The downlink power after rayleigh fading
Rdlk0 = (Wdl/k)*log2(1+PD0/(N0*Wdl/k));
PM0 = r.*(PdlM0-PL); % Multicasting power after rayleigh fading
RdlMk0 = Wdl*log2(1+PM0/(N0*Wdl)); % Transmitting rate to users for multicasting
TuS0 = max(BIsk0./Rulk0); % The time to complete the shared uplink transmissions (s)
TdS0 = max(BOs./RdlMk0); % The downlink transmission time to multicast BOs bits
T = max((BIk - BIs + BIsk0)./(Rulk0)+(Vk-Vs)/(FC.*fk0)+Vs/(FC*fs0)+(BOk-BOs)./(Rdlk0)+max(BIsk0./Rulk0)+max(BOs./(RdlMk0)))
z0 = [Pulk0,BIsk0,f0,Pdlk0,PdlM0,TuS0,TdS0];
Eulk = (Pulk0./Rulk0+luk).*(BIk-BIs+BIsk0);
Edlk = ((BOk-BOs)./Rdlk0+BOs./RdlMk0)*ldk;
Eneval0 = sum(Eulk+Edlk);
% Accuracy parameters
alpha = 10^-5; epsilong = 10^-8; delta0 = rand;
%z = zeros(1,4*k+4); acc = norm(z-z0,2)^2;
Eneval = 0; acc = norm(Eneval-Eneval0,2)^2;
v = 0; accu = 0; value = 0;
while acc > epsilong
cvx_begin
%cvx_solver ecos
%cvx_solver mosek
%cvx_solver SeDuMi
variables Pulk(1,k) BIsk(1,k) fk(1,k) fs Pdlk(1,k) PdlM TuS TdS;
f = [fk,fs];
z = [Pulk,BIsk,f,Pdlk,PdlM,TuS,TdS];
PU = r.*Pulk;
Rulk = (Wul/k)*log(1+PU/(N0*Wul/k))/log(2);
PD = r.*Pdlk;
Rdlk = (Wdl/k)*log(1+PD/(N0*Wdl/k))/log(2);
PM = r.*PdlM;
RdlMk = Wdl*log(1+PM/(N0*Wdl))/log(2);
% The overall downlink mobile energy consumption for user k
Edlk = ((BOk-BOs).*inv_pos(Rdlk)+(BOs.*inv_pos(RdlMk)))*ldk;
% Mobile energy consumption of uplink transmission
% E = (z-z0)*diag(z0)*(z-z0)';
e1 = Pulk0.*(BIk-BIs+BIsk0).*inv_pos(Rulk);
e2 = Pulk0.*(BIk-BIs+BIsk)./Rulk0;
e3 = Pulk.*(BIk-BIs+BIsk0)./Rulk0;
e4 = luk*(BIk-BIs+BIsk);
Eulk = e1+e2+e3+(z-z0)*diag(z0)*(z-z0)'+e4;
% Rewrite the latency constraints C.2
g1 = square_pos(BIsk+inv_pos(Rulk));
g2 = Rulk0.*Rulk0;
g3 = (g1-BIsk0.^2-1./g2);
g4 = BIsk0.*(BIsk-BIsk0);
g5 = (r.*Pulk0)/(N0*Wul/k);
g6 = (1+g5).*(Rulk0.^4);
g7 = g4-(Rulk0./g6).*(inv_pos(Rulk)-1./Rulk0);
gk = 1/2*g3-g7;
minimize(sum(Eulk+Edlk))
subject to
(BIk - BIs + BIsk0).*inv_pos(Rulk)+(Vk-Vs)/FC.*inv_pos(fk)+Vs/FC*inv_pos(fs)+(BOk-BOs).*inv_pos(Rdlk) +TuS+TdS<= Tmax; % Constraint C.1
% gk <= 0.01;
% (BOs.*inv_pos(RdlMk))<=1e-3;
gk-TuS <= 0; % Constraint C.2
(BOs.*inv_pos(RdlMk))-TdS <= 0; % Constraint C.3
TuS+TdS <= Tmax;
TuS >= 0;
TdS >= 0;
TuS <= 0.2;
TdS <= 0.02;
sum(fk) <= 1; % Constraint C.4
fk <= 1;
fs <= 1;
fk >= 0;
fs >= 0;
sum(BIsk) == BIs; % Constraint C.5
sum(Pdlk) <= Pdmax; % Constraint C.6
Pdlk <= Pdmax;
PdlM <= Pdmax;
Pulk <= Pumax;
Pdlk > 1e-3;
PdlM > 1e-3;
Pulk > 1e-3;
BIsk <= BIs;
BIsk >= 0;
cvx_end
v = v+1
T = max((BIk - BIs + BIsk)./(Rulk)+(Vk-Vs)/(FC.*fk)+Vs/(FC*fs)+(BOk-BOs)./(Rdlk)+max(BIsk./Rulk)+max(BOs./(RdlMk)))
if (T<=Tmax)&&(z(1)>0.01)
Rulk = Wul/k*log2(1+r.*Pulk/(N0*Wul/k));
Eulk = (Pulk./Rulk+luk).*(BIk-BIs+BIsk);
% e1 = Pulk0.*(BIsk0+(BIk-BIsk0))./Rulk;
% e2 = Pulk0.*(BIsk+(BIk-BIsk0))./Rulk0;
% e3 = Pulk.*(BIsk0+(BIk-BIsk0))./Rulk0;
% e4 = luk*(BIsk+(BIk-BIsk0));
% Eulk = e1+e2+e3+(z-z0)*diag(z0)*(z-z0)'+e4;
Rdlk = Wdl/k*log2(1+r.*Pdlk/(N0*Wdl/k));
RdlMk = Wdl*log2(1+r.*PdlM/(N0*Wul));
Edlk = ((BOk-BOs)./Rdlk+BOs./RdlMk)*ldk;
Eneval = sum(Edlk+Eulk);
value = [value,Eneval];
acc = norm(Eneval-Eneval0,2)^2
accu = [accu,acc];
z0 = z0+delta0*(z-z0);
delta0 = delta0*(1-alpha*delta0);
Pulk0 = z0(1:k); BIsk0 = z0(k+1:k+k); fk0 = z0(2*k+1:3*k); fs0 = z0(3*k+1);
Pdlk0 = z0(3*k+2:4*k+1); PdlM0 = z0(4*k+2); TuS0 = z0(4*k+3); TdS0 = z0(4*k+4);
Eneval0 = Eneval;
else
%Initialize the z = [Pul,Bls,f,Pdl,PdM,TuS,TdS]
Pulk0 = Pumax*rand(1,k); % The uplink power(w)of user k
%Pdlk0 = Pdmax/k*ones(1,k); % The downlink power(w)to user k
Pdlk0 = rand(1,k);
Pdlk0 = Pdlk0/(sum(Pdlk0))*Pdmax;
%PdlkI = Pdmax*rand(1,k);
PdlM0 = Pdmax*rand(1,1); % Transmit power (w) for multicasting
%BIsk0 = BIs/k.*ones(1,k); % A fraction of BIsk bits of the BIs shared bits transmited by user k
BIsk0 = rand(1,k);
BIsk0 = BIsk0/(sum(BIsk0)).*BIs;
fk0 = rand(1,k);
fk0 = fk0/(sum(fk0))*1;
fs0 = rand(1,1); % Fractions of the processing power FC assigned to run the Vk CPU cycles exclusively for user k and the VS shared CPU cycles
f0 = [fk0,fs0];
PU0 = r.*(Pulk0-PL);
Rulk0 = (Wul/k)*log2(1+PU0/(N0*Wul/k));
PD0 = r.*(Pdlk0-PL); % The downlink power after rayleigh fading
Rdlk0 = (Wdl/k)*log2(1+PD0/(N0*Wdl/k));
PM0 = r.*(PdlM0-PL); % Multicasting power after rayleigh fading
RdlMk0 = Wdl*log2(1+PM0/(N0*Wdl)); % Transmitting rate to users for multicasting
TuS0 = max(BIsk0./Rulk0); % The time to complete the shared uplink transmissions (s)
TdS0 = max(BOs./RdlMk0); % The downlink transmission time to multicast BOs bits
% TuS = 1e-2;TdS = 1e-3;
T = max((BIk - BIs + BIsk0)./(Rulk0)+(Vk-Vs)/(FC.*fk0)+Vs/(FC*fs0)+(BOk-BOs)./(Rdlk0)+max(BIsk0./Rulk0)+max(BOs./(RdlMk0)))
z0 = [Pulk0,BIsk0,f0,Pdlk0,PdlM0,TuS0,TdS0];
Eulk = (Pulk0./Rulk0+luk).*(BIk-BIs+BIsk0);
Edlk = ((BOk-BOs)./Rdlk0+BOs./RdlMk0)*ldk;
Eneval0 = sum(Eulk+Edlk);
end
end
energy = [energy, Eneval];
end
plot(energy,'-*');
grid on;
But when I change the variables “Wul, Wdl, FC, BIk, BOk, Tmax” as
Wul = 1e7; Wdl = 1e7;
FC = 10^10;
BIk = 1e4ones(1,k);
BOk = 1e4ones(1,k);
Tmax = 0.15;
I got the result successfully as followed,
Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 533 variables, 222 equality constraints
24 exponentials add 192 variables, 120 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
12/ 12 | 2.977e+00 1.832e+00 0.000e+00 | Inaccurate/Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Inaccurate/Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Inaccurate/Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Inaccurate/Solved
Status: Inaccurate/Solved
Optimal value (cvx_optval): +2.84554
I have controlled the value of variables in the constraints, what cause the error happened?
Thank you!