Hello, everyone!
I express the constraint as follows, I want to know whether it is right?
square( pow_pos( V2(n),-a/2) + pow_pos(V3(n),-1) ) <=constant
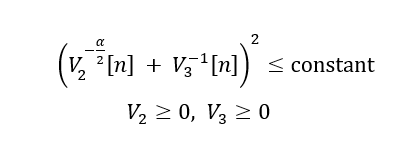
Hello, everyone!
I express the constraint as follows, I want to know whether it is right?
square( pow_pos( V2(n),-a/2) + pow_pos(V3(n),-1) ) <=constant
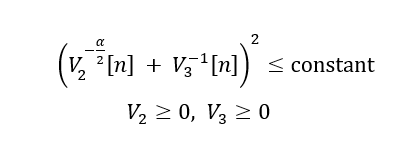
Use pow_p, not pow_pos. For the 2nd term, you also could use inv_pos
help pow_pos
pow_pos Power of positive part.
pow_pos(X,P) = POS(X).^P = MAX(X,0).^P.
Both P and X must be real, and P must be greater than or equal to 1.Disciplined convex programming information: pow_pos(X,P) is convex and nondecreasing in X; so when used in CVX expressions, X must be convex. P must be constant, real, and greater than or equal to 1.
help pow_p
pow_p Positive branch of the power function.
pow_p(X,P) computes a convex or concave branch of the power function:
P < 0: pow_p(X,P) = X.^P if X > 0, +Inf otherwise
0 <= P < 1: pow_p(X,P) = X.^P if X >= 0, -Inf otherwise
1 <= P : pow_p(X,P) = X.^P if X >= 0, +Inf otherwise
Both P and X must be real.Disciplined convex programming information: The geometry of pow_p(X,P) depends on the precise value of P, which must be a real constant: P < 0: convex and nonincreasing; X must be concave. 0 <= P < 1: concave and nondecreasing; X must be concave. 1 <= P : convex and nonmonotonic; X must be affine. In all cases, X must be real.
Thank you for your reply, I have modified my code.
But have another problem about ‘‘Cannot perform the operation: {complex affine} . {convex}*’’. The constraint and my code are as follows:
Sx(n) = Xe(n) * pow_p( V2(n) , - alpha ) ;
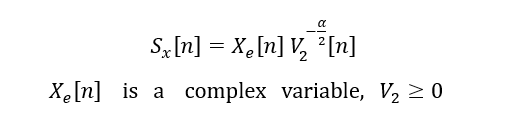
Sorry, Xe[n] is a complex constant
That is non-convex. it would be non-convex (neither convex nor concave) even if X were real rather than complex. It would be non-convex, even if V were not raised to any power.
I don’t know how S is used in your model, so I can’t conclude that the model is non-convex. Perhaps there is a way of reformulating the code so as to never form S, but quite possibly, such a reformulation is not possible.
Your first task is proving the optimization problem is convex.
Thank you! how to use S in my model is as follows :
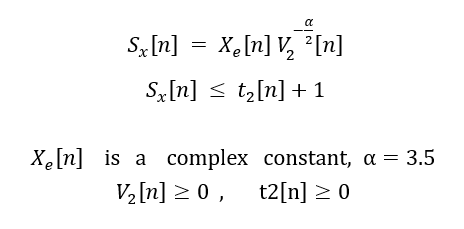
I replace Xe[n] as 2 , it not report the error.
If Xe(n) is a positive constant, that is a convex inequality. If it is not, that does not look like a convex inequality. Please carefully read the link in my previous post.
Yes, I have read your reply carefully .
It worked when I replaced the complex constant as one positive constant. So I want to know how to express the constraint for the complex constant.
Did you pay attention the the part about the constraint needing to be convex, and proving that it is?
Thank you for your time and reply!
I have already solved my problem.