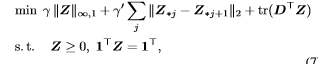I think the mixed infinity, one norm in the first term of the objective function should be
sum(norms(z,inf,1)) . No for loop is required for this norm.
Your code for this term would be correct (but not as nice as mine) if the for loop were from 1 to 100 (you got tripped up due to your second term), or if you added the i = 100 term outside the for loop.
I believe the second term is correct, but can be handled more elegantly as sum(norms(diff(z')'))
Edit: See my next post. diff can not be applied to CVX variables or expressions, so the code in the previous sentence will work only for numerical z, not for z being a CVX variable or expression.
You have not included gamma and gamma_prime in your code. Including those, you can use
minimize(gamma*sum(norms(z,inf,1)) + gamma_prime*sum(norms(diff(z')')) + trace(D'*z))
I will let you check to make sure I didn’t make a mistake. Applying the code to numerical matrices is a good way to check that the calculations are what you want.
The last constraint can be written more simply as sum(z) == 1, although your version is correct.
So it looks to me that your code is correct, but for the missing i = 100 term in the first objective term, and neglecting gamma and gamma_prime. I guess the first term in the objective, and perhaps to some extent the second term, are supposed to attempt to induce sparseness in z. However, the weights assigned to these terms via gamma and gamma_prime can have a large impact on the extent to which sparseness is induced. Optimal selection of their values is outside the scope of this form, but it is not atypical for some kind of cross-validation to be used to choose optimal values.
There is no magical “sparse matrix” designation you can use in CVX to accomplish this. Sparseness will have to be induced by your problem formulation. The mixed norm(s) in the formulation in the image are presumably trying to induce sparseness. If you really want to control sparseness, you can do it using the zero “norm” (counting number of non-zeros), but that would be non-convex, and would require use of the MIDCP capability of CVX (making use of variables declared as binary), and would be much more computationally intensive than the formulation in the image, which may not achieve the real goal quite as well, but is convex, and easy and fast to compute compared to the non-convex zero “norm” formulation.