SOS! I used SCA to optimize the variables Psi_hat, but it seemed that the value of the optimization barely changed each time and there is no upward trend

[zhen1]

My optimization problem is as follows

My code is as follows

cvx_begin
variable Psi_hat(M+1, M+1)
variable gamma_k(K,1)
variable zeta_k(K,1)
cvx_solver mosek
R_sum =0;
for k = 1:K
temp0(k) = log(exp(gamma_k(k) - zeta_k(k)))/log(2);
R_sum = R_sum + temp0(k);
end
for k = 1:K
A(:,:,k) = [F(:,:,k)W_k_ini(:,:,k)F(:,:,k)’ F(:,:,k)W_k_ini(:,:,k) H_d_H(k,:)';…
H_d_H(k, W_k_ini(:,:,k) F(:,:,k)’ 0 ];
B(:,:,k) = [F(:,:,k)diag(diag( W_k_ini(:,:,k)))F(:,:,k)’ F(:,:,k)diag(diag( W_k_ini(:,:,k))) H_d_H(k,:)';…
H_d_H(k, diag(diag( W_k_ini(:,:,k))) F(:,:,k)’ 0 ];
Z(:,:,k) =diag([H_r_H(k, 0])* diag([H_r_H(k,:)‘;0]);
end
for k = 1:K
C(:,:,k) =[(G*W_k_ini(:,:,k)*G’).eye(M,M) zeros(M,1);…
zeros(1,M) 0 ];
D(:,:,k) = [(Gdiag(diag( W_k_ini(:,:,k)))*G’).*eye(M,M) zeros(M,1);…
zeros(1,M) 0 ];
end
temp1_all = 0;
for k = 1:K
temp1 (k) =real(trace(A(:,:,k)*Psi_hat)) + real(H_d_H(k,:)*W_k_ini(:,:,k)*H_d_H(k,:)');
temp1_all = temp1_all + temp1(k);
end
for k = 1:K
temp1__all (k) = temp1_all - temp1(k);
end
temp2_all = 0;
for k = 1:K
temp2 (k) =real(trace(B(:,:,k)Psi_hat)) + real(H_d_H(k,diag(diag( W_k_ini(:,:,k)))H_d_H(k,:)');
temp2_all = temp2_all + temp2(k);
end
for k = 1:K
temp3 (k) = active_noise_maxpower_originalreal(trace(Z(:,:,k)Psi_hat)) + noise_maxpower_original;
end
for k = 1:K
constraint_1(k) = abs(alpha)^2temp1_all+ alpha(1-alpha)temp2_all + temp3 (k) ;
end
for k = 1:K
constraint_5(k) = abs(alpha)^2temp1__all(k) + alpha(1-alpha)*temp2_all + temp3 (k) ;
end
temp3_1_all = 0;
for k = 1:K
temp3_1(k) = real(trace( C(:,:,k)Psi_hat));
temp3_1_all = temp3_1_all + temp3_1(k) ;
end
temp3_2_all = 0;
for k = 1:K
temp3_2(k) = real(trace( D(:,:,k)Psi_hat));
temp3_2_all = temp3_2_all+ temp3_2(k) ;
end
constraint_3= abs(alpha)^2temp3_1_all+ alpha(1-alpha)temp3_2_all + active_noise_maxpower_original(trace(Psi_hat)-1) ;

minimize -real(R_sum)
subject to
for k = 1:K
real(constraint_1(k))>= real(exp(real(gamma_k(k))))*1e8;
real(constraint_5(k))<= real(exp(relax_scaler_zeta_ini(k))*real(zeta_k(k)-relax_scaler_zeta_ini(k) + 1))*1e8;
end
real(constraint_3)<=Pr_max;
for m = 1:M
1<= diag(Psi_hat(m,m)) <=a_max;
end
diag(Psi_hat(M+1,M+1) )==1;
Psi_hat == hermitian_semidefinite(M+1);
cvx_end

My results（This value is the approximate value of the original objective function） are as follows
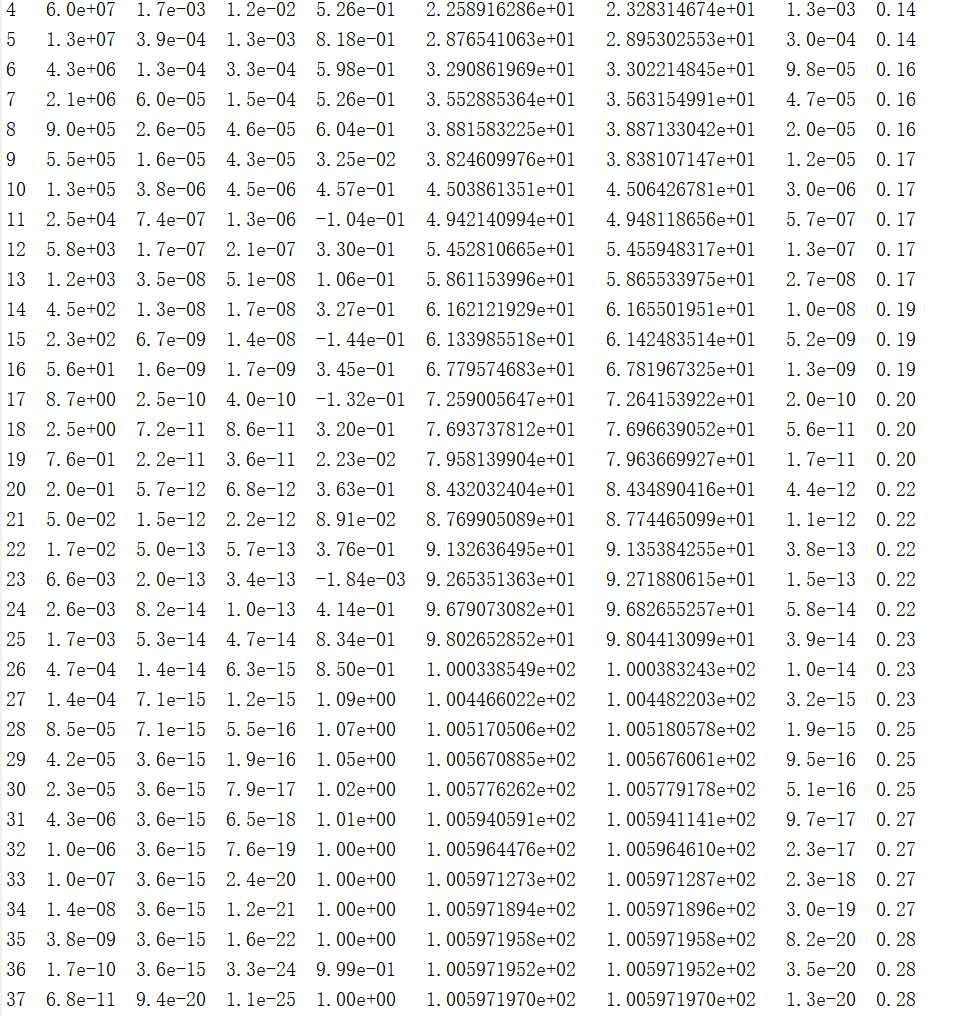
① The value of mosek solver optimization

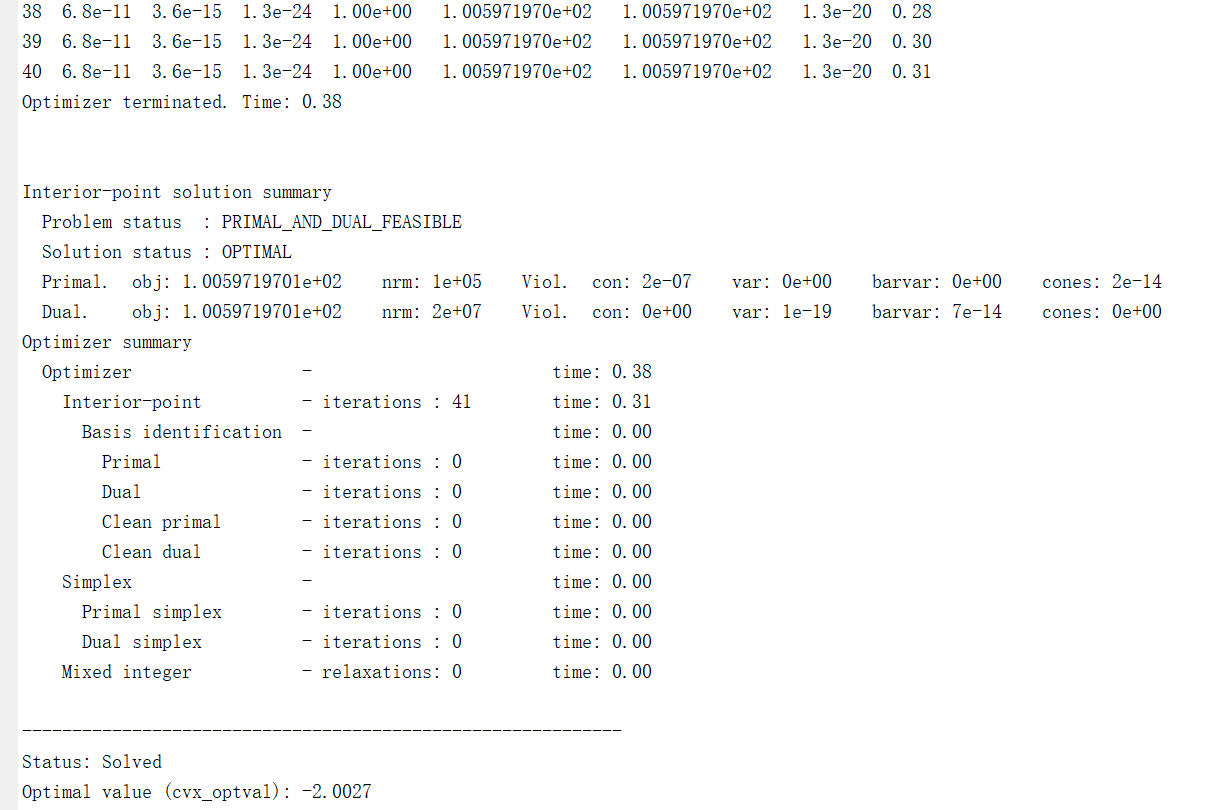
② The results displayed during the first mosek solver run

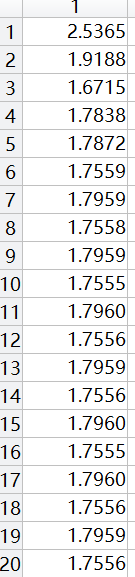
However, when I calculated the value of the original objective function with the optimized variables, the result was as follows

[Mark_L_Stone]

The result obtained using the SeDuMi solver is inaccurate. The optimal solution is not as good as before the optimization.

Unsafeguarded (no line search or trust region)Successive Convex Approximation (SCA) or generally, alternating variables optimization are unreliable. It might not descend (for minimization problem), i.e., iterates could get worse. It might not converge to anything; and if it does converge, it might not be to a local optimum of the original problem, let alone a global optimum. The solution of successive iterations, and therefore subproblem inputs, can become wilder and wilder, until at some point …

[zhen1]

Yes, I also found this post and looked at it before asking this question, and I also scaled the input values for cvx to make sure they were within 10^-5~10^5. In fact, I also used a similar SCA optimization for another variable, and the optimization results showed an upward trend in iteration, but I don’t know what the problem is here.

[Mark_L_Stone]

Sometimes SCA works well. Sometimes it doesn’t.

[zhen1]

So, in addition to setting the appropriate initial point, in your experience, when does SCA work better to achieve the desired optimization results

[Mark_L_Stone]

It works well when it works well. And doesn’t when it doesn’t.

[zhen1]

OK, fine. Thanks for your kind reply.