I want to solve SDP based optimization problem using feasibility method. The problem is formulated as
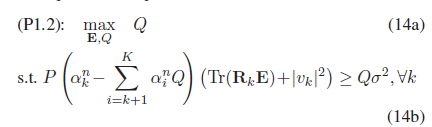
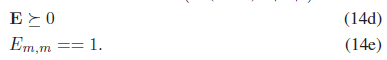
My code is as follows:
while ( qmax - qmin > tol)
q = (qmax+qmin)/2;
cvx_begin
variable QQ(N+1, N+1) hermitian semidefinite;
% feasibility problem
subject to
diag(QQ) == ones(N+1,1);
for j = 1:J
p_uni* (trace(R4(:,:,j)QQ) + (abs(Hd(:,j)))^2) >= p_uniq3((trace(R4(:,:,j)QQ) + (abs(Hd(:,j)))^2))+ qsigma2;
end
cvx_end
% bisection
if strfind(cvx_status,‘Solved’) % feasible
fprintf(1,'Problem is feasible ',q);
qmin = q;
else % not feasible
fprintf(1,‘Problem is not feasible’,q);
qmax = q;
end
end
[Uq, Dq,~] = svd(QQ);
A_Opt = 0;
for iter = 1 : 1
Rq = sqrt(0.5)(randn(N+1, 1) + 1irandn(N+1, 1));
theta = Uq * sqrt(Dq) * Rq ;
theta = theta./(theta(N+1));
theta = theta(1:N)./(abs(theta(1:N)));
A_ite = norm( G * Dh * theta , ‘fro’) ;
if A_ite > A_Opt
A_Opt = A_ite;
theta_opt = theta ;
end
end
Theta_opt = diag(theta_opt);
% total channel with random phase shifts
ht_opt = Hd+h_aiTheta_opth_ui;
abs_h1_opt = sum(abs(ht_opt).^2);
where QQ is the variable E in the picture.
At the end it shows, that the problem is solved, but there is no improvement in the final value abs_h1_opt.
Can anyone help me in this problem? I have been confused for several days and I would appreciate it if anyone can help.