SOCP problem (Inf)

[shayan66 (shayan)]

Hi,

I have difficulty in running the below op problem, which is a SOCP. It gives me a NaN or Inf as the objective value!
Could anyone give me a hint on it, please?
Thank you so much in advance.

cvx_begin
cvx_precision best
variable p(K) nonnegative
variable z(K) nonnegative
variable rho(K) nonnegative
obj=cvx(zeros(1));
for j=1:K
obj=obj+p(j);
end

minimize(obj)
subject to

p0=cvx(zeros(1));
old=cvx(zeros(1));

for i=1:K
    norm([ 2*sqrt(gamma*sigma_2) ; z(i)-rho(i) ]) <= z(i)+rho(i);

    for j=1:K
        old=p(j)*abs(w(j, : ) *H_tilda(i,:)')^2;
        p0=p0+old;
    end

    z(i)+gamma*(p0+sigma_1)==(1+gamma)*(p(i)*abs(H_tilda(i, : ) *w(i,:)')^2);
    norm([2*sqrt(e_m/eta);(1-rho(i))-p0]) <= (1-rho(i))+(p0);
    0<rho(i)<1;

end

cvx_end

[Mark_L_Stone]

I’ll give you a hint. Look at the solver and CVX Output. Perhaps they report that the problem is infeasible.

Are these the last two lines of output?

Status: Infeasible
Optimal value (cvx_optval): +Inf

If so, follow the advice in https://yalmip.github.io/debugginginfeasible/ .

I also suggest not using cvx_precision best, although I doubt that is what is causing your difficulty here.

[shayan66 (shayan)]

Thanks for your prompt reply, Mr. Stone,

The output is given by:

Status: Infeasible
Optimal value (cvx_optval): +Inf

I remove `cvx_precision best’, but it is still infeasible!
Are you suggesting me to use ‘yalmip’ instead of CVX?

[Mark_L_Stone]

No, I am suggesting you follow the advice in the link. Even though the YALMIP syntax is different than CVX syntax, the adivce still applies.

[shayan66 (shayan)]

Thanks for your help. I will check that.

[shayan66 (shayan)]

I was wondering if Mosek solver can solve it. I installed it on my Matlab. However, the main question is, how can this CVX problem be transformed into Mosek?

[Joachim_Dahl]

Changing solver won’t change whether or not the problem is feasible. A certificate of infeasibility is not an error message, it is a solution.

[Mark_L_Stone]

In order to use Mosel as the solver under CVX:

1. Re-run cvx_setup if Mosek was not installed under MASLAB when you previously installed CVX.

2. Follow the instructions at http://cvxr.com/cvx/doc/solver.html#selecting-a-solver .

As @Joachim_Dahl wrote, changing solver won’t change whether or not the problem is feasible. However, on a numerically challenging problem, it is possible Mosek will make a more reliable determination of feasibility.

In any event, please start by following the advice in https://yalmip.github.io/debugginginfeasible/ . After doing that, please feel free to ask any follow-up questions, by making additional posts in this thread,

[shayan66 (shayan)]

Thanks, that’s very kind of you. I really appreciate that.

[Erling (Erling D.Andersen)]

If you post the complete Mosek log output we can tell if reliable the conclusion about infeasibility is.

[shayan66 (shayan)]

In the above, ‘K’ is chosen to be four (K=4), which keeps giving me NaN as solutions. However, I change it to one (K=1), and it provides a solution that is neither NaN nor a desired one.

[shayan66 (shayan)]

For K=4, the output is given by

Calling Mosek 9.1.9: 56 variables, 20 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 20
Cones : 8
Scalar variables : 56
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 12
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.02
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 20
Cones : 8
Scalar variables : 56
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 8
Optimizer - Cones : 8
Optimizer - Scalar variables : 38 conic : 24
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 30 after factor : 30
Factor - dense dim. : 0 flops : 1.15e+03
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.6e+02 1.0e+00 5.0e+00 0.00e+00 3.999999996e+00 0.000000000e+00 1.0e+00 0.03
1 4.8e+01 1.9e-01 2.2e+00 -1.01e+00 4.010763615e+01 4.051628977e+01 1.9e-01 0.09
2 8.7e+00 3.4e-02 1.0e+00 -1.06e+00 2.773274536e+02 3.072967692e+02 3.4e-02 0.09
3 5.1e+00 2.0e-02 6.1e-01 -7.42e-01 3.230704606e+02 3.573896506e+02 2.0e-02 0.11
4 1.6e+00 6.2e-03 1.9e-01 -4.97e-01 3.748836904e+02 4.109663978e+02 6.2e-03 0.11
5 3.7e-01 1.4e-03 8.9e-03 1.01e+00 3.305725912e+01 3.412977867e+01 1.4e-03 0.11
6 5.1e-03 2.0e-05 1.3e-05 9.36e-01 6.270943427e-01 6.361753431e-01 2.0e-05 0.11
7 7.6e-04 3.0e-06 7.6e-07 9.86e-01 6.387855167e-02 6.551128521e-02 3.0e-06 0.13
8 2.4e-04 9.4e-07 1.8e-07 8.72e-01 9.932718665e-03 1.107346280e-02 9.4e-07 0.13
9 1.4e-04 5.4e-07 2.9e-07 6.23e-02 7.774595115e-02 8.835387752e-02 5.4e-07 0.13
10 7.0e-06 2.7e-08 3.8e-08 -4.52e-01 -7.064692065e-02 5.579064522e-03 2.7e-08 0.13
11 5.5e-09 2.1e-11 1.3e-09 -9.86e-01 -1.516532203e+02 8.776387730e-03 2.1e-11 0.13
12 5.4e-13 1.4e-20 1.4e-10 -1.00e+00 -5.480760873e+11 1.428311701e-02 9.0e-21 0.13
13 4.4e-16 2.4e-28 5.2e-10 -1.00e+00 -2.313120538e-05 -3.909637787e-31 5.0e-32 0.14
Optimizer terminated. Time: 0.17

Interior-point solution summary
Problem status : DUAL_INFEASIBLE
Solution status : DUAL_INFEASIBLE_CER
Primal. obj: -2.3131205377e-05 nrm: 6e+00 Viol. con: 4e-16 var: 0e+00 cones: 0e+00
Optimizer summary
Optimizer - time: 0.17
Interior-point - iterations : 13 time: 0.14
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

---

Status: Infeasible
Optimal value (cvx_optval): +Inf

opt_finded =

NaN

For K=1, the output is given by

Calling Mosek 9.1.9: 13 variables, 4 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 4
Cones : 2
Scalar variables : 13
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 2
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 4
Cones : 2
Scalar variables : 13
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 2
Optimizer - Cones : 2
Optimizer - Scalar variables : 9 conic : 6
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 3 after factor : 3
Factor - dense dim. : 0 flops : 5.10e+01
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.0e+00 1.0e+00 2.0e+00 0.00e+00 9.999999990e-01 0.000000000e+00 1.0e+00 0.05
1 9.2e-02 9.2e-02 3.7e-02 1.29e+00 1.524052638e-01 3.758860554e-02 9.2e-02 0.09
2 1.9e-04 1.9e-04 4.1e-06 1.09e+00 2.287314425e-04 3.432157832e-05 1.9e-04 0.09
3 7.5e-05 7.5e-05 1.2e-06 8.25e-01 7.451459667e-05 -1.429962224e-06 7.5e-05 0.11
4 3.0e-05 3.0e-05 1.0e-06 -1.97e-01 -2.158401140e-04 -1.751386096e-04 3.0e-05 0.11
5 1.8e-06 1.8e-06 1.5e-07 -3.75e-01 -3.207826087e-03 -1.647555603e-03 1.8e-06 0.11
6 1.7e-07 1.7e-07 4.2e-08 -9.48e-01 -3.344535968e-02 -1.776852399e-02 1.7e-07 0.11
7 5.1e-08 5.1e-08 1.3e-08 -5.13e-01 -8.568503478e-02 -7.024941850e-02 5.1e-08 0.11
8 6.8e-09 6.8e-09 4.7e-10 8.72e-01 -1.260155241e-01 -1.248477306e-01 6.8e-09 0.11
9 1.1e-09 1.1e-09 3.1e-11 9.25e-01 -1.334497976e-01 -1.332472006e-01 1.1e-09 0.11
10 1.2e-10 1.2e-10 1.4e-12 9.89e-01 -1.350142331e-01 -1.349832281e-01 1.2e-10 0.13
11 9.1e-13 8.7e-13 8.2e-16 9.99e-01 -1.351604447e-01 -1.351602260e-01 8.7e-13 0.13
12 1.6e-13 1.2e-14 1.9e-19 1.00e+00 -1.351615145e-01 -1.351615116e-01 1.2e-14 0.13
Optimizer terminated. Time: 0.16

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -1.3516151454e-01 nrm: 3e+03 Viol. con: 9e-11 var: 0e+00 cones: 0e+00
Dual. obj: -1.3516151156e-01 nrm: 1e+00 Viol. con: 0e+00 var: 7e-12 cones: 0e+00
Optimizer summary
Optimizer - time: 0.16
Interior-point - iterations : 12 time: 0.13
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

---

Status: Solved
Optimal value (cvx_optval): +0.135162

opt_finded =

-17.3829

[shayan66 (shayan)]

z(i)+gamma*(p0+sigma_1)==(1+gamma)*(p(i)*abs(H_tilda(i, : ) *w(i,:)’)^2);

I removed this line ‘z(i)+gamma*(p0+sigma_1)==(1+gamma)*(p(i)*abs(H_tilda(i, : ) *w(i,:)’)^2);’ from the op problem, it works for K=4!
Nevertheless, it is still confusing why K=1 has a solution, but K=4 doesn’t with the existence of that line!

[Erling (Erling D.Andersen)]

I would have high confidence to the conclusions Mosek reach at the two logs.
I can see that from the solution summaries.

[shayan66 (shayan)]

summa

Sorry, i did not understand why K=1 has a solution, but high numbers do not provide a feasible one? Could you please be more specific?

[Erling (Erling D.Andersen)]

All I can say is that the problem Mosek gets is solved correctly. That means if there is an issue then 1) cvx is buggy or 2) your model has an issue. Most likely it is option 2) that is the case. I cannot help you with that.

[shayan66 (shayan)]

I found!

Constraint ‘z(i)+gamma*(p0+sigma_1)==(1+gamma)*(p(i)*abs(H_tilda(i,: )w(:,i))^2);’ must hold true that z(i) ≥ 0. I checked the answer for ‘z(i)+(p0+sigma_1)==…’’ and then add ‘gamma’, i.e., 'z(i)+gamma(p0+sigma_1)==…’’, it is founded that z(i) is negative which is the main issue. How can i overcome this issue?

[shayan66 (shayan)]

In the first ‘for’, i set i=1:3 instead of i=1:4. It works after several iterations with Gurobi solver! But it still gives me a NaN. I am so confused!

[Mark_L_Stone]

Please show us the solver and CVX output for which “It works after several iterations with Gurobi solver!” What exactly is given to you as NaN? Please show us the NaN you are given. The output you show says Status: Inaccurate/Solved, and a non-NaN value of cvx_optval. If Status is Inaccurate/Solved, then all CVX variables, as well as cvx_optval, should not be NaN after CVX concludes.

[shayan66 (shayan)]

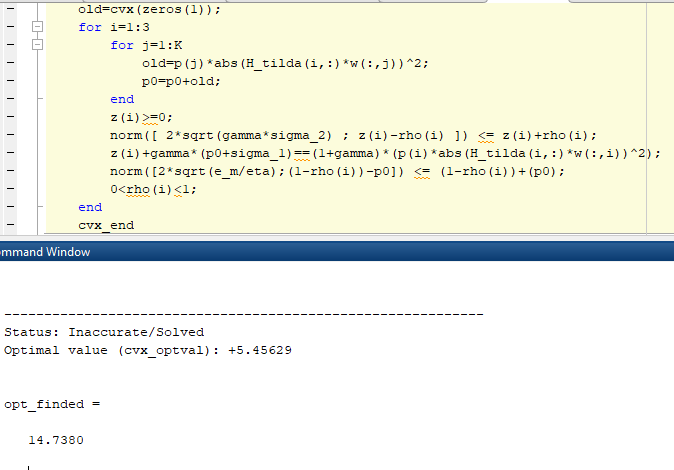
I used Mosek solver. The result for K=2 is as follows:
Note that i run the CVX for 5 times, and average over all realizations(=5).

Calling Mosek 9.1.9: 32 variables, 10 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 6
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.02
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 4
Optimizer - Cones : 4
Optimizer - Scalar variables : 20 conic : 12
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 9 after factor : 10
Factor - dense dim. : 0 flops : 2.46e+02
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 8.2e+03 1.0e+00 3.0e+00 0.00e+00 1.999999999e+00 0.000000000e+00 1.0e+00 0.05
1 6.3e+02 7.8e-02 8.3e-01 -9.99e-01 4.942182388e+01 5.928395281e+01 7.8e-02 0.13
2 1.2e+01 1.4e-03 1.0e-01 -9.93e-01 2.310350387e+03 2.884738353e+03 1.4e-03 0.13
3 4.6e+00 5.6e-04 4.4e-02 -5.58e-01 3.012553752e+03 3.696342093e+03 5.6e-04 0.14
4 1.7e+00 2.0e-04 3.2e-03 8.29e-01 3.815868327e+02 4.093445805e+02 2.0e-04 0.14
5 4.4e-02 5.4e-06 1.4e-05 8.03e-01 2.362313261e+01 2.432621877e+01 5.4e-06 0.14
6 2.2e-03 2.7e-07 1.6e-07 1.00e+00 8.651567221e-01 9.007351459e-01 2.7e-07 0.14
7 8.8e-04 1.1e-07 5.4e-08 9.61e-01 2.616489753e-01 2.893341733e-01 1.1e-07 0.16
8 5.4e-04 6.6e-08 3.8e-08 6.15e-01 -3.141143559e-03 3.272972751e-02 6.6e-08 0.17
9 1.7e-04 2.0e-08 9.4e-09 5.92e-01 -3.468586474e-01 -3.231969212e-01 2.0e-08 0.17
10 5.9e-05 7.2e-09 3.1e-09 9.66e-02 -7.333085016e-01 -7.123205550e-01 7.2e-09 0.17
11 1.0e-05 1.3e-09 2.5e-10 9.00e-01 -9.956292703e-01 -9.915235489e-01 1.3e-09 0.17
12 1.5e-06 1.8e-10 1.5e-11 9.80e-01 -1.053817253e+00 -1.053075772e+00 1.8e-10 0.17
13 5.3e-07 6.4e-11 3.4e-12 1.01e+00 -1.061157348e+00 -1.060850572e+00 6.4e-11 0.19
14 9.4e-08 1.1e-11 2.5e-13 1.02e+00 -1.063919087e+00 -1.063866544e+00 1.1e-11 0.19
15 1.9e-08 2.2e-12 2.2e-14 1.03e+00 -1.064390713e+00 -1.064379727e+00 2.2e-12 0.19
16 1.2e-08 1.1e-13 1.7e-16 1.01e+00 -1.064510737e+00 -1.064510313e+00 8.5e-14 0.19
17 2.1e-09 1.1e-13 8.1e-19 1.00e+00 -1.064515574e+00 -1.064515570e+00 8.0e-16 0.20
Optimizer terminated. Time: 0.27

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -1.0645155743e+00 nrm: 3e+04 Viol. con: 2e-09 var: 0e+00 cones: 0e+00
Dual. obj: -1.0645155703e+00 nrm: 1e+00 Viol. con: 0e+00 var: 3e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 0.27
Interior-point - iterations : 17 time: 0.20
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

---

Status: Solved
Optimal value (cvx_optval): +1.06452

Calling Mosek 9.1.9: 32 variables, 10 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 6
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 4
Optimizer - Cones : 4
Optimizer - Scalar variables : 19 conic : 12
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 9 after factor : 10
Factor - dense dim. : 0 flops : 2.40e+02
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 4.1e+03 1.0e+00 3.0e+00 0.00e+00 1.999999999e+00 0.000000000e+00 1.0e+00 0.03
1 3.3e+01 8.1e-03 2.7e-01 -1.00e+00 4.903035667e+02 6.103948392e+02 8.1e-03 0.11
2 8.2e+00 2.0e-03 1.3e-01 -9.62e-01 1.760297032e+03 2.193933657e+03 2.0e-03 0.11
3 3.7e+00 8.9e-04 3.9e-02 -3.23e-01 1.116764873e+03 1.326921494e+03 8.9e-04 0.11
4 3.9e-01 9.5e-05 1.2e-03 4.74e-01 2.394489778e+02 2.569244382e+02 9.5e-05 0.13
5 2.3e-03 5.6e-07 4.8e-07 1.04e+00 7.463056147e-01 8.264297379e-01 5.6e-07 0.13
6 5.5e-04 1.3e-07 6.1e-08 9.87e-01 6.235316085e-02 8.551034976e-02 1.3e-07 0.13
7 2.4e-04 5.8e-08 2.8e-08 7.54e-01 -7.574319903e-02 -4.938319655e-02 5.8e-08 0.13
8 9.0e-05 2.2e-08 1.4e-08 2.98e-01 -1.891179260e-01 -1.436236838e-01 2.2e-08 0.13
9 1.3e-05 3.2e-09 1.0e-08 -1.12e+00 -7.118921736e-01 3.699800526e-01 3.2e-09 0.13
10 2.1e-08 4.8e-12 2.5e-10 -9.11e-01 -2.989154374e+02 2.577776937e-02 4.8e-12 0.14
11 4.6e-10 5.1e-20 1.3e-10 -1.00e+00 -3.338692711e+10 1.672495727e-02 4.8e-20 0.14
12 4.4e-16 8.8e-26 1.5e-10 -1.00e+00 -2.969966148e-05 2.767397087e-26 8.1e-30 0.14
Optimizer terminated. Time: 0.17

Interior-point solution summary
Problem status : DUAL_INFEASIBLE
Solution status : DUAL_INFEASIBLE_CER
Primal. obj: -2.9699661481e-05 nrm: 5e+00 Viol. con: 4e-16 var: 0e+00 cones: 0e+00
Optimizer summary
Optimizer - time: 0.17
Interior-point - iterations : 12 time: 0.14
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

---

Status: Infeasible
Optimal value (cvx_optval): +Inf

Calling Mosek 9.1.9: 32 variables, 10 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 6
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.01
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 4
Optimizer - Cones : 4
Optimizer - Scalar variables : 20 conic : 12
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 9 after factor : 10
Factor - dense dim. : 0 flops : 2.46e+02
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 2.0e+03 1.0e+00 3.0e+00 0.00e+00 1.999999999e+00 0.000000000e+00 1.0e+00 0.03
1 3.4e+01 1.7e-02 3.8e-01 -9.98e-01 2.251777964e+02 2.790814263e+02 1.7e-02 0.11
2 6.8e+00 3.3e-03 1.4e-01 -8.79e-01 8.320392205e+02 1.032763735e+03 3.3e-03 0.11
3 2.2e+00 1.1e-03 1.0e-02 -3.03e-02 1.847148333e+02 1.936482058e+02 1.1e-03 0.13
4 1.0e-01 5.1e-05 9.4e-05 8.00e-01 1.504078917e+01 1.538758372e+01 5.1e-05 0.13
5 2.0e-03 9.8e-07 2.5e-07 1.01e+00 1.713581927e-01 1.778206823e-01 9.8e-07 0.13
6 7.7e-04 3.8e-07 8.7e-08 9.87e-01 2.566820890e-02 3.125321368e-02 3.8e-07 0.13
7 4.3e-04 2.1e-07 5.5e-08 6.23e-01 -2.358459714e-02 -1.603890853e-02 2.1e-07 0.13
8 9.2e-05 4.5e-08 1.1e-08 3.73e-01 -1.139105409e-01 -1.067212387e-01 4.5e-08 0.13
9 2.1e-05 1.0e-08 1.6e-09 2.59e-01 -2.422997654e-01 -2.395794652e-01 1.0e-08 0.14
10 3.8e-06 1.9e-09 1.3e-10 9.03e-01 -2.797273792e-01 -2.791873727e-01 1.9e-09 0.14
11 1.1e-06 5.5e-10 2.2e-11 9.90e-01 -2.861373766e-01 -2.859676605e-01 5.5e-10 0.14
12 2.0e-07 1.0e-10 1.9e-12 1.01e+00 -2.885866513e-01 -2.885455033e-01 1.0e-10 0.14
13 4.0e-08 2.2e-11 1.9e-13 1.04e+00 -2.889303957e-01 -2.889216995e-01 2.2e-11 0.14
14 7.5e-09 2.6e-12 7.6e-15 1.03e+00 -2.890214532e-01 -2.890204579e-01 2.5e-12 0.16
15 3.8e-09 8.4e-14 5.1e-18 1.00e+00 -2.890332790e-01 -2.890332758e-01 8.6e-15 0.16
Optimizer terminated. Time: 0.19

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -2.8903327904e-01 nrm: 7e+03 Viol. con: 2e-09 var: 0e+00 cones: 0e+00
Dual. obj: -2.8903327577e-01 nrm: 1e+00 Viol. con: 0e+00 var: 6e-12 cones: 0e+00
Optimizer summary
Optimizer - time: 0.19
Interior-point - iterations : 15 time: 0.16
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

---

Status: Solved
Optimal value (cvx_optval): +0.289033

Calling Mosek 9.1.9: 32 variables, 10 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 6
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.03
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 4
Optimizer - Cones : 4
Optimizer - Scalar variables : 20 conic : 12
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 9 after factor : 10
Factor - dense dim. : 0 flops : 2.46e+02
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.6e+04 1.0e+00 3.0e+00 0.00e+00 1.999999999e+00 0.000000000e+00 1.0e+00 0.03
1 3.5e+01 2.2e-03 1.4e-01 -1.00e+00 1.744664877e+03 2.178446970e+03 2.2e-03 0.11
2 1.0e+01 6.3e-04 6.3e-02 -8.64e-01 4.590998145e+03 5.705970792e+03 6.3e-04 0.11
3 4.7e+00 2.9e-04 9.1e-03 5.83e-02 1.152452861e+03 1.261706834e+03 2.9e-04 0.11
4 3.8e-01 2.3e-05 2.3e-04 5.99e-01 2.264695650e+02 2.373581419e+02 2.3e-05 0.13
5 3.7e-03 2.3e-07 2.1e-07 1.01e+00 1.351291529e+00 1.448390172e+00 2.3e-07 0.13
6 9.5e-04 5.8e-08 3.2e-08 1.00e+00 9.076172173e-02 1.245863735e-01 5.8e-08 0.13
7 5.0e-04 3.0e-08 1.8e-08 8.15e-01 -1.542997652e-01 -1.161458241e-01 3.0e-08 0.13
8 2.0e-04 1.2e-08 7.1e-09 6.02e-01 -3.905111144e-01 -3.517166426e-01 1.2e-08 0.13
9 7.9e-05 4.8e-09 3.3e-09 -2.44e-01 -9.773429117e-01 -9.235279259e-01 4.8e-09 0.14
10 7.0e-06 4.3e-10 8.5e-11 8.45e-01 -1.602306755e+00 -1.597896469e+00 4.3e-10 0.14
11 1.5e-06 9.1e-11 8.9e-12 9.77e-01 -1.659023834e+00 -1.657967195e+00 9.1e-11 0.14
12 4.7e-07 2.9e-11 1.7e-12 1.01e+00 -1.672049689e+00 -1.671646985e+00 2.9e-11 0.14
13 8.5e-08 5.4e-12 1.4e-13 1.03e+00 -1.675882757e+00 -1.675809755e+00 5.4e-12 0.14
14 3.1e-08 1.1e-12 1.2e-14 1.04e+00 -1.676616507e+00 -1.676602298e+00 1.1e-12 0.14
15 5.0e-09 1.3e-14 4.2e-18 1.01e+00 -1.676799268e+00 -1.676799197e+00 5.0e-15 0.16
16 4.9e-09 6.6e-14 7.5e-18 1.00e+00 -1.676800156e+00 -1.676800157e+00 3.6e-17 0.16
Optimizer terminated. Time: 0.19

Interior-point solution summary
Problem status : PRIMAL_AND_DUAL_FEASIBLE
Solution status : OPTIMAL
Primal. obj: -1.6768001564e+00 nrm: 4e+04 Viol. con: 1e-08 var: 0e+00 cones: 0e+00
Dual. obj: -1.6768001572e+00 nrm: 2e+00 Viol. con: 0e+00 var: 3e-10 cones: 0e+00
Optimizer summary
Optimizer - time: 0.19
Interior-point - iterations : 16 time: 0.16
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

---

Status: Solved
Optimal value (cvx_optval): +1.6768

Calling Mosek 9.1.9: 32 variables, 10 equality constraints
For improved efficiency, Mosek is solving the dual problem.

MOSEK Version 9.1.9 (Build date: 2019-11-21 11:34:40)
Copyright © MOSEK ApS, Denmark. WWW: mosek.com
Platform: Windows/64-X86

Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer started.
Presolve started.
Linear dependency checker started.
Linear dependency checker terminated.
Eliminator started.
Freed constraints in eliminator : 6
Eliminator terminated.
Eliminator started.
Freed constraints in eliminator : 0
Eliminator terminated.
Eliminator - tries : 2 time : 0.00
Lin. dep. - tries : 1 time : 0.00
Lin. dep. - number : 0
Presolve terminated. Time: 0.01
Problem
Name :
Objective sense : min
Type : CONIC (conic optimization problem)
Constraints : 10
Cones : 4
Scalar variables : 32
Matrix variables : 0
Integer variables : 0

Optimizer - threads : 2
Optimizer - solved problem : the primal
Optimizer - Constraints : 4
Optimizer - Cones : 4
Optimizer - Scalar variables : 20 conic : 12
Optimizer - Semi-definite variables: 0 scalarized : 0
Factor - setup time : 0.00 dense det. time : 0.00
Factor - ML order time : 0.00 GP order time : 0.00
Factor - nonzeros before factor : 9 after factor : 10
Factor - dense dim. : 0 flops : 2.46e+02
ITE PFEAS DFEAS GFEAS PRSTATUS POBJ DOBJ MU TIME
0 1.6e+04 1.0e+00 3.0e+00 0.00e+00 1.999999999e+00 0.000000000e+00 1.0e+00 0.03
1 1.2e+01 7.5e-04 8.0e-02 -1.00e+00 4.963394117e+03 6.201872367e+03 7.5e-04 0.11
2 5.5e+00 3.3e-04 4.2e-02 -7.60e-01 7.503087814e+03 9.277537617e+03 3.3e-04 0.11
3 2.7e+00 1.7e-04 4.0e-03 9.23e-01 9.968654413e+02 1.059694099e+03 1.7e-04 0.11
4 1.6e-01 9.5e-06 5.9e-05 6.71e-01 1.461240985e+02 1.503426382e+02 9.5e-06 0.11
5 4.2e-03 2.6e-07 2.6e-07 1.01e+00 2.886806537e+00 2.999734966e+00 2.6e-07 0.13
6 8.3e-04 5.1e-08 3.2e-08 9.80e-01 3.542952004e-01 3.976504073e-01 5.1e-08 0.13
7 2.4e-04 1.5e-08 1.0e-08 7.49e-01 -2.792978649e-01 -2.294361343e-01 1.5e-08 0.13
8 1.3e-04 7.8e-09 8.1e-09 -1.76e-02 -5.614453852e-01 -4.413734050e-01 7.8e-09 0.13
9 4.1e-05 2.5e-09 2.9e-09 -8.87e-02 -1.531958641e+00 -1.378406643e+00 2.5e-09 0.13
10 8.8e-06 5.4e-10 2.5e-09 -1.13e+00 -3.530626158e+00 -1.124349954e+00 5.4e-10 0.14
11 1.1e-07 6.9e-12 3.3e-10 -1.01e+00 -2.606864433e+02 -1.366252618e+00 6.9e-12 0.14
12 2.2e-12 1.2e-17 1.8e-11 -1.00e+00 -2.015224479e+08 -1.497137394e+00 1.2e-17 0.14
13 4.4e-16 5.5e-23 8.0e-13 -1.00e+00 -1.813665146e-05 -3.212423233e-22 9.7e-27 0.14
Optimizer terminated. Time: 0.17

Interior-point solution summary
Problem status : DUAL_INFEASIBLE
Solution status : DUAL_INFEASIBLE_CER
Primal. obj: -1.8136651460e-05 nrm: 9e+00 Viol. con: 4e-16 var: 0e+00 cones: 0e+00
Optimizer summary
Optimizer - time: 0.17
Interior-point - iterations : 13 time: 0.14
Basis identification - time: 0.00
Primal - iterations : 0 time: 0.00
Dual - iterations : 0 time: 0.00
Clean primal - iterations : 0 time: 0.00
Clean dual - iterations : 0 time: 0.00
Simplex - time: 0.00
Primal simplex - iterations : 0 time: 0.00
Dual simplex - iterations : 0 time: 0.00
Mixed integer - relaxations: 0 time: 0.00

---

Status: Infeasible
Optimal value (cvx_optval): +Inf

opt_finded =

0.0874