Hi, I am trying to use CVX to maximize the sum of transmission rate and I encountered some problems. I know shannon formula: x*log(1+y/x) is jointly concave with x and y. But CVX failed to optimize it and the optimized result worse than the initial result. I am really confused about that and want to seek some help. Here are my codes:
%%
clc;clear;
N = 30; %The number of users
h = cell2mat(struct2cell(load(‘path_loss_model.mat’,‘path_loss’)));
h = h(1:30);
B_tot = 20e6; % total bandwidth
p_tot = 40; % dbm
p_tot_w = 10^(p_tot/10)/1e3;
N0 = 10.^(-20.4); % noise spectral density
pn = ones(N,1)*p_tot_w/N;
Bn = ones(N,1)*B_tot/N;
pmin = 1e-3;
h_N0 = h./N0;
r_temp = sum(-rel_entr(Bn,Bn+(pn.*h_N0)));
fprintf(‘total transmission rate: %e\n’, r_temp)
%%
cvx_begin
variables p(N) B(N)
maximize sum(-rel_entr(B,B+(p.*h_N0)))
subject to
0 <= p
0 <= B
sum(B) <= B_tot;
sum(p) <= p_tot_w;
cvx_end
r = sum(-rel_entr(B,B+(p.*h_N0)))
fprintf(‘optimized total transmission rate: %e\n’, r)
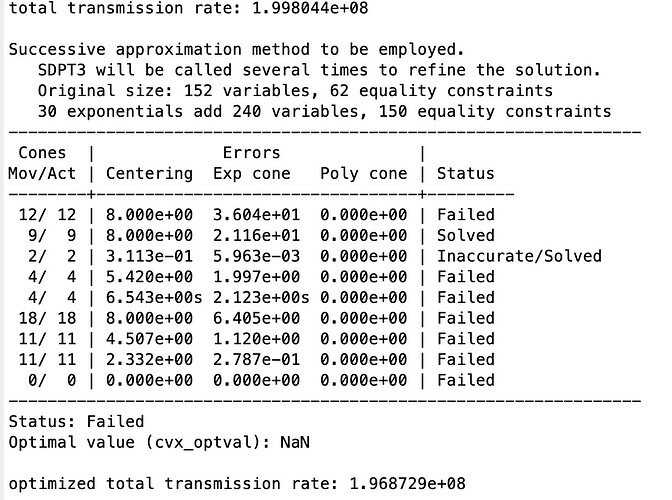
and the result shows:
Thank you very much!