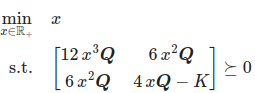Semdefinite constraint with cubic entry

Nonconvex
1

Hi all,
I am trying to solve the following optimization problem:

image

where Q \in \mathbb{S}^2_{++} is a known constant matrix and K is another known constant matrix. The optimization variable x \in \mathbb{R}_{+} is nonnegative. I started by setting K = \mathbf{0} i.e. a zero matrix. In this case, there is a trivial solution x = 0, however, the presence of the cubic and quadratic terms seems to violate the Disciplined Convex Programming rules. Since x is nonnegative, the constraint should be a convex constraint. Is there a way to formulate this problem in a manner that is consistent with DCP rules?

I am reading up on similar posts here to see if power cones would be applicable. Any suggestions would be appreciated. Thanks.

2

That is a Polynomial Matrix Inequality, which can be lifted to a Bilinear Matrix Inequality (BMI), and is non-convex, unless there is some transformation I haven’t considered. If I am overlooking something, other people should feel free to provide an appropriate reformulation.

You can try using YALMIP (which I believe will automatically reformulate this as a BMI) on this with either a local solver or the BMIBNB global solver. It is only a one variable problem, so perhaps it is rather easy to solve to global optimality.

As for convexity, power cones, etc, keep in kind this is an SDP constraints, so those other posts are not applicable.

3

Hi Mark,
Thanks for getting back to me. I was able to get some results with the combination of YALMIP + BNIB. In some cases, there were numerical warnings but in the end, it worked out. However, I would like to have some theoretical guarantees.

And so I am trying another approach based on relaxing the problem to SDP. I am able to reformulate the problem into the following form:

\begin{equation} \begin{aligned} \min_{\mathbf{X}\in \mathbb{R}^{3 \times 3}} \quad & \mathrm{tr}(\mathbf{A}\mathbf{X}) \\ \text{s.t.} \quad & \mathrm{tr}(\mathbf{B}_{0} \mathbf{X}) = 1 \\ \quad & \mathrm{tr}(\mathbf{B}_{i} \mathbf{X}) = 0, \quad i \in \{ 1,2,3 \} \\ \quad & \mathbf{X} \succeq 0 \\ \quad & \mathbf{J} \succeq 0 \end{aligned} \end{equation}
\begin{align*} \mathbf{A} = \begin{bmatrix} 0 & 0.5 & 0 & 0\\ 0.5 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, ~ \mathbf{B}_{0} \begin{bmatrix} 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix}, ~ \mathbf{B}_{1} = \begin{bmatrix} 0 & 0 & 1 & 0\\ 0 & -2 & 0 & 0 \\ 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 \end{bmatrix} \end{align*}
\begin{align*} \mathbf{B}_{2} = \begin{bmatrix} 0 & 0 & 0 & 1\\ 0 & 0 & -1 & 0 \\ 0 & -1 & 0 & 0 \\ 1 & 0 & 0 & 0 \end{bmatrix} \mathbf{B}_{3} = \begin{bmatrix} 0 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 \\ 0 & 0 & -2 & 0 \\ 0 & 1 & 0 & 0 \end{bmatrix} \end{align*}
J = \begin{bmatrix} 12 \boldsymbol{Q} \, \mathbf{X}(1,2) & 6 \boldsymbol{Q} \, \mathbf{X}(1,1) \\ 6 \boldsymbol{Q} \, \mathbf{X}(1,1) & 6 \boldsymbol{Q} \, \mathbf{X}(0,1) \\ \end{bmatrix}

I drop the rank constraint \textrm{rank}(\mathbf{X}) = 1. I am following the idea of sum-of-squares relaxation (https://www.princeton.edu/~aaa/Public/Teaching/ORF523/ORF523_Lec15.pdf) approach to obtain the SDP relaxation. The additional constraints (\mathbf{B}_i, i=(1,2,3)) are necessary for tightness (to potentitally obtain rank-1 solution).

However, I am getting a new error this time while solving using MOSEK solver:

CVXPY) May 10 04:44:41 PM: Optimizer terminated. Time: 0.01
(CVXPY) May 10 04:44:41 PM:
(CVXPY) May 10 04:44:41 PM:
(CVXPY) May 10 04:44:41 PM: Interior-point solution summary
(CVXPY) May 10 04:44:41 PM: Problem status : UNKNOWN
(CVXPY) May 10 04:44:41 PM: Solution status : UNKNOWN
(CVXPY) May 10 04:44:41 PM: Primal. obj: 5.5498901606e-01 nrm: 1e+00

I am new to CVXPY with MOSEK and don’t quite know how to go about debugging this issue.

Also, I am not sure if I should start a different thread for this since I reformulated the problem and the solution proposed by Mark works with the original formulation. If so the case, I can start a new thread.

4

This is the CVX forum, not a CVXPY forum. In any event, it appears Mosek had numerical difficulties with your problem. Perhaps the SOS is ill-conditioned/

If you use YALMIP for SOS, you may be better able to get useful help at the YALMIP forum.

5

Thanks Mark. Apologies for asking a CVXPY-related question. I’ll try YALMIP for this and update here about the results.