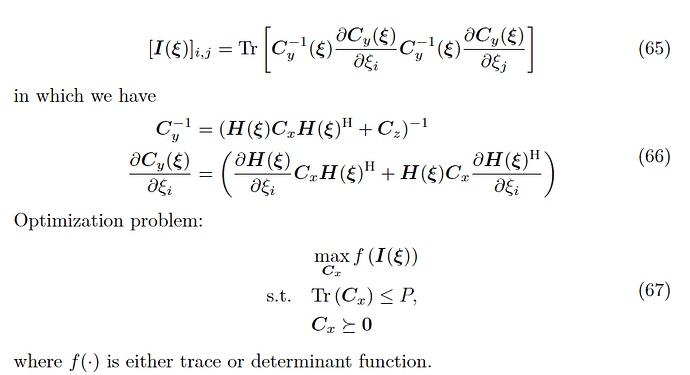Hello! I encounter recently the following optimization problem which tries to maximize the trace or determinant of Fisher information matrix:
in which
C_x,
C_z are PSD matrices,
H(\xi) is a matrix depending on
\xi, and
\xi_i is the
i-th component of
\xi.
I would like to know if there’s a way to rewrite this problem such that it fulfills DCP rules.
Thank you very much in advance!
The first step is for you to formulate the problem explicitly in terms of optimization variables (C_x?) and input data (everything else, including all the derivatives?). Are there unstated relationships between any of these things? Why is the objective written as a function of \zeta? If \zeta is fixed, what s the meaning of any of this, and if it is a variable, what is it related to? Or things are a function of \zeta, differentiated with respect to \zeta, and then the value of \zeta is fixed at some particular value to evaluate this, rendering everything other than C_x as numerical input data? I don’t understand any of that. Hopefully you do, and if not, will more carefully study whatever paper or book this comes from, if not your own.
The next step is for you to prove this is a convex optimization problem, which looks very doubtful to me.
Sorry for the unclear description.
Yes, C_x is the optimization variable. \xi doesn’t play a role here and we consider it as a constant in the optimization problem. Writing I(\xi) just want to emphasize the derivative of H with respect to it.
The overall problem is maximizing the trace or determinant of matrix I over a PSD matrix C_x. H, dH/d\xi_i are both constant matrices, C_z is a PSD constant matrix. Hopefully it makes my question clear now.
Regarding its convexity, to be honest, I tried but didn’t find a way to verify it.
It doesn’t look convex to me. I will assume it is not, unless you show otherwise.