i am working on radio resource allocation for GEO satellite. I run some optimization code with cvx and it is giving me error. The cvx sometimes solve it and sometimes it is inaccurate plus the value of cvx-optval is not right
Can you copy and paste your program, using Preformatted text icon, preferably complete with all input data? Then show the solver and CVX output, together with your evidence and explanation of supposed incorrectness?
A common thing which causes inaccurate or incorrect answers is bad numerical scaling of input data. All no-zero input data should be within a small number of orders of magnitude of one; otherwise the results might be inaccurate, “incorrect”, and/or the solver might encounter numerical difficulties.
close all
clear
%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Fixed parameters %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
satellite_location = [13 0]; %point A below star
%beamcenter_location = [114.14 22.02; 120.38 22.48; 107.32 27.4; 114.17 28.56; 120.86 28.11; 108.86 34; 116.191 33.571]; %beam center coordinates
%beamcenter_location = [114.14 22.02 120.38 22.48 107.32 27.4 114.17 28.56 120.86 28.11 108.86 34 116.191 33.571 110.5 23.7 118.9 34.1 123.3 25.2 106.6 26.8 98.7 18.4 105.8 27.7 109.4 27.8 101.0 22.0 97.8 21.3 104.7 30.7 115.2 27.1 98.0 25.7 111.1 29.7 118.7 24.9 120.0 36.1 121.2 31.3 99.8 21.3 117.7 34.4 112.1 27.3 98.1 26.3 110.3 28.6 112.1 24.5 113.9 26.5 118.9 24.5 98.8 24.2 103.7 23.0 120.9 31.4 106.5 23.8 107.6 30.4 112.1 23.5 115.6 34.3 117.5 36.2 118.9 25.8 120.3 33.0 106.6 26.0 112.7 28.3 119.6 27.6 121.2 31.2 99.6 20.9 103.9 23.5 109.6 28.8 110.4 22.4 111.6 33.6 115.5 31.3 116.4 27.4 118.4 29.1 119.3 31.3 120.7 33.0 121.9 25.0 104.0 30.7 106.8 28.2 113.7 24.9 118.0 27.3 118.2 30.7 120.2 28.9 121.7 25.1];
beamcenter_location =[16.37 48.20;11.58 48.14; 17.70 53.97; 12.49 41.89; 15.99 45.81; 13.41 52.51;12.56 55.68];
N = size(beamcenter_location, 1) % number of beams,number of row read
M = 12; %number of ground station
B1 = 11.7 * 1e9; % lower bound of available bandwidth
B2 = 12.2 * 1e9; % upper bound of available bandwidth Hz
Btot =B2-B1; % total carrier width
% SINR_min_dB = -5.23;
SINR_min_dB = -2.2;
SINR_min = 10^(SINR_min_dB/10); % 0.3
Bc = 5e6; % minimum bandwidth(Hz)
N0_dB = -204; % Bottom Noise dBW / Hz
N0 = 10^(N0_dB/10);
G_dB = 52; % Maximum beam gain (51.8dBi)
G = 10^(G_dB/10);
GR_dB = 39.8;
GR = 10^(GR_dB/10); % user antenna gain(39.8dBi)
Ptotal = 1000; % Total avaiable transmit power(W)
Pmax = 100; % Maximum power beam(W)
lamda = 3e8 / (11.951e9); % Wavelength (m)
demand_mean = 300; % Average of demand1e6 (bps)(bps)
%%%%%%%%%%%%%%%%%%%%%%%%% random ground station locations, user requirments %%%%%%%%%%%%%%%%%%%%%%%%
% import polygon vertex coordinates
%tx = xlsread(‘cell.xlsx’);
%xx = tx(:,1);
%yy = tx(:,2);
% random distribution, the specified number points
%user_location = zeros(M,2);
%n = 1;
%while (n <= M)
%xp = 100+30rand;
%yp = 18+20rand;
%if inpolygon(xp,yp,xx,yy)
%user_location(n,1) = xp;
%user_location(n,2) = yp;
%n = n+1;
%end
%end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Fixed Earth Station Position %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%user_location =[16.78 49.73;11.61 48.18;15.12 45.32;13.71 53.44;12.51 41.81;17.46 52.42;14.06 47.10;15.62 50.55;13.90 58.74;12.45 41.87]
user_location =[16.78 49.73;12.85 45.61;11.61 48.18;15.12 45.32;13.71 53.44;12.56 41.86;12.51 41.81;17.46 52.42;14.06 47.10;15.62 50.55;13.90 58.74;11.99 48.81;12.45 41.87]
% normal distribution of random user demand
demand = normrnd(demand_mean, 50, M, 1)1e6 ; % user requirements bps, the total amount of reources that seven beam can provide is 4.031e9(bps)
for m = 1:M
if demand(m) < 0
demand(m) = 1e6;
end
end
%%%%%%%%%%%%%%%%%%%%%%% convert a plurality of user within a beam into a %%%%%%%%%%%%%%%%%%%%%
distance_userandbeam = zeros(M, N);
closestbeamcenter = zeros(M, 1); % give the intial value of a by distance
demand_in_beam = zeros(N, 1); % sum of all user requirment within the beam
% is the approximate user requirment
for m = 1:M
for n = 1:N
distance_userandbeam(m,n) = distance_sky2ground(user_location(m,:), beamcenter_location(n,:));
end
% The nearest beam to the mth user is closestbeamcenter(m)
closestbeamcenter(m) = find(distance_userandbeam(m,![]() == min(distance_userandbeam(m,:)), 1);
== min(distance_userandbeam(m,:)), 1);
end
% generate approximate user
for m = 1:M
for n = 1:N
if (closestbeamcenter(m) == n)
demand_in_beam(n) = demand_in_beam(n) + demand(m);
end
end
end
% randomly select one of the users accessing the nth beam
superuser_location_in_beam = zeros(N, 2);
for n = 1:N
user_in_beam = find(closestbeamcenter == n);
if (user_in_beam == 0)
user_in_beam_random = 0;
else
user_in_beam_random = user_in_beam(randperm(numel(user_in_beam),1));
superuser_location_in_beam(n,![]() = user_location(user_in_beam_random,:);
= user_location(user_in_beam_random,:);
end
end
% randomly select one of the users accessing the nth beam
%superuser_location_in_beam = zeros(N, 2);
% for n = 1:N
% user_in_beam = find(closestbeamcenter == n);
% if isempty(user_in_beam)
% superuser_location_in_beam(n,![]() = [0,0];
= [0,0];
% else
% k = randperm(length(user_in_beam),1);
% superuser_location_in_beam(n,![]() = user_location(user_in_beam(k),:);
= user_location(user_in_beam(k),:);
% end
% end
% channel coefficient
h = zeros(N,N);
for n = 1:N
for nn = 1:N
h(n,nn) = sqrt(GRG) lamda/(4*pi * distance_sky2ground(superuser_location_in_beam(n,:), satellite_location));
end
end
g = abs(h).^2;
%draw
draw_mapping (satellite_location, beamcenter_location, superuser_location_in_beam)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Start iteration %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% initial iteration
beta = 1;
q_previous = ones(N,1) * sqrt(Ptotal/(N*Btot));
GAMMA_previous = ones(N,1);
for n = 1:N
GAMMA_previous(n) = g(n,n) * q_previous(n).^2 / (interference_baseline(q_previous,g,n) + N0);
end
%
while true
cvx_begin
variables s(N) T q(N) GAMMA(N)
minimize( 1 + (Btot/Ptotal)*sum_square(q) + Btot*sum(s) - beta*Btot*T )
subject to
% L1
for n = 1:N
GAMMA(n) >= SINR_min;
end
%L2
sum(q.^2) <= T*Ptotal;
%L3
for n = 1:N
q(n).^2 <= T*Pmax;
end
% L4
1 <= T * Btot;
% L5
1 >= T * Bc;
% L6
for n=1:N
q(n) >= 0;
end
% L7.1
for n = 1:N
T - log(1 + (GAMMA(n))/log(2))/demand_in_beam(n) <= s(n);
%T- (1/demand_in_beam(n)) * log2(1 + GAMMA(n)) <= s(n);
end
% L7.3
for n = 1:N
interference1 = 0;
for n1 = 1:N
if n1 ~= n
interference1 = interference1 + q(n).^2 * g(n, n1); %interference power
end
end
interference1 + N0 + (g(n,n)*(q_previous(n).^2)*GAMMA(n))/(GAMMA_previous(n).^2)-2*(g(n,n)*q_previous(n)*q(n))/(GAMMA_previous(n))<= 0;
end
% L8
for n = 1:N
s(n) >= 0;
end
cvx_end
q_previous = q;
GAMMA_previous = GAMMA;
beta = (1/Btot + 1/Ptotal * sum(q.^2) + sum(s))/T;
f1 = 0;
for n = 1:N
f1 = f1 + sum(abs( g(n,n)*(q_previous(n).^2)*GAMMA(n)/(GAMMA_previous(n).^2) ...
-g(n,n)*q_previous(n)*q(n)/GAMMA_previous(n) ));
end
f2 = abs(1 + Btot/Ptotal*sum(q.^2) + Btot*sum(s) - beta*Btot*T);
if f1 <= 1e-4 && f2 <= 1e-4
break
end
end
B_opt = 1 / T;
p_opt = B_opt*(q.^2);
Successive approximation method to be employed.
For improved efficiency, SDPT3 is solving the dual problem.
SDPT3 will be called several times to refine the solution.
Original size: 236 variables, 79 equality constraints
7 exponentials add 56 variables, 35 equality constraints
Cones | Errors |
Mov/Act | Centering Exp cone Poly cone | Status
--------±--------------------------------±--------
7/ 7 | 5.601e+00 6.651e+00 0.000e+00 | Inaccurate/Solved
7/ 7 | 4.080e+00 2.424e+00 0.000e+00 | Inaccurate/Solved
7/ 7 | 1.884e+00 3.896e-01 0.000e+00 | Inaccurate/Solved
3/ 3 | 4.616e-01 1.004e-02 0.000e+00 | Inaccurate/Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Inaccurate/Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Inaccurate/Solved
0/ 0 | 0.000e+00 0.000e+00 0.000e+00 | Inaccurate/Solved
Status: Inaccurate/Solved
Optimal value (cvx_optval): -87.2218
this the result
close all
clear
%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Fixed parameters %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
satellite_location = [13 0]; %point A below star
%beamcenter_location = [114.14 22.02; 120.38 22.48; 107.32 27.4; 114.17 28.56; 120.86 28.11; 108.86 34; 116.191 33.571]; %beam center coordinates
%beamcenter_location = [114.14 22.02 120.38 22.48 107.32 27.4 114.17 28.56 120.86 28.11 108.86 34 116.191 33.571 110.5 23.7 118.9 34.1 123.3 25.2 106.6 26.8 98.7 18.4 105.8 27.7 109.4 27.8 101.0 22.0 97.8 21.3 104.7 30.7 115.2 27.1 98.0 25.7 111.1 29.7 118.7 24.9 120.0 36.1 121.2 31.3 99.8 21.3 117.7 34.4 112.1 27.3 98.1 26.3 110.3 28.6 112.1 24.5 113.9 26.5 118.9 24.5 98.8 24.2 103.7 23.0 120.9 31.4 106.5 23.8 107.6 30.4 112.1 23.5 115.6 34.3 117.5 36.2 118.9 25.8 120.3 33.0 106.6 26.0 112.7 28.3 119.6 27.6 121.2 31.2 99.6 20.9 103.9 23.5 109.6 28.8 110.4 22.4 111.6 33.6 115.5 31.3 116.4 27.4 118.4 29.1 119.3 31.3 120.7 33.0 121.9 25.0 104.0 30.7 106.8 28.2 113.7 24.9 118.0 27.3 118.2 30.7 120.2 28.9 121.7 25.1];
beamcenter_location =[16.37 48.20;11.58 48.14; 17.70 53.97; 12.49 41.89; 15.99 45.81; 13.41 52.51;12.56 55.68];
N = size(beamcenter_location, 1) % number of beams,number of row read
M = 12; %number of ground station
B1 = 11.7 * 1e9; % lower bound of available bandwidth
B2 = 12.2 * 1e9; % upper bound of available bandwidth Hz
Btot =B2-B1; % total carrier width
% SINR_min_dB = -5.23;
SINR_min_dB = -2.2;
SINR_min = 10^(SINR_min_dB/10); % 0.3
Bc = 5e6; % minimum bandwidth(Hz)
N0_dB = -204; % Bottom Noise dBW / Hz
N0 = 10^(N0_dB/10);
G_dB = 52; % Maximum beam gain (51.8dBi)
G = 10^(G_dB/10);
GR_dB = 39.8;
GR = 10^(GR_dB/10); % user antenna gain(39.8dBi)
Ptotal = 1000; % Total avaiable transmit power(W)
Pmax = 100; % Maximum power beam(W)
lamda = 3e8 / (11.951e9); % Wavelength (m)
demand_mean = 300; % Average of demand1e6 (bps)(bps)
%%%%%%%%%%%%%%%%%%%%%%%%% random ground station locations, user requirments %%%%%%%%%%%%%%%%%%%%%%%%
% import polygon vertex coordinates
%tx = xlsread(‘cell.xlsx’);
%xx = tx(:,1);
%yy = tx(:,2);
% random distribution, the specified number points
%user_location = zeros(M,2);
%n = 1;
%while (n <= M)
%xp = 100+30rand;
%yp = 18+20rand;
%if inpolygon(xp,yp,xx,yy)
%user_location(n,1) = xp;
%user_location(n,2) = yp;
%n = n+1;
%end
%end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Fixed Earth Station Position %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%user_location =[16.78 49.73;11.61 48.18;15.12 45.32;13.71 53.44;12.51 41.81;17.46 52.42;14.06 47.10;15.62 50.55;13.90 58.74;12.45 41.87]
user_location =[16.78 49.73;12.85 45.61;11.61 48.18;15.12 45.32;13.71 53.44;12.56 41.86;12.51 41.81;17.46 52.42;14.06 47.10;15.62 50.55;13.90 58.74;11.99 48.81;12.45 41.87]
% normal distribution of random user demand
demand = normrnd(demand_mean, 50, M, 1)1e6 ; % user requirements bps, the total amount of reources that seven beam can provide is 4.031e9(bps)
for m = 1:M
if demand(m) < 0
demand(m) = 1e6;
end
end
%%%%%%%%%%%%%%%%%%%%%%% convert a plurality of user within a beam into a %%%%%%%%%%%%%%%%%%%%%
distance_userandbeam = zeros(M, N);
closestbeamcenter = zeros(M, 1); % give the intial value of a by distance
demand_in_beam = zeros(N, 1); % sum of all user requirment within the beam
% is the approximate user requirment
for m = 1:M
for n = 1:N
distance_userandbeam(m,n) = distance_sky2ground(user_location(m,:), beamcenter_location(n,:));
end
% The nearest beam to the mth user is closestbeamcenter(m)
closestbeamcenter(m) = find(distance_userandbeam(m,![]() == min(distance_userandbeam(m,:)), 1);
== min(distance_userandbeam(m,:)), 1);
end
% generate approximate user
for m = 1:M
for n = 1:N
if (closestbeamcenter(m) == n)
demand_in_beam(n) = demand_in_beam(n) + demand(m);
end
end
end
% randomly select one of the users accessing the nth beam
superuser_location_in_beam = zeros(N, 2);
for n = 1:N
user_in_beam = find(closestbeamcenter == n);
if (user_in_beam == 0)
user_in_beam_random = 0;
else
user_in_beam_random = user_in_beam(randperm(numel(user_in_beam),1));
superuser_location_in_beam(n,![]() = user_location(user_in_beam_random,:);
= user_location(user_in_beam_random,:);
end
end
% randomly select one of the users accessing the nth beam
%superuser_location_in_beam = zeros(N, 2);
% for n = 1:N
% user_in_beam = find(closestbeamcenter == n);
% if isempty(user_in_beam)
% superuser_location_in_beam(n,![]() = [0,0];
= [0,0];
% else
% k = randperm(length(user_in_beam),1);
% superuser_location_in_beam(n,![]() = user_location(user_in_beam(k),:);
= user_location(user_in_beam(k),:);
% end
% end
% channel coefficient
h = zeros(N,N);
for n = 1:N
for nn = 1:N
h(n,nn) = sqrt(GRG) lamda/(4*pi * distance_sky2ground(superuser_location_in_beam(n,:), satellite_location));
end
end
g = abs(h).^2;
%draw
draw_mapping (satellite_location, beamcenter_location, superuser_location_in_beam)
%%%%%%%%%%%%%%%%%%%%%%%%%%%%% Start iteration %%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% initial iteration
beta = 1;
q_previous = ones(N,1) * sqrt(Ptotal/(N*Btot));
GAMMA_previous = ones(N,1);
for n = 1:N
GAMMA_previous(n) = g(n,n) * q_previous(n).^2 / (interference_baseline(q_previous,g,n) + N0);
end
%
while true
cvx_begin
variables s(N) T q(N) GAMMA(N)
minimize( 1 + (Btot/Ptotal)*sum_square(q) + Btot*sum(s) - beta*Btot*T )
subject to
% L1
for n = 1:N
GAMMA(n) >= SINR_min;
end
%L2
sum(q.^2) <= T*Ptotal;
%L3
for n = 1:N
q(n).^2 <= T*Pmax;
end
% L4
1 <= T * Btot;
% L5
1 >= T * Bc;
% L6
for n=1:N
q(n) >= 0;
end
% L7.1
for n = 1:N
T - log(1 + (GAMMA(n))/log(2))/demand_in_beam(n) <= s(n);
%T- (1/demand_in_beam(n)) * log2(1 + GAMMA(n)) <= s(n);
end
% L7.3
for n = 1:N
interference1 = 0;
for n1 = 1:N
if n1 ~= n
interference1 = interference1 + q(n).^2 * g(n, n1); %interference power
end
end
interference1 + N0 + (g(n,n)*(q_previous(n).^2)*GAMMA(n))/(GAMMA_previous(n).^2)-2*(g(n,n)*q_previous(n)*q(n))/(GAMMA_previous(n))<= 0;
end
% L8
for n = 1:N
s(n) >= 0;
end
cvx_end
q_previous = q;
GAMMA_previous = GAMMA;
beta = (1/Btot + 1/Ptotal * sum(q.^2) + sum(s))/T;
f1 = 0;
for n = 1:N
f1 = f1 + sum(abs( g(n,n)*(q_previous(n).^2)*GAMMA(n)/(GAMMA_previous(n).^2) ...
-g(n,n)*q_previous(n)*q(n)/GAMMA_previous(n) ));
end
f2 = abs(1 + Btot/Ptotal*sum(q.^2) + Btot*sum(s) - beta*Btot*T);
if f1 <= 1e-4 && f2 <= 1e-4
break
end
end
B_opt = 1 / T;
p_opt = B_opt*(q.^2);
this the code
-
Numbers such as 12 e9 are terrible scaling, and may cause difficulties… Try to change the units used in your problem to avoid this.
-
If you have Mosek available as solver, use it. Otherwise follow the instructions at CVXQUAD: How to use CVXQUAD's Pade Approximant instead of CVX's unreliable Successive Approximation for GP mode, log, exp, entr, rel_entr, kl_div, log_det, det_rootn, exponential cone. CVXQUAD's Quantum (Matrix) Entropy & Matrix Log related functions
-
Use of SCA can lead to wilder and wilder solutions, and therefore input data to the next iteration. At some point, the solver might fail, even if the steps in (1) and (2) are followed.
https://twitter.com/themarklstone/status/1586795881168265216
Items 1 and 3 in my post still apply.
yes, I applied both 1 and 3.
How did you apply 1 and 3? If you applied 3, you wouldn’t even be running that code.
sorry, I am saying I applied 1 and 2
Please show your program after you applied 1.
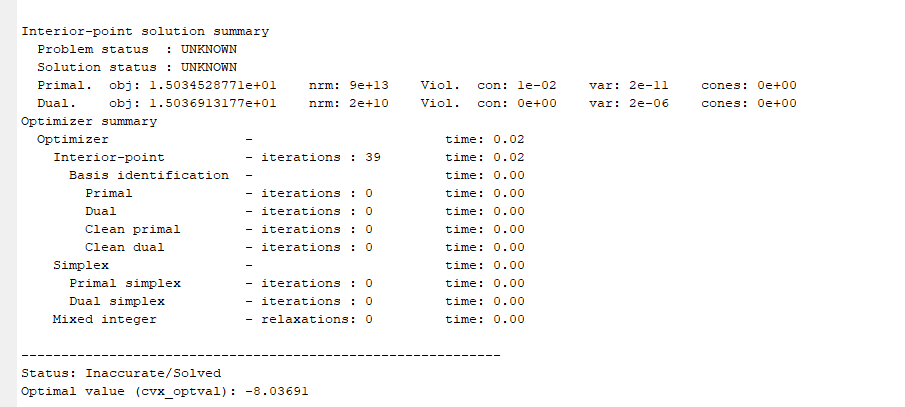
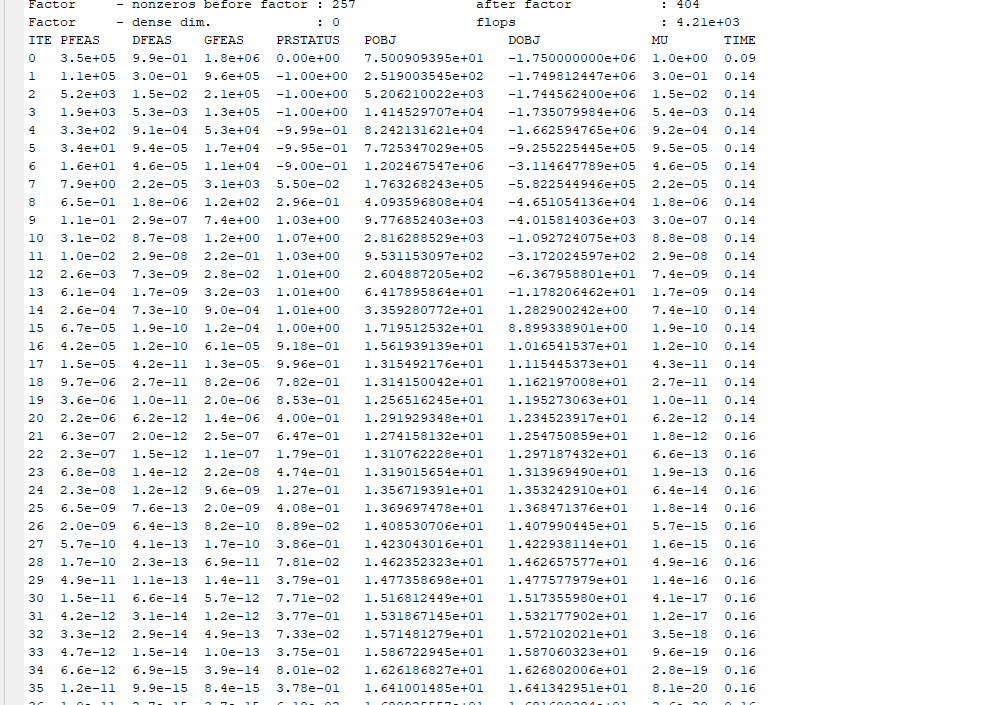
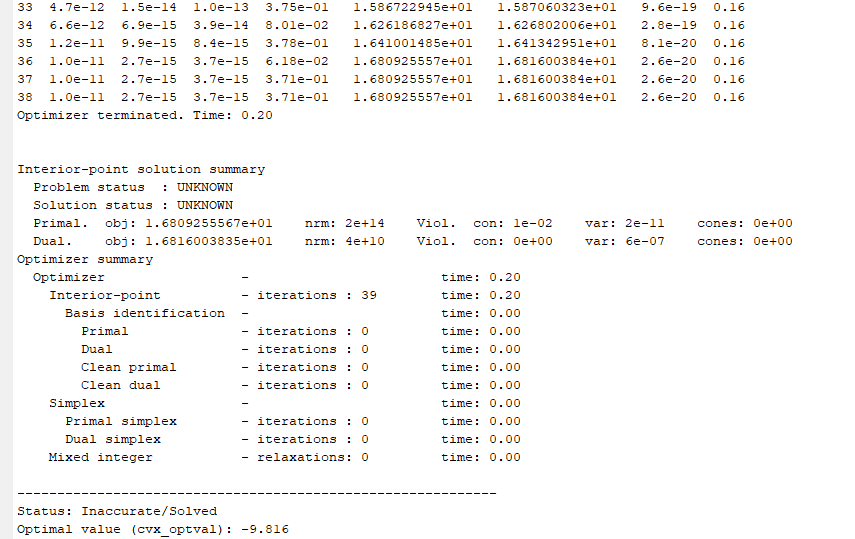
Did the first iteration of SCA, i.e., the first CVX problem solve to reported optimality? if not, you likely didn’t scale well enough. If the first problem solved to otimality but a subsequent problem did not, then you appear to have encountered the unreliability and inadequacy of unsafeguarded SCA … wilder and wilder solutions to subproblems and hence inputs, until on some iteration, the solver fails.
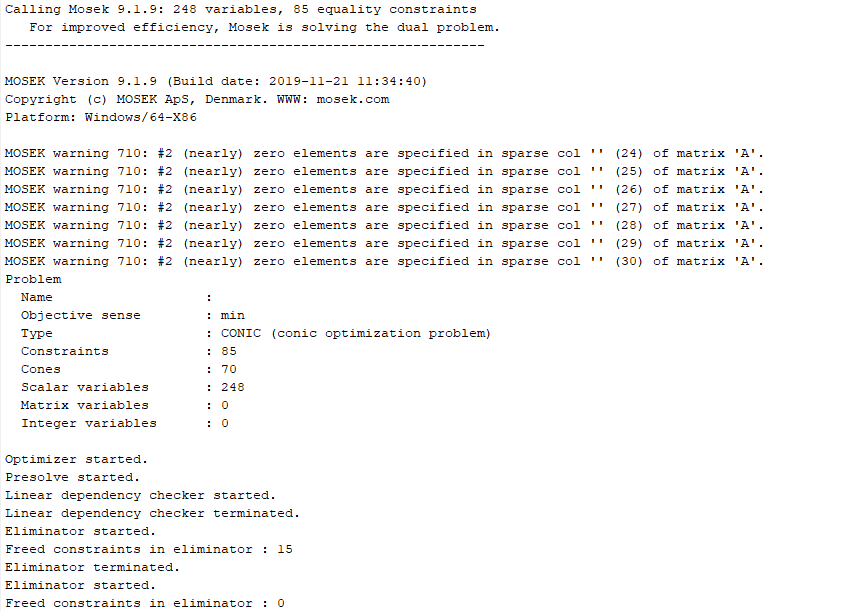
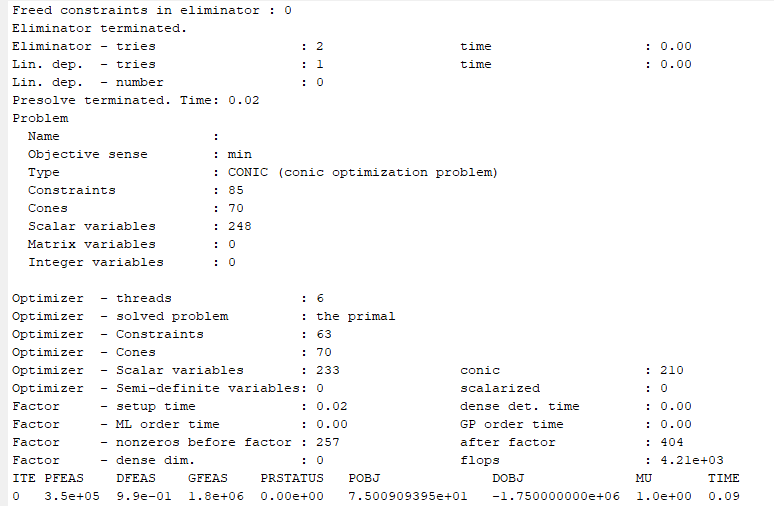
Is that output from the first iteration? In any event, you have not shown us your program, with input data, after the numerical scaling you have supposedly performed. And show us all the Mosek output, including the portion before the iteration lines. Are there any warning messages from Mosek?
The Mosek warnings tell you there are near zero input data. That means the numerical scaling is terrible. So you need to follow step 1, and change units or do something else so that there will not be near zero input data.
okay I will change it
I changed the units it is still the same.