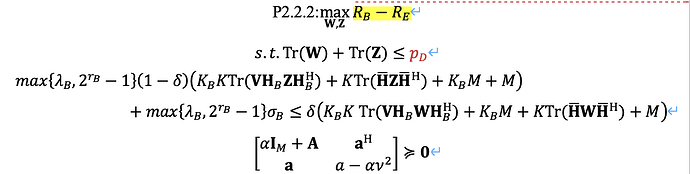Question on BCD in cvx

1

I am currently using the BCD algorith. In my previous subproblem, I optimized and obtained the variable R_B,R_E,lambda_B, lambda_E, xi, alpha1, beta1and V. In the current subproblem, given the optimized variable mentioned above, I want to optimize the variable W and Z. However, is it feasible to optimize the variable W and Z (both are hermitian semidefinite) with the target function given constant R_B - R_E? Additionally, even if I define R_B,R_E as variables, the maximum secrecy rate obtained through optimization is at most R_B - R_E from the optimization result in the previous subproblem. These two questions have been troubling me for a long time. Please help me!

This is my current subproblem:

Screenshot 2024-01-03 at 10.24.28
Screenshot 2024-01-03 at 10.24.281390×352 36.4 KB

This is my cvx code:

%% %%%%%%%%%% Given R_B,R_E,lambda_B,lambda_E,xi,alpha1,beta1and V, optimize W,Z %%%%%%%%%%
load Parameter20240102-2.all.mat % optimized R_B,R_E,lambda_B,lambda_E,xi,alpha1,beta1and V in the last sub-problem

RE_l = R_Eve;
TTP1 = [0]; tmp = 0; flag_1 = 0; idx_1 = 0;
while(flag_1 == 0)
    cvx_begin
    cvx_solver mosek
    cvx_precision low
    variables R_B R_E;
    variable W(N,N) hermitian semidefinite;
    variable Z(N,N) hermitian semidefinite;

    expression mu;
    expressions a11 a12 a21 a22 A;
    % LHS Taylor expression
    %mu = real(2^RE_l + 2^RE_l*log(2)*(R_E - RE_l));
    mu = 2^RE_l + 2^RE_l*log(2)*(R_E - RE_l);

    a11 = alpha1.*diag(ones(M, 1)) + lambda_E.*K_E.*K.*diag(diag(H_LOS*Z*H_LOS'))*V -...
        K_E.*K.*diag(diag(H_LOS*W*H_LOS'))*V;
    %a11 = real(a11);

    a12 = (lambda_E.*K_E.*K.*g_hat*diag(diag(H_LOS*Z*H_LOS'))*V - ...
        K_E.*K.*g_hat*diag(diag(H_LOS*W*H_LOS'))*V)';
    %a12 = real(a12);

    a21 = lambda_E.*K_E.*K.*g_hat*diag(diag(H_LOS*Z*H_LOS'))*V - ...
        K_E.*K.*g_hat*diag(diag(H_LOS*W*H_LOS'))*V;
    %a21 = real(a21);

    a22 = (lambda_E.*K_E.*K.*real(trace(V*G_hat*Z*G_hat')) -...
        K_E.*K.*real(trace(V*G_hat*W*G_hat')) +...
        lambda_E.*K.*real(trace(H_LOS*Z*H_LOS')) -...
        K.*real(trace(H_LOS*W*H_LOS')) +...
        lambda_E*K_E*M*real(trace(Z)) + lambda_E*M*real(trace(Z)) -...
        K_E*M*real(trace(W)) - M*real(trace(W)) - xi) - alpha1.*nu^2;
    %a22 = real(a22);

    A = [a11, a12; a21, a22];

    % objective function
    maximize (R_B - R_E)
    %maximize (trace(W) + trace(Z))
    % Constraints
    subject to
    % Constraint 1
    exp(log(2)*R_B) <= lambda_B + 1;
    % Constraint 2
    mu >= lambda_E + 1;
    % Constraint 3
    trace(W) + trace(Z) <= p_D;
    % Constraint 4
    
    max(lambda_B, 2^r_B - 1).*(K_B*K*real(trace(V*H_B*Z*H_B')) + K_B*M*real(trace(Z)) +...
        K*real(trace(H_LOS*Z*H_LOS')) + M*real(trace(Z)) + sigma_B) <=...
        K_B*K*real(trace(V*H_B*W*H_B')) + K_B*M*real(trace(W)) +...
        K*real(trace(H_LOS*W*H_LOS')) + M*real(trace(W));
    
    % Constraint 5
    %A == semidefinite(M + 1);
    A == hermitian_semidefinite(M + 1);

    cvx_end

    % update
    RE_l = R_E;
    tmpN = R_B - R_E;
    TTP1 = [TTP1 tmpN];
    % convergence
    if abs(tmpN - tmp)/abs(tmp) < 10^(-2)
        flag_1 = 1;
        break;
    end
    tmp = tmpN;
    % maximum loop
    idx_1 = idx_1 + 1;
    if idx_1 >= 30
        break;
    end
end
2

Please be clearer as to exactly where you need assistance.

Is each CVX problem (instance) accepted by CVX without error message?
Is each CVX problem (instance) getting solved to reported optimality, and not resulting in CVX declaring it “infeasibile”, or “unbounded”, or (solver failed due to) numerical difficulties or UNKNOWN?

You should remove cvx_precision low, i.e., leave cvx_precision art its default setting.

Not every (crazy) iterative scheme calling CVX to solve an iterative series of subproblems works. Most attempts posted on this forum don’t work reliably, or at all (posts from 2012 by @stephen_boyd being a notable exception). Although I suppose it is a biased sample, because the people who do have success don’t tend to post here asking for help.

If the answers to both of these question is yes, do you have nay analysis which shows that your overall algorithm will (should) converge to the correct answer of your problem?

The following may or may not be relevant to your problem: