I want to convexity the third and the fourth constraints which have quadratic terms in x.
What are the barred u_i’s ?
There are multiple non-convex-looking things in the 3rd and 4th constraints (having z as a multiplicative factor on the quadratic term in x (even if a >= 0), not to mention the RHS), so I don’t think it’s just a matter of changing how they are entered. Do you wish to change the constraints to different, i.e., non-equivalent, constraints, which therefore make the optimization problem different than the one you entered? If so, that opens up an unlimited number of possibilities.
Yes a >0. I think of fixing x, then the constraints will be convex. After that I do one-dimensional search over x (x=0:.1:1) to find the optimal value of x. But this is computational heavy. So even you change the constraints to equivalents ones, I think, I still will get near-optimal value of the objective function.
You still haven’t said what the u_i bars are. If they are constants, then fine. If they are variables, then the right-hand sides of the 3rd and 4th constraints are not convex, even if x is held constant.
What are the barred is constant, it is the initial value of Taylor approximation of the exponential term. This an iterative program.
The constraints without Taylor approximation are
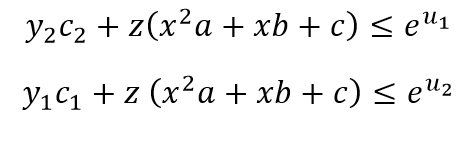
Please read the FAQ. You seem to be working with CVX as if it is a general purpose optimization modeling tool, and it’s not that at all.
