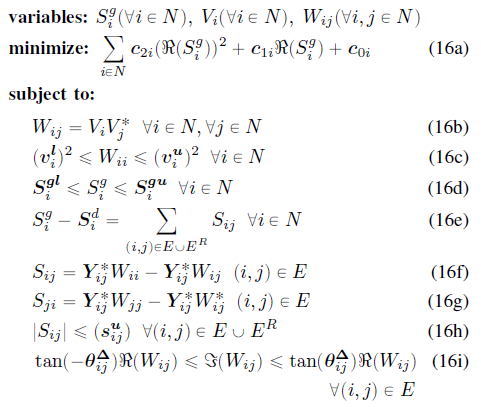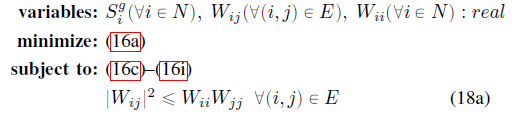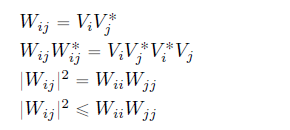hi,
I am trying to implement the product of complex numbers in CVX. However, only scalar quadratic forms are allowed in CVX. Any suggestions How I can implement the following product:
((Voltage) * (Voltage)’ * Y);
Voltage is a 3*1 complex vector.
Y is a 3x3 complex Matrix.
Thanks
You haven’t said whether Y is Hermitian semidefinite. But let me afford you every benefit by assuming that Y is the identity matrix. Then your resulting 3 by 3 matrix, ((Voltage) * (Voltage)’ * Y) has (i,j) element being a product of variables, Voltage(i)*Voltage(j), and those elements are non-convex for the off-diagonal elements (i.e., i \ne j).
Thanks for your response, Mark. You are right. In fact, I am only interested in the diagonal elements of the product in my model. I am using something like this in my code. PF=diag((Voltage)*(Voltage)'*Y); But the problem is I am not finding any way to get the product of two voltages. The product of voltages is also involved in some other parts of my optimization model as well. It’s a code for running AC OPF using SOCP.
What properties of Y make those diagonal elements of ((Voltage) * (Voltage)’ * Y) convex (or concave)? The first thing you need to to is to prove your optimization problem is convex, as is described in the link I provided.
It’s a well-known and well-proved convex problem after some relaxations to non-convexities. I am implementing a model from a published paper.
You haven;t shown us the full problem you are trying to implement in CVX. You haven’t shown us the proof it is convex. We don’t even know what Y or its properties are.
When you have a complete specification of the convex optimization problem, as well as a proof that (version of) the problem is convex, if you are still having trouble implementing it in CVX, please let us know where your difficulties are. But before doing that, please read the link very carefully, and take it to heart.
Mark, I am really grateful for the time you are taking to respond to my queries.
Previously, I solved my models with heuristic algorithms and now I am trying to implement my new models in CVX but before that, I am trying to reproduce some of the already published results to see what I can do with CVX.
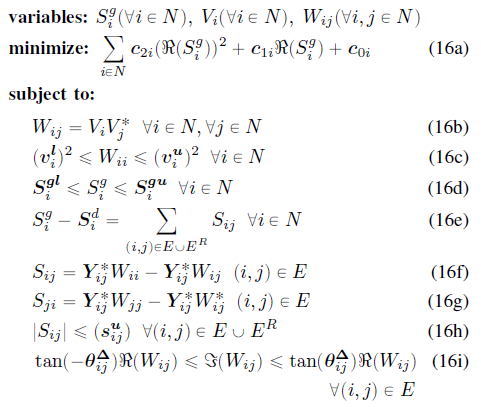
This above model has a non-convex constraint 16b. so it has been convexified in the model below:
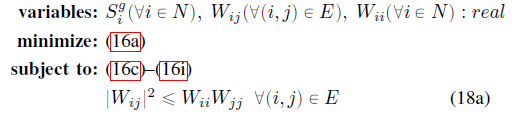
The discussions and proof of optimality for ACOPF using SOC are available in several papers.
For each ( i,j) \in E, (18a) is a rotated second order cone constraint, which can be implemented in CVX as
{W(i,j),W(i,i),W(j,j)} == rotated_complex_lorentz(1)
This will enforce W(i,i) >= 0, W(j,j) >= 0.
http://cvxr.com/cvx/doc/funcref.html#sets
Can you implement the rest of the model in CVX?
1 Like
Actually not because the biggest problem is obtaining these Ws as they are:
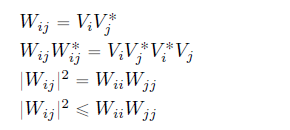
Ws themselves involve products of voltages.
Isn’t the point of the convexifyng relaxation into rotated second order cones that you use those instead of the product equality formulation? As to whether the solution to the relaxed problem satisfies those equalities, and what to do if they are not, I presume that is addressed in the paper(s).
It only convexifies/relaxes 16b. We have other constraints as well that use products of voltages such as 16f and 16g.
Where does it say that Y_{ij}^* is an optimization variable? I presumed that is input data; therefore, (16f) and (16g) are affine. Maybe you need to carefully re-read the papers, so that you really understand them; and that includes understanding what is input data vs optimization variables.
1 Like
Yes, You are right. It’s a constant matrix of line admittances. Variables are clearly written at the top of the optimization problem. I have got your point. Many thanks for your help Mark.
Yes, I saw the variable list, and I presumed you had as well.
1 Like
Your hint of affine helped a lot. Otherwise, I was lost by complex multiplication.