Problems encountered in solving a quadratic programming problem

1

Hi all,

I’m having a problem solving a quadratic programming problem with the following background: I approximated a single pendulum model to a linear model based on Koopman operator, and then based on that model, I solved a quadratic programming problem with kkt condition, and the goal is to get this pendulum upright and balanced (x0=[0;0], xf=[pi;0]), cost is energy optimal. The problem is: 1. The problem is: 1. if I set xf to [pi;0] and the optimisation time to 2 seconds, the result is wrong, if I set the optimisation time to 0.5 seconds, the answer is right again; 2. if I set xf to [pi/3;0], the answer is right no matter what the optimisation time is, the bigger the angle of the end point is, the more wrong the answer is, and it is basically wrong after exceeding pi/2. I hope you can help to analyse it, thanks!

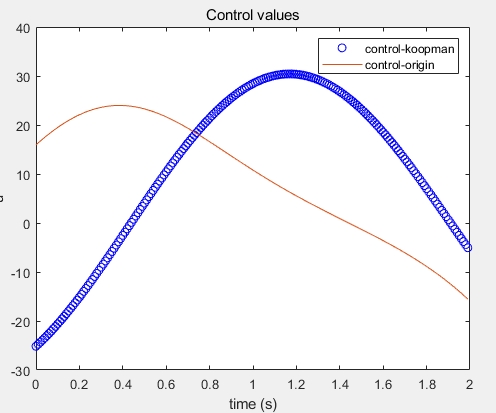
end angle is 2pi，optimization time is 2s
Fig1. end angle is 2pi，optimization time is 2s

2

This is not presented as a CVX problem.

it appears you have math modeling concerns. Therefore, https://math.stackexchange.com/ or some other site might be more appropriate, unless you present a specific convex optimization model and any CVX implementation or solution concerns.